Often, one would be interested in finding the probability of the occurrence of a set of random variables when other random variables in the problem are held fixed. As an example of population health study, one would be interested in finding what is the probability of a person, in the age range 40-50, developing heart disease with high blood pressure and diabetes. Questions such as these can be modeled using conditional probability, which is defined as the probability of an event, given that another event has happened. More formally, if we take the variables A and B, this definition can be rewritten as follows:
Similarly:
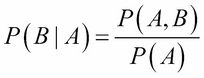
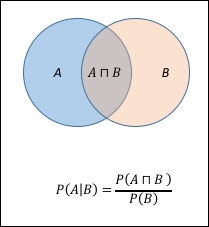
The following Venn diagram explains the concept more clearly:
In Bayesian inference, we are interested in conditional probabilities corresponding to multivariate distributions. If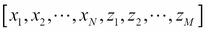 
denotes the entire random variable set, then the conditional probability of 
, given that 
is fixed at some value, is given by the ratio of joint probability of 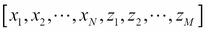and joint probability of :
In the case of two-dimensional normal distribution, the conditional probability of interest is as follows:
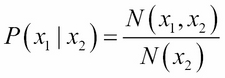
It can be shown that (exercise 2 in the Exercises section of this chapter) the RHS can be simplified, resulting in an expression for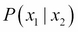 
in the form of a normal distribution again with the mean 
and variance 
.
