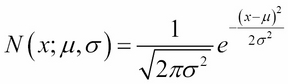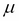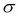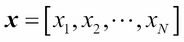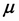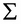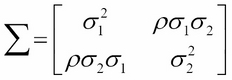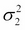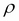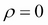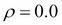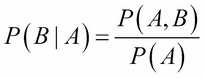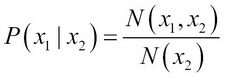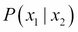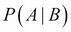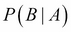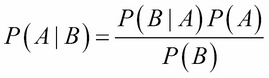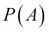Probability distributions
In both classical and Bayesian approaches, a probability distribution function is the central quantity, which captures all of the information about the relationship between variables in the presence of uncertainty. A probability distribution assigns a probability value to each measurable subset of outcomes of a random experiment. The variable involved could be discrete or continuous, and univariate or multivariate. Although people use slightly different terminologies, the commonly used probability distributions for the different types of random variables are as follows:
Probability mass function (pmf) for discrete numerical random variables
Categorical distribution for categorical random variables
Probability density function (pdf) for continuous random variables
One of the well-known distribution functions is the normal or Gaussian distribution, which is named after Carl Friedrich Gauss, a famous German mathematician and physicist. It is also known by the name bell curve because of its shape. The mathematical form of this distribution is given by:
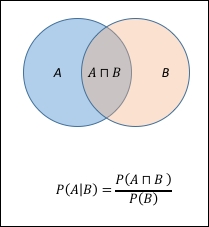
Here, 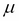 is the mean or location parameter and
is the mean or location parameter and 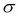 is the standard deviation or scale parameter (
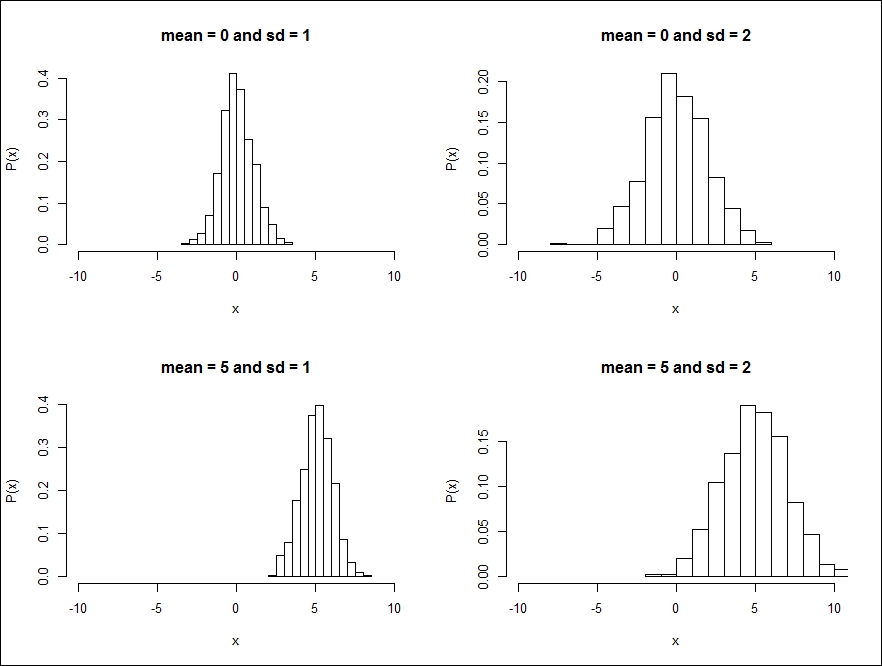
is the standard deviation or scale parameter ( is called variance). The following graphs show what the distribution looks like for different values of location and scale parameters:
is called variance). The following graphs show what the distribution looks like for different values of location and scale parameters:
One can see that as the mean changes, the location of the peak of the distribution changes. Similarly, when the standard deviation changes, the width of the distribution also changes.
Many natural datasets follow normal distribution because, according to the
central limit theorem, any random variable that can be composed as a mean of independent random variables will have a normal distribution. This is irrespective of the form of the distribution of this random variable, as long as they have finite mean and variance and all are drawn from the same original distribution. A normal distribution is also very popular among data scientists because in many statistical inferences, theoretical results can be derived if the underlying distribution is normal.
Now, let us look at the multidimensional version of normal distribution. If the random variable is an N-dimensional vector, x is denoted by:
Then, the corresponding normal distribution is given by:
Here, 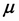 corresponds to the mean (also called location) and
corresponds to the mean (also called location) and 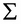 is an N x N covariance matrix (also called scale).
is an N x N covariance matrix (also called scale).
To get a better understanding of the multidimensional normal distribution, let us take the case of two dimensions. In this case,  and the covariance matrix is given by:
and the covariance matrix is given by:
Here,  and
and 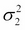 are the variances along
are the variances along  and
and  directions, and
directions, and 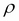 is the correlation between
is the correlation between  and
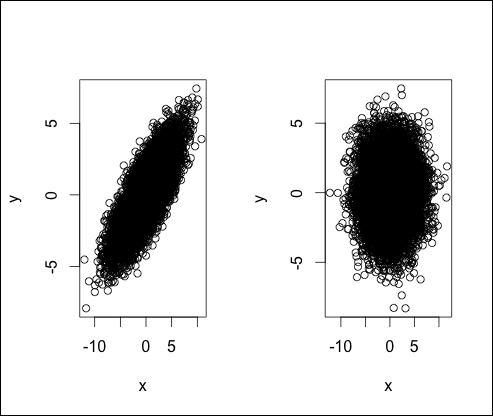
and  . A plot of two-dimensional normal distribution for
. A plot of two-dimensional normal distribution for  ,
,  , and
, and  is shown in the following image:
is shown in the following image:
If 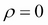 , then the two-dimensional normal distribution will be reduced to the product of two one-dimensional normal distributions, since
, then the two-dimensional normal distribution will be reduced to the product of two one-dimensional normal distributions, since 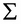 would become diagonal in this case. The following 2D projections of normal distribution for the same values of
would become diagonal in this case. The following 2D projections of normal distribution for the same values of  and
and 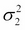 but with
but with  and
and 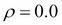 illustrate this case:
illustrate this case:
The high correlation between x and y in the first case forces most of the data points along the 45 degree line and makes the distribution more anisotropic; whereas, in the second case, when the correlation is zero, the distribution is more isotropic.
We will briefly review some of the other well-known distributions used in Bayesian inference here.
 Argentina
Argentina
 Australia
Australia
 Austria
Austria
 Belgium
Belgium
 Brazil
Brazil
 Bulgaria
Bulgaria
 Canada
Canada
 Chile
Chile
 Colombia
Colombia
 Cyprus
Cyprus
 Czechia
Czechia
 Denmark
Denmark
 Ecuador
Ecuador
 Egypt
Egypt
 Estonia
Estonia
 Finland
Finland
 France
France
 Germany
Germany
 Great Britain
Great Britain
 Greece
Greece
 Hungary
Hungary
 India
India
 Indonesia
Indonesia
 Ireland
Ireland
 Italy
Italy
 Japan
Japan
 Latvia
Latvia
 Lithuania
Lithuania
 Luxembourg
Luxembourg
 Malaysia
Malaysia
 Malta
Malta
 Mexico
Mexico
 Netherlands
Netherlands
 New Zealand
New Zealand
 Norway
Norway
 Philippines
Philippines
 Poland
Poland
 Portugal
Portugal
 Romania
Romania
 Russia
Russia
 Singapore
Singapore
 Slovakia
Slovakia
 Slovenia
Slovenia
 South Africa
South Africa
 South Korea
South Korea
 Spain
Spain
 Sweden
Sweden
 Switzerland
Switzerland
 Taiwan
Taiwan
 Thailand
Thailand
 Turkey
Turkey
 Ukraine
Ukraine
 United States
United States