Calculus and Differential Equations

In this chapter, we will discuss various topics related to calculus. Calculus is the branch of mathematics that concerns the processes of differentiation and integration. Geometrically, the derivative of a function represents the gradient of the curve of the function, and the integral of a function represents the area below the curve of the function. Of course, these characterizations only hold in certain circumstances, but they provide a reasonable foundation for this chapter.

We’ll start by looking at calculus for a simple class of functions: polynomials. In the first recipe, we’ll create a class that represents a polynomial and define methods that differentiate and integrate the polynomial. Polynomials are convenient because the derivative or integral of a polynomial is again a polynomial. Then, we’ll use the SymPy package to perform symbolic differentiation and integration on more general functions. After that, we’...

Technical requirements

In addition to the scientific Python packages NumPy and SciPy, we also need the SymPy, JAX, and diffrax packages. These can be installed using your favorite package manager, such as pip:

python3.10 -m pip install sympy jaxlib jax sympy diffrax

There are different options for the way you install JAX. Please see the official documentation for more details: https://github.com/google/jax#installation.

The code for this chapter can be found in the Chapter 03 folder of the GitHub repository at https://github.com/PacktPublishing/Applying-Math-with-Python-2nd-Edition/tree/main/Chapter%2003.

Primer on calculus

Calculus is the study of functions and the way that they change. There are two major processes in calculus: differentiation and integration. Differentiation takes a function and produces a new function—called the derivative—that is the best linear approximation at each point. (You may see this described as the gradient of the function. Integration is often described as anti-differentiation—indeed, differentiating the integral of a function does give back the original function—but is also an abstract description of the area between the graph of the function and the axis, taking into account where the curve is above or below the axis.

Abstractly, the derivative of a function at a point is defined as a limit (which we won’t describe here) of the quantity:

This is because this small number becomes smaller and smaller. This is the difference in divided by the difference in , which is why the derivative...

Working with polynomials and calculus

Polynomials are among the simplest functions in mathematics and are defined as a sum:

Here, represents a placeholder to be substituted (an indeterminate), and is a number. Since polynomials are simple, they provide an excellent means for a brief introduction to calculus.

In this recipe, we will define a simple class that represents a polynomial and write methods for this class to perform differentiation and integration.

Getting ready

There are no additional packages required for this recipe.

How to do it...

The following steps describe how to create a class representing a polynomial, and implement differentiation and integration methods for this class:

1. Let’s start by defining a simple class to represent a polynomial:

   class Polynomial:

       """Basic polynomial class"""

       def __init__(self, coeffs):

       ...

Differentiating and integrating symbolically using SymPy

At some point, you may have to differentiate a function that is not a simple polynomial, and you may need to do this in some kind of automated fashion—for example, if you are writing software for education. The Python scientific stack includes a package called SymPy, which allows us to create and manipulate symbolic mathematical expressions within Python. In particular, SymPy can perform differentiation and integration of symbolic functions, just like a mathematician.

In this recipe, we will create a symbolic function and then differentiate and integrate this function using the SymPy library.

Getting ready

Unlike some of the other scientific Python packages, there does not seem to be a standard alias under which SymPy is imported in the literature. Instead, the documentation uses a star import at several points, which is not in line with the PEP8 style guide. This is possibly to make the mathematical expressions...

Solving equations

Many mathematical problems eventually reduce to solving an equation of the form , where is a function of a single variable. Here, we try to find a value of for which the equation holds. The values of for which the equation holds are sometimes called roots of the equation. There are numerous algorithms for finding solutions to equations of this form. In this recipe, we will use the Newton-Raphson and secant methods to solve an equation of the form .

The Newton-Raphson method (Newton’s method) and the secant method are good, standard root-finding algorithms that can be applied in almost any situation. These are iterative methods that start with an approximation of the root and iteratively improve this approximation until it lies within a given tolerance.

To demonstrate these techniques, we will use the function from the Differentiating and integrating symbolically using SymPy recipe, defined by the following formula:

This is...

Integrating functions numerically using SciPy

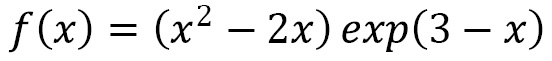
Integration can be interpreted as the area that lies between a curve and the axis, signed according to whether this area is above or below the axis. Some integrals cannot be computed directly using symbolic means, and instead, have to be approximated numerically. One classic example of this is the Gaussian error function, which was mentioned in the Understanding basic mathematical functions section in Chapter 1, An Introduction to Basic Packages, Functions, and Concepts. This is defined by the following formula:

Furthermore, the integral that appears here cannot be evaluated symbolically.

In this recipe, we will see how to use numerical integration routines in the SciPy package to compute the integral of a function.

Getting ready

We use the scipy.integrate module, which contains several routines for computing numerical integrals. We also import the NumPy library as np. We import this module as follows...

Solving simple differential equations numerically

Differential equations arise in situations where a quantity evolves, usually over time, according to a given relationship. They are extremely common in engineering and physics, and appear quite naturally. One of the classic examples of a (very simple) differential equation is the law of cooling devised by Newton. The temperature of a body cools at a rate proportional to the current temperature. Mathematically, this means that we can write the derivative of the temperature of the body at time using the following differential equation:

Here, is a positive constant that determines the rate of cooling. This differential equation can be solved analytically by first separating the variables and then integrating and rearranging them. After performing this procedure, we obtain the general solution:

Here, is the initial temperature.

In this recipe, we will solve a simple ODE numerically...

Solving systems of differential equations

Differential equations sometimes occur in systems consisting of two or more interlinked differential equations. A classic example is a simple model of the populations of competing species. This is a simple model of competing species labeled (the prey) and (the predators) given by the following equations:

The first equation dictates the growth of the prey species , which, without any predators, would be exponential growth. The second equation dictates the growth of the predator species , which, without any prey, would be exponential decay. Of course, these two equations are coupled; each population change depends on both populations. The predators consume the prey at a rate proportional to the product of their two populations, and the predators grow at a rate proportional to the relative abundance of prey (again the product of the two populations).

In this recipe, we will analyze a simple system of differential...

Solving partial differential equations numerically

Partial differential equations are differential equations that involve partial derivatives of functions in two or more variables, as opposed to ordinary derivatives in only a single variable. Partial differential equations are a vast topic, and could easily fill a series of books. A typical example of a partial differential equation is the (one-dimensional) heat equation:

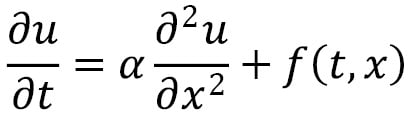
Here, is a positive constant and is a function. The solution to this partial differential equation is a function , which represents the temperature of a rod, occupying the range , at a given time . To keep things simple, we will take , which amounts to saying that no heating/cooling is applied to the system, , and . In practice, we can rescale the problem to fix the constant , so this is not a restrictive problem. In this example, we will use boundary conditions:

These are equivalent to saying that the ends...

Using discrete Fourier transforms for signal processing

One of the most useful tools coming from calculus is the Fourier transform (FT). Roughly speaking, the FT changes the representation, in a reversible way, of certain functions. This change of representation is particularly useful in dealing with signals represented as a function of time. In this instance, the FT takes the signal and represents it as a function of frequency; we might describe this as transforming from signal space to frequency space. This can be used to identify the frequencies present in a signal for identification and other processing. In practice, we will usually have a discrete sample of a signal, so we have to use the discrete Fourier transform (DFT) to perform this kind of analysis. Fortunately, there is a computationally efficient algorithm, called the FFT, for applying the DFT to a sample.

We will follow a common process for filtering a noisy signal using the FFT. The first step is to apply the FFT and...

Automatic differentiation and calculus using JAX

JAX is a linear algebra and automatic differentiation framework developed by Google for ML. It combines the capabilities of Autograd and its Accelerated Linear Algebra (XLA) optimizing compiler for linear algebra and ML. In particular, it allows us to easily construct complex functions, with automatic gradient computation, that can be run on Graphics Processing Units (GPUs) or Tensor Processing Units (TPUs). On top of all of this, it is relatively simple to use. In this recipe, we see how to make use of the JAX just-in-time (JIT) compiler, get the gradient of a function, and make use of different computation devices.

Getting ready

For this recipe, we need the JAX package installed. We will make use of the Matplotlib package, with the pyplot interface imported as plt as usual. Since we’re going to plot a function of two variables, we also need to import the mplot3d module from the mpl_toolkits package.

How to do it…...

Solving differential equations using JAX

JAX provides a set of tools for solving a wide array of problems. Solving differential equations—such as initial value problems described in the Solving simple differential equations numerically recipe—should be well within the capabilities of this library. The diffrax package provides various solvers for differential equations leveraging the power and convenience of JAX.

In the earlier recipe, we solved a relatively simple first-order ODE. In this recipe, we’re going to solve a second-order ODE to illustrate the technique. A second-order ODE is a differential equation that involves both the first and second derivatives of a function. To keep things simple, we’re going to solve a linear second-order ODE of the following form:

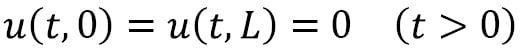
Here, is a function of to be found. In particular, we’re going to solve the following equation:

The initial conditions are and...

Further reading

Calculus is a very important part of every undergraduate mathematics course. There are a number of excellent textbooks on calculus, including the classic textbook by Spivak and the more comprehensive course by Adams and Essex:

• Spivak, M. (2006). Calculus. 3rd ed. Cambridge: Cambridge University Press.
• Adams, R. and Essex, C. (2018). Calculus: A Complete Course. 9th ed. Don Mills, Ont: Pearson.

A good source for numerical differentiation and integration is the classic Numerical Recipes book, which gives a comprehensive description of how to solve many computational problems in C++, including a summary of the theory:

• Press, W., Teukolsky, S., Vetterling, W. and Flannery, B. (2007). Numerical Recipes: The Art of Scientific Computing. 3rd ed. Cambridge: Cambridge University Press.