In this chapter, you will learn about a classic reinforcement learning experiment, which is also an established benchmark for testing various implementations of the control strategies. In this chapter, we consider three modifications of the cart-pole balancing experiment and develop control strategies that can be used to stabilize the cart-pole apparatuses of given configurations. You will learn how to write accurate simulations of real-life physical systems and how to use them for a definition of the objective function for the NEAT algorithm. After this chapter, you will be ready to apply the NEAT algorithm to implement controllers that can be directly used to control physical appliances.
In this chapter, we will cover the following topics:
- The single-pole balancing problem in reinforcement learning
- Implementation of the simulator of the cart-pole...























































 is the expected number of time steps from the configuration of the experiment, and
is the expected number of time steps from the configuration of the experiment, and  is the actual number of time steps during which the controller was able to maintain a stable pole balancer state within allowed bounds (refer to the reinforcement signal definition...
is the actual number of time steps during which the controller was able to maintain a stable pole balancer state within allowed bounds (refer to the reinforcement signal definition...
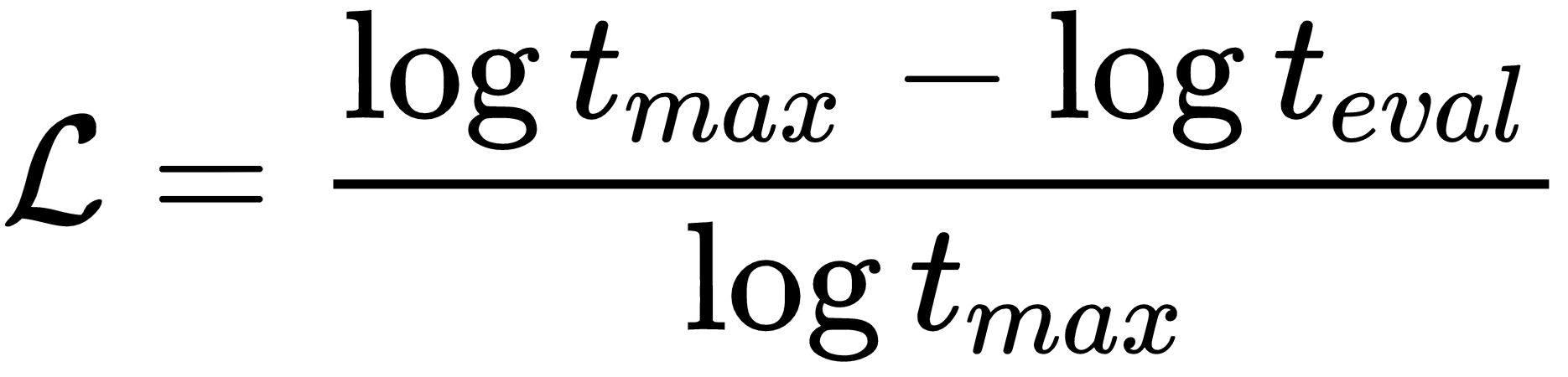
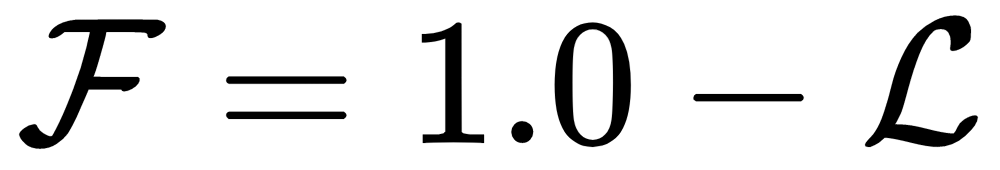
 is the expected number of time steps specified in the configuration of the experiment (100,000), and
is the expected number of time steps specified in the configuration of the experiment (100,000), and  is the actual number of time steps during which the controller was able to maintain
is the actual number of time steps during which the controller was able to maintain 











