7
A Primer on
Quaternions and Splines
Welcome to Chapter 7! In the previous chapter, we had a deeper view of the vector and matrix mathematical elements and data types. Both types are important building blocks of every 3D graphical application, as the internal storage and the calculation of virtual objects rely to a large extent on vertices and matrices.
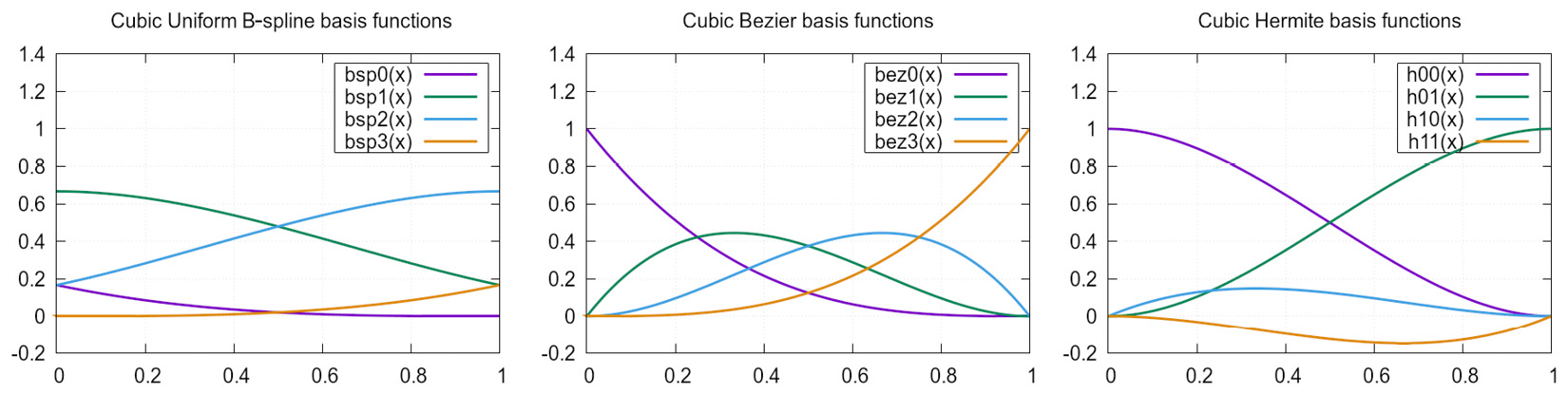
In this chapter, two other mathematical elements will be introduced: quaternions and splines, especially cubic Hermite splines. These two elements are heavily used in the glTF file format we use for the animated characters. The glTF file format will be explored in detail in Part 3 of the book, starting with Chapter 8.
By the end of the chapter, you should have a basic understanding of what quaternions and splines are, and how to work with them. You should also know about their advantages in character animations. Having a picture in your mind of the two elements and their transformations will help you master the rest of the...
























































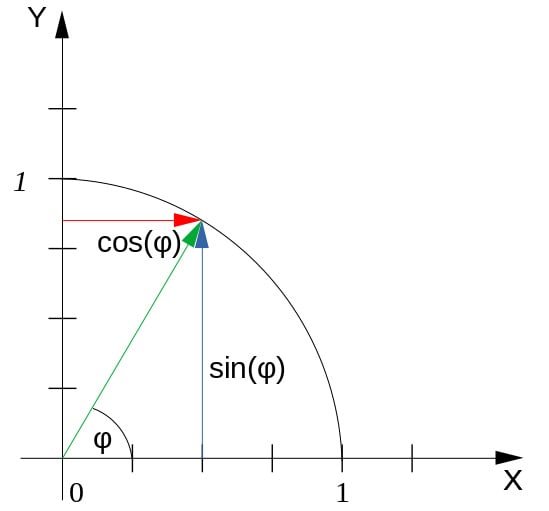



 and
and  has a second solution: the other way around the circle, starting on
has a second solution: the other way around the circle, starting on  and going “downward.” It is not guaranteed that Spherical Linear Interpolation will use the shortest path between two quaternions; this must be checked in the implementation...
and going “downward.” It is not guaranteed that Spherical Linear Interpolation will use the shortest path between two quaternions; this must be checked in the implementation...