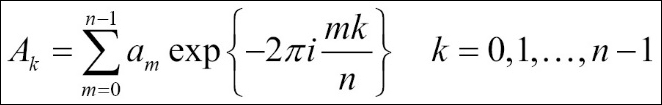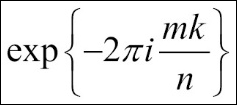Chapter 6. Fourier Analysis in NumPy

Fourier analysis is commonly used, among other things, for digital signal processing. This is thanks to it being so powerful in separating its input signals (time domain) into components that contribute at discrete frequencies (frequency domain). Another fast algorithm to compute Discrete Fourier transform (DFT) was developed, which is well known as Fast Fourier transform (FFT), and it provides more possibilities for analysis and its applications. NumPy, as it targets numeric computing, also supports FFT. Let's try to use NumPy to apply some Fourier analysis on applications! Note, no familiarity with signal processing or Fourier methods is assumed in this chapter.

The topics that will be covered in this chapter are:

• The basics of Fourier analysis
• One and two-dimensional Fourier transformations
• Spectral density estimation
• Time frequency analysis

Before we start

As we all know, Fourier analysis expresses a function as a sum of periodic components (a combination of sine and cosine functions) and these components are able to recover the original function. It has great applications in digital signal processing such as filtering, interpolation, and more, so we don't want to talk about Fourier analysis in NumPy without giving details of any application we can use it for. For this, we need a module to visualize it.

Matplotlib is the module we are going to use in this chapter for visualization. Please download and install it from the official website: http://matplotlib.org/downloads.html. Or if you are using Scientific Python distributions such as Anaconda, then matplotlib should already be included.

We are going to write a simple display function called show() to help us with the practice examples in this chapter. The function output will be as shown in the following graph:

The upper plot area shows the original functions (signal), and...

Signal processing

In this section, we are going to use NumPy functions to simulate several signal functions and translate them to Fourier transforms. We will focus on using numpy.fft and its related functions. We hope after this section that you will get some sense of using a Fourier transformation in NumPy. The theory part will be covered in the next section.

The first example we are going to use is our heartbeat signal, which is a series of sine waves. The frequency is 60 beats per minutes (1 Hz), and our sampling period is 5 seconds long, with a sampling interval of 0.005 seconds. Let's create the sine wave first:

In [1]: time = np.arange(0, 5, .005) 
In [2]: x = np.sin(2 * np.pi * 1 * time) 
In [3]: y = np.fft.fft(x) 
In [4]: show(x, y) 

In this example, we first created the sampling time interval and saved it to anndarray called time. And we passed the time array times 2π and its frequency 1 Hz to the numpy.sin() method to create the sine wave (x). Then applied the...

Fourier analysis

There are many ways to define the DFT; however, in a NumPy implementation, the DFT is defined as the following equation:

A _k represents the discrete Fourier transform and a_m represents the original function. The transformation from a_m->A_k is a translation from the configuration space to the frequency space. Let's calculate this equation manually to get a better understanding of the transformation process. We will use a random signal with 500 values:

In [25]: x = np.random.random(500) 
In [26]: n = len(x) 
In [27]: m = np.arange(n) 
In [28]: k = m.reshape((n, 1)) 
In [29]: M = np.exp(-2j * np.pi * k * m / n) 
In [30]: y = np.dot(M, x) 

In this code block, x is our simulated random signal, which contain 500 values and corresponds to a_m in the equation. Based on the size of x, we calculate the sum product of:

We then save it to M. The final step is to use the matrix multiplication between M and x to generate DFT and save it to y.

Let's...

Fourier transform application

In the previous sections, you learned how to use numpy.fft for a one and multi-dimensional ndarray, and saw the implementation details underneath the hood. Now it's time for some applications. In this section, we are going to use the Fourier transform to do some image processing. We will analyze the spectrum, and then we will interpolate the image to enlarge it to twice the size. First, let's download the exercise image from the Packt Publishing website blog post:  https://www.packtpub.com/books/content/python-data-scientists. Save the image to your local directory as scientist.png.

This is a RGB image, which means that, when we convert it to an ndarray, it will be three-dimensional. To simplify the exercise, we use the image module in matplotlib to read in the image and convert it to grayscale:

In [52]: from matplotlib import image 
In [53]: img = image.imread('./scientist.png') 
In [54]: gray_img = np.dot(img[:,:,:3], [.21, .72, .07]) 
In [55...

Summary

In this chapter, we covered the usage of one and multi-dimensional Fourier transformations and how they are applied in signal processing. You now understand the implementation of the discrete Fourier transform in NumPy, and we did a performance comparison between our manual implemented script with NumPy built-in modules.

We also accomplished a real-world application of image interpolation, and we got a plus one for knowing some basics of the matplotlib packages.

In the next chapter, we will see how to distribute our code using the numpy.distutils() submodules.