Overview

In this chapter, we will take a look at geometric transformations – rotation, translation, scaling, affine transformation, and perspective transformation. We will crop images using NumPy and OpenCV functions. Then, we will discuss binary images and how to carry out arithmetic operations on images. We will have a look at some real-life applications where these techniques can come in handy.

By the end of this chapter, you should have a fairly good idea of how to process images for your specific case study. You will be able to use affine transformations on images and carry out tasks such as motion identification using binary operations.

If you've ever seen a "behind-the-scenes" video of your favorite Hollywood movie, you might have noticed that some of the animated scenes are shot in front of a green screen. Then, during editing, the green screen is replaced with a mind-blowing futuristic vista or a dystopian scene that's beyond your wildest imagination.

Now, think of one single frame from that scene in the movie. The original frame was shot in front of a green background. Then, the image was modified to obtain a particular result, that is, a different background.

Furthermore, sometimes, you want to process an image to directly obtain the result you seek so that you can receive an intermediate result that will make further steps easier and achievable. The following is a sample picture that was taken in front of the green screen:

Figure 2.1: A picture taken in front of a green screen

This activity of modifying or processing an image to obtain a particular result is known as image processing.

In the previous chapter, we went over the basics of images – what pixels are, what pixel coordinates are, how to extract pixel values using pixel coordinates, and more. We'll start this chapter by understanding what we mean by image processing and why we need it. By the end of this chapter, you will be able to process images such as the one shown previously and replace the green screen with a background of your choice using a very basic image processing technique referred to as masking.

This chapter can be broken down into two major parts. First, we will focus on basic techniques, such as translation, rotation, resizing, and cropping, and a more general geometric transformation called affine transformation. We will end the section by looking at perspective transformation. Then, we will discuss binary images and arithmetic operations that we can carry out on images. We will also talk about masking in this section.

Both sections will be accompanied by exercises and activities that you can try to complete. Now, let's start with the first section of this chapter – Geometric Transformations.

Often, during image processing, the geometry of the image (such as the width and height of the image) needs to be transformed. This process is called geometric transformation. As we saw in the Images in OpenCV section of Chapter 1, Basics of Image Processing, images are nothing but matrices, so we can use a more mathematical approach to understand these topics.

Since images are matrices, if we apply an operation to the images (matrices) and we end up with another matrix, we call this a transformation. This basic idea will be used extensively to understand and apply various kinds of geometric transformations.

Here are the geometric transformations that we are going to discuss in this chapter:

• Translation
• Rotation
• Image scaling or resizing
• Affine transformation
• Perspective transformation

While discussing image scaling, we will also discuss image cropping. which isn't actually a geometric transformation, though it is commonly used along with resizing.

First, we will go over image translation, where we will discuss moving an image in a specified direction.

Image Translation

Image translation is also referred to as shifting an image. In this transformation, our basic intention is to move an image along a line. Take a look at the following figure:

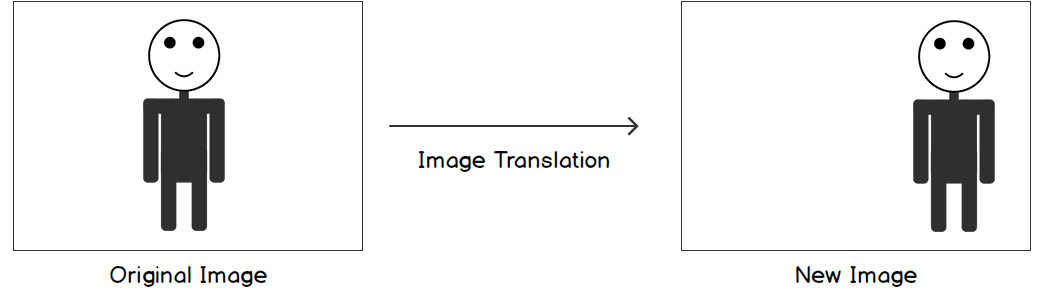
Figure 2.2: Image translation

For example, if we consider the following figure, we are shifting the human sketch to the right. We can shift an image in both the X and Y directions, as well as separately. What we are doing in this process is shifting every pixel's location in the image in a certain direction. Consider the following figure:

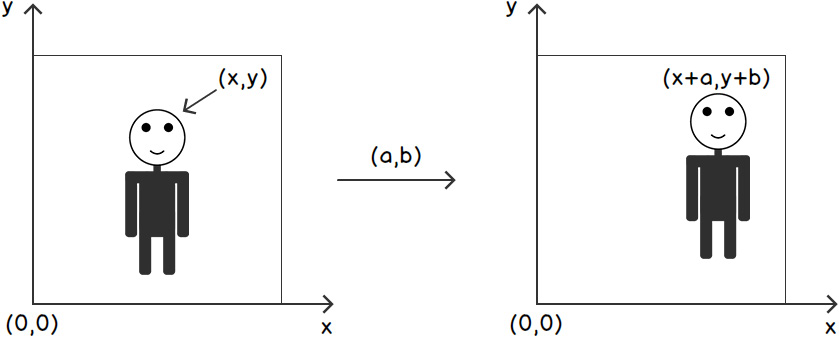
Figure 2.3: Pixel view of image translation

Using the preceding figure as reference, we can represent image translation with the following matrix equation:

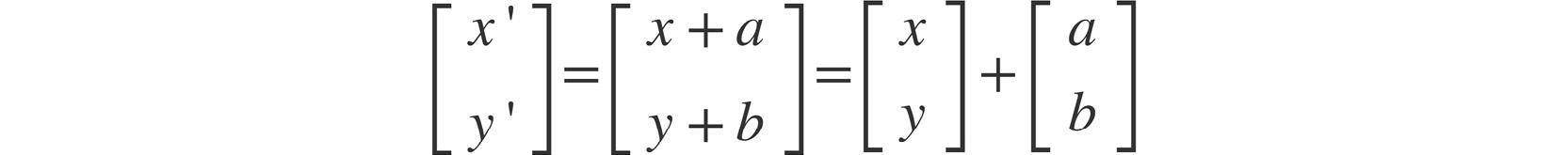
Figure 2.4: Representation of an image matrix

In the preceding equation, x' and y' represent the new coordinates of a point/pixel after it has been shifted by a units in the x direction and b units in the y direction.

Note

Even though we have discussed image translation, it is very rarely used in image processing. It is usually combined with other transformations to create a more complex transformation. We will be studying this general class of transformations in the Affine Transformations section.

Now that we have discussed the theory of image translation, let's understand how translation can be performed using NumPy. We stated that images are nothing but NumPy arrays while using them in OpenCV in Python. Similarly, geometric transformations are just matrix multiplications. We also saw how image translation can be represented using a matrix equation. In terms of matrix multiplication, the same image equation can be written as a NumPy array:

M = np.array([[1,0,a],[0,1,b],[0,0,1])

If you look carefully, you will notice that the first two columns of this matrix form an identity matrix ([[1,0],[0,1]]). This signifies that even though we are transforming the image, the image dimensions (width and height) will stay the same. The last column is made up of a and b, which signifies that the image has been shifted by a units in the x direction and b units in the y direction. The last row, - [0,0,1], is only used to make the matrix, M, a square matrix – a matrix with the same number of rows and columns. Now that we have the matrix for image translation with us, whenever we want to shift an image, all we need to do is multiply the image, let's say, img (as a NumPy array), with the array, M. This can be performed as follows:

output = M@img

Here, output is the output that's obtained after image translation.

Note that in the preceding code, it's assumed that every point that we want to shift represents a column in the matrix, that is, img. Moreover, usually, an extra row full of ones is also added in the img matrix. That's simply to make sure that that matrix multiplication can be carried out. To understand it, let's understand the dimensions of the matrix, M. It has three rows and three columns. For the matrix multiplication of M and img to be carried out, img should have the same number of rows as the number of columns in matrix M, that is, three.

Now, we also know that a point is represented as a column in the img matrix. We already have the x coordinate of the point in the first row and the y coordinate of the point in the second row of the img matrix. To make sure that we have three rows in the img matrix, we add 1 in the third row.

For example, point [2,3] will be presented as [[2],[3],[1]], that is, 2 is present in the first row, 3 is present in the second row. and 1 is present in the third row.

Similarly, if we want to represent two points – [2,3] and [1,0] – they will be represented as [[2,1],[3,0],[1,1]]; that is, the x coordinates of both points (2 and 1) are present in the first row, the y coordinates (3 and 0) are present in the second row, and the third row is made up of 1s.

Let's understand this better with the help of an exercise.

Exercise 2.01: Translation Using NumPy

In this exercise, we will carry out the geometric transformation known as translation using NumPy. We will be using the translation matrix that we looked at earlier to carry out the translation. We will be shifting 3 points by 2 units in the x direction and 3 units in the y direction. Let's get started:

1. Create a new Jupyter Notebook – Exercise2.01.ipynb. We will be writing our code in this notebook.
2. First, let's import the NumPy module:

   # Import modules
   import numpy as np

3. Next, we will specify the three points that we want to shift – [2,3], [0,0], and [1,2]. Just as we saw previously, the points will be represented as follows:

   # Specify the 3 points that we want to translate
   points = np.array([[2,0,1],
                     [3,0,2],
                     [1,1,1]])

   Note how the x coordinates (2, 0, and 1) make up the first row, the y coordinates (3, 0, and 2) make up the second row, and the third row has only 1s.

4. Let's print the points matrix:

   print(points)

   The output is as follows:

   [[2 0 1]
    [3 0 2]
    [1 1 1]]

5. Next, let's manually calculate the coordinates of these points after translation:

   # Output points - using manual calculation
   outPoints = np.array([[2 + 2, 0 + 2, 1 + 2],
               [3 + 3, 0 + 3, 2 + 3],
               [1, 1, 1]])

6. Let's also print the outPoints matrix:

   print(outPoints)

   The output is as follows:

   [[4 2 3]
    [6 3 5]
    [1 1 1]]

7. We need to shift these points by 2 units in the x direction and 3 units in the y direction:

   # Move by 2 units along x direction
   a = 2
   # Move by 3 units along y direction
   b = 3

8. Next, we will specify the translation matrix, as we saw previously:

   # Translation matrix
   M = np.array([[1,0,a],[0,1,b],[0,0,1]])

9. Now, we can print the translation matrix:

   print(M)

   The output is as follows:

   [[1 0 2]
    [0 1 3]
    [0 0 1]]

10. Now, we can perform the translation using matrix multiplication:

    # Perform translation using NumPy
    output = M@points

11. Finally, we can display the output points by printing them:

    print(output)

    The output is as follows:

    [[4 2 3]
     [6 3 5]
     [1 1 1]]

Notice how the output points obtained using NumPy and using manual calculation match perfectly. In this exercise, we shifted the given points using manual calculation, as well as using matrix multiplication. We also saw how we can carry out matrix multiplication using the NumPy module in Python. The key point to focus on here is that transition is nothing but a matrix operation, just as we discussed previously at the beginning of the Geometric Transformations section.

Note

To access the source code for this specific section, please refer to https://packt.live/3eQdjhR.

So far, we've discussed moving an image along a direction. Next, let's discuss rotating an image around a specified point at a given angle.

Image Rotation

Image rotation, as the name suggests, involves rotating an image around a point at a specified angle. The most common notation is to specify the angle as positive if it's anti-clockwise and negative if it's specified in the clockwise direction. We will assume angles in a non-clockwise direction are positive. Let's see whether we can derive the matrix equation for this. Let's consider the case shown in the following diagram: w and h refer to the height and width of an image, respectively. The image is rotated about the origin (0,0) at an angle, alpha (α), in an anti-clockwise direction:

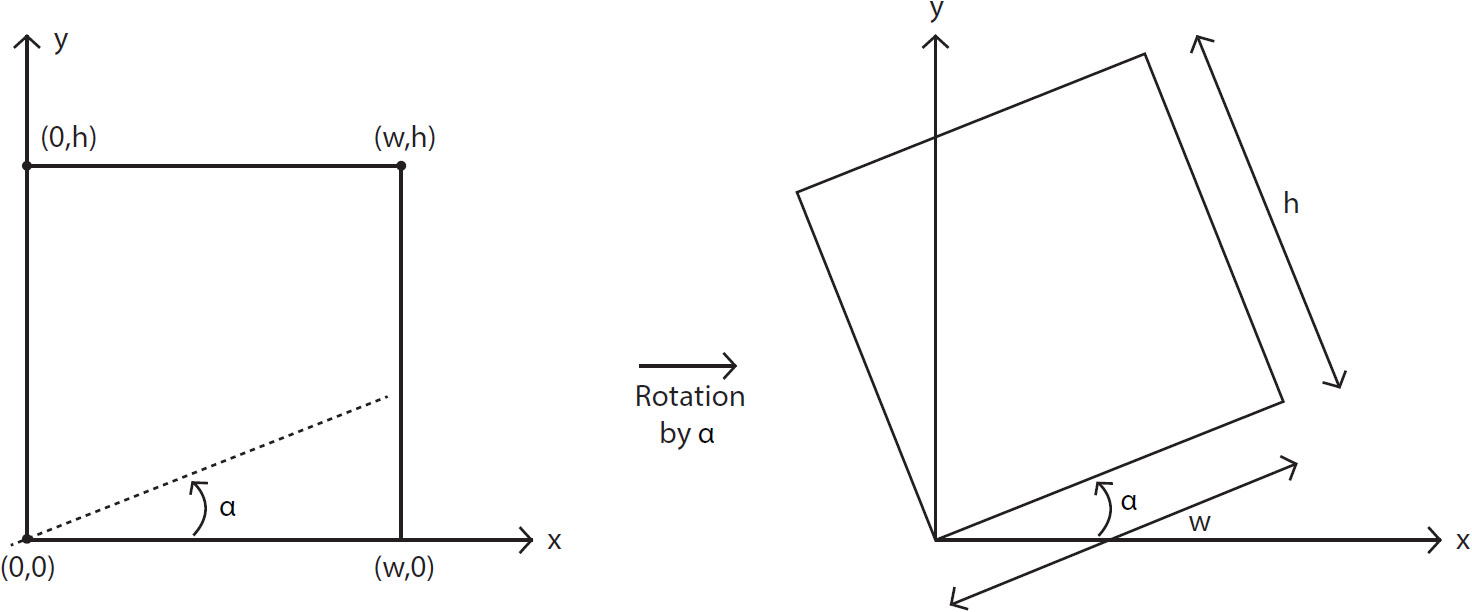
Figure 2.5: Image rotation

One thing that we can note very clearly here is that the distance between a point and the origin stays the same, even after rotation. We will be using this point when deriving the rotation matrix.

We can divide the entire problem into two parts:

• Finding the rotation matrix
• Finding the size of the new image

Finding the Rotation Matrix

Let's consider a point, P(x,y), which, after rotation by angle β around the origin, O(0,0), is transformed into P'(x',y'). Let's also assume the distance between point P and origin O is r:

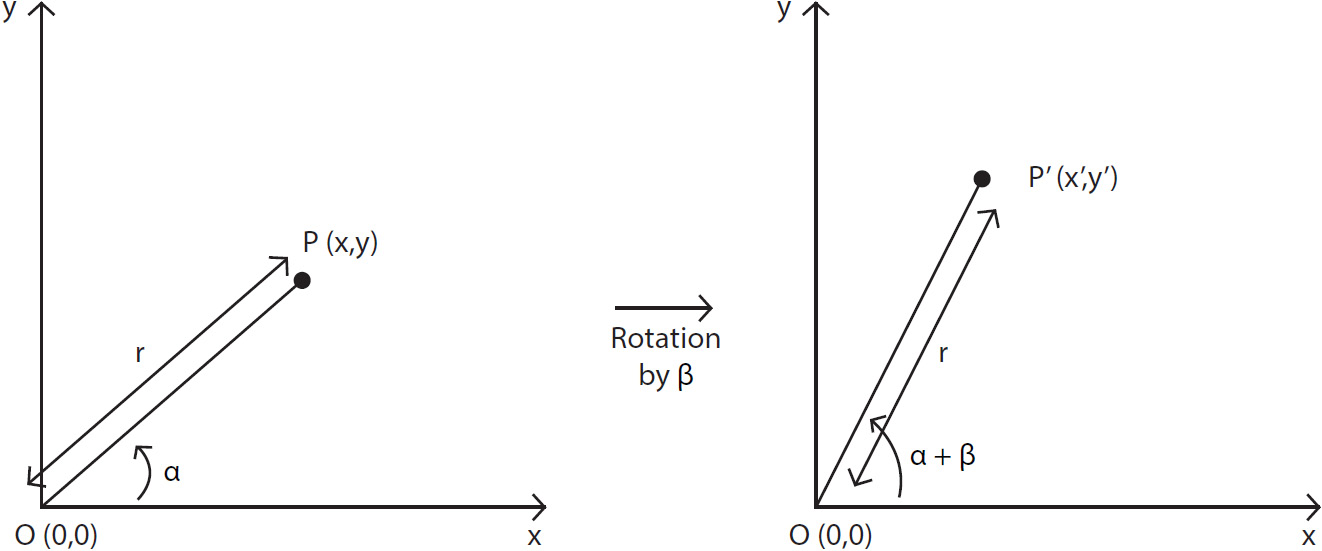
Figure 2.6: Point rotation

In the following equation, we have used the distance formula to obtain the distance between P and O:

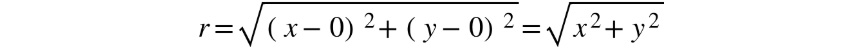
Figure 2.7: Distance formula

Since we know that this distance will stay the same, even after rotation, we can write the following equation:

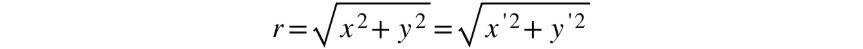
Figure 2.8: Distance formula after rotation

Let's assume that the P(x,y) point makes an angle, α, with the X-axis. Here, the formula will look as follows:

x = r cos(α)
y = r sin(α)

Similarly, the P'(x',y') point will make an angle, α + β, with the X-axis. Thus, the formula will look as follows:

x' = r cos(α + β)
y› = r sin(α + β)

Next, we will use the following trigonometric identity:

cos(α + β) = cos α cos β – sin α sin β

Thus, we can now simplify the equation for x', as follows:

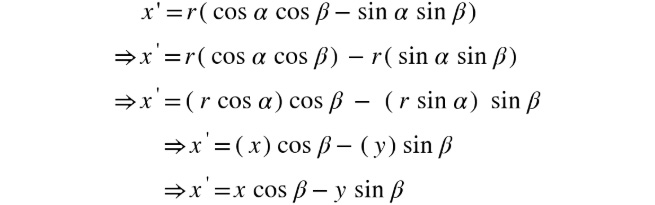
Figure 2.9: Simplified equation for x'

Similarly, let's simplify the equation for y' using the following trigonometric identity:

sin(α + β) = sin α cos β – cos α sin β

Using the preceding equation, we can simplify y' as follows:

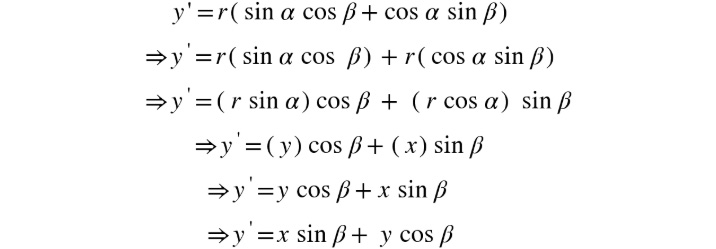
Figure 2.10: Simplified equation for y'

We can now represent x' and y' using the following matrix equation:

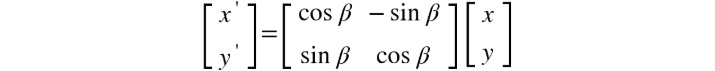
Figure 2.11: Representing x' and y' using the matrix equation

Now that we have obtained the preceding equation, we can transform any point into a new point if it's rotated by a given angle. The same equation can be applied to every pixel in an image to obtain the rotated image.

But have you ever seen a rotated image? Even though it's rotated, it still lies within a rectangle. This means the dimensions of the new image can change, unlike in translation, where the dimensions of the output image and the input image stayed the same. Let's see how we can find the dimensions of the image.

Finding the Size of the Output Image

We will consider two cases here. The first case is that we keep the dimensions of the output image the same as the ones for the input image, while the second case is that we modify the dimensions of the output image. Let's understand the difference between them by looking at the following diagram. The left half shows the case when the image dimensions are kept the same, even after rotation, whereas in the right half of the diagram, we relax the dimensions to cover the entire rotated image. You can see the difference in the results obtained in both cases. In the following diagram, L and H refer to the dimensions of the original image, while L' and H' refer to the dimensions after rotation.

The image is rotated by an angle, ϴ, in an anti-clockwise direction, around the center of the image:

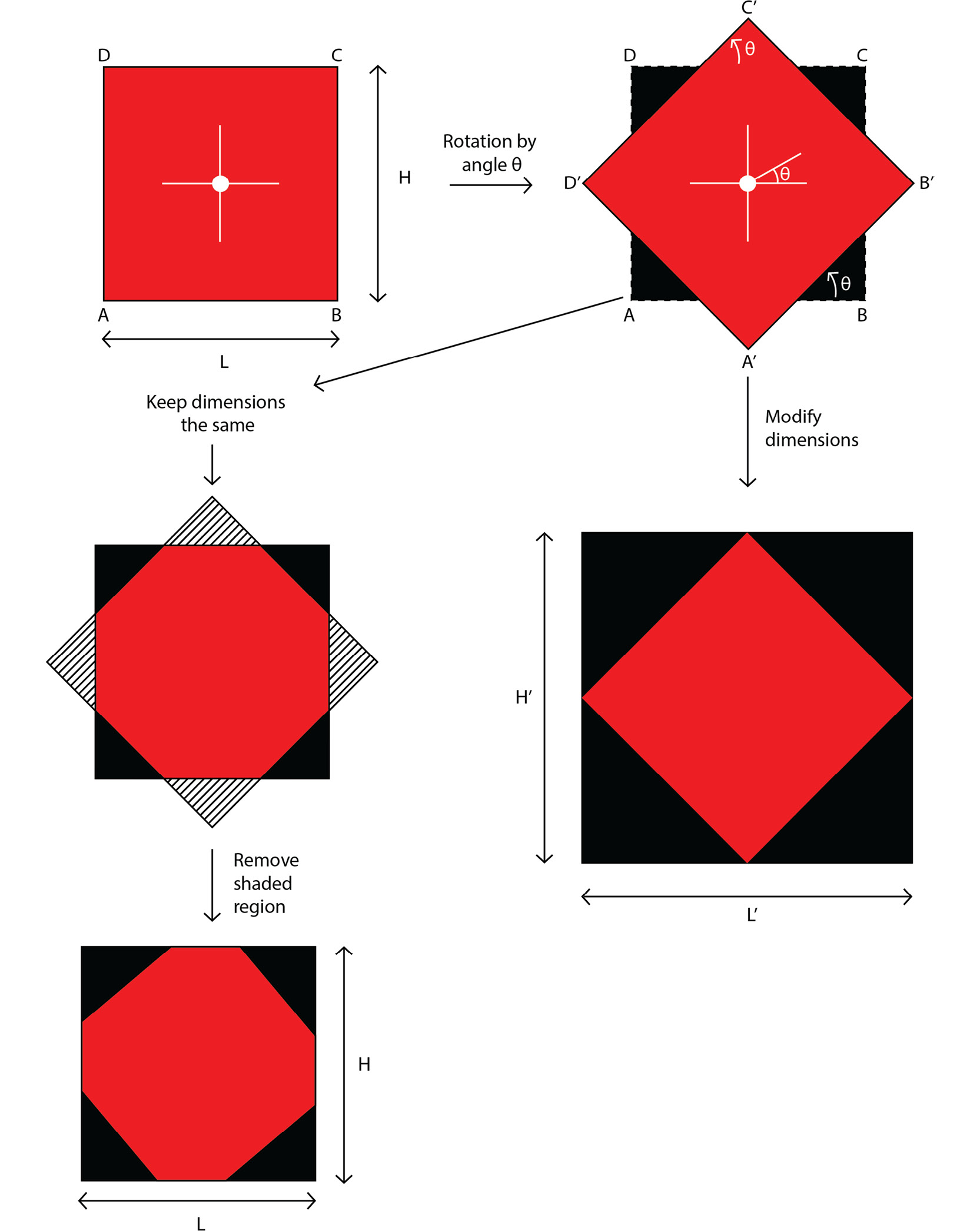
Figure 2.12: Size of the rotated image

In Figure 2.12, the size of the rotated image is presented depending on whether the image dimensions are kept the same or are modified while rotating the image

For the case where we want to keep the size of the image the same as the initial image's size, we just crop out the extra region. Let's learn how to obtain the size of the rotated image, if we don't want to keep the dimensions the same:

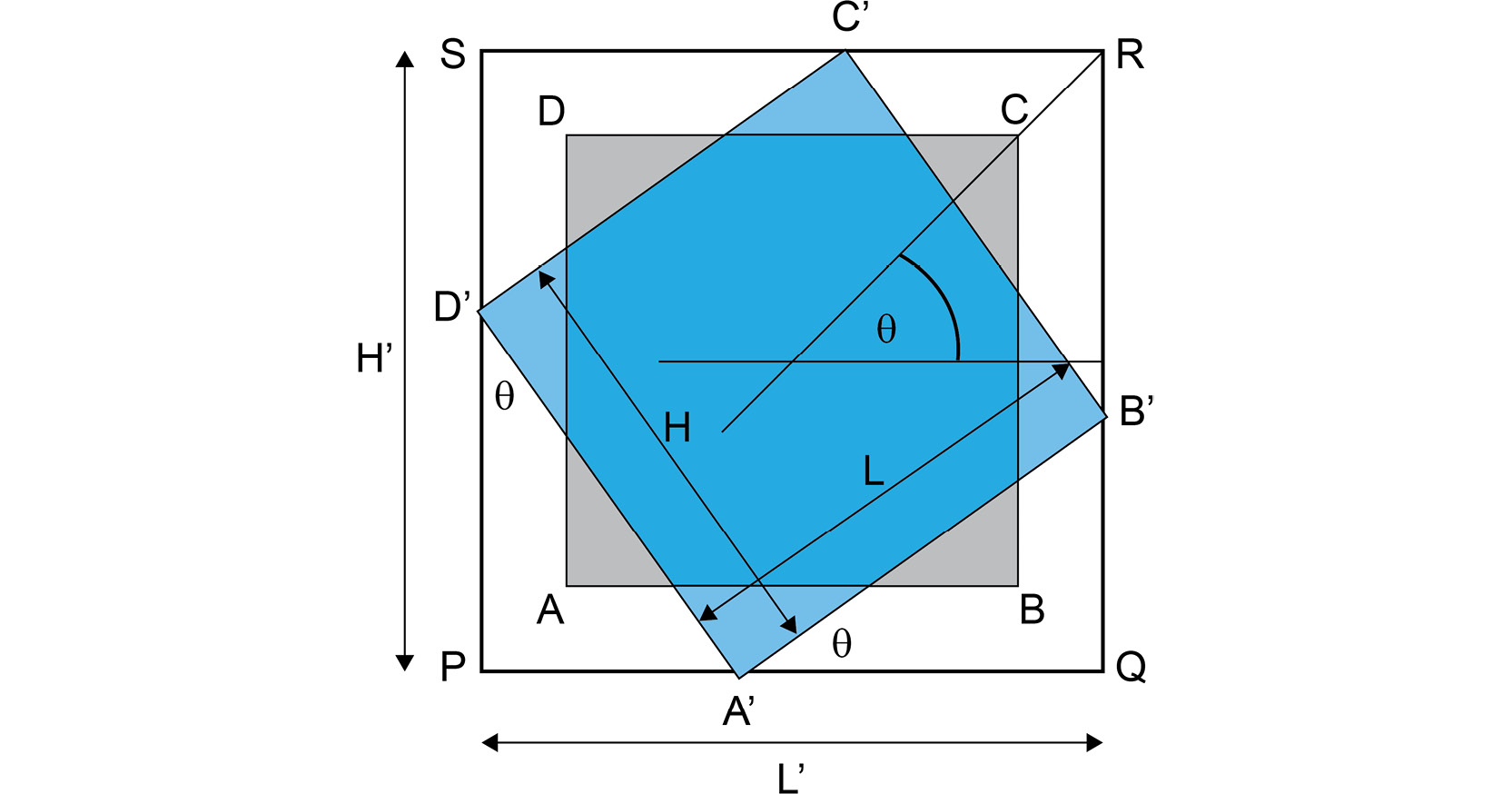
Figure 2.13: Size of the image after rotation

In the preceding diagram, the original image, ABCD, has been rotated along the center of the image by an angle, θ, to form the new image A'B'C'D'.

Referring to the preceding diagram, we can write the following equations:

A'Q = L cos θ
A›P = H sin θ

Thus, we can obtain L' in terms of L and H as follows. Note that L' refers to the size of the image after rotation. Refer to the preceding diagram for a visual representation:

L' = PQ = PA' + A'Q = H sin θ + L cos θ

Similarly, we can write the following equations:

PD' = H cos θ
D›S = L sin θ

Thus, we can obtain H' in terms of L and H, as follows:

H' = PS = PD' + D'S = L sin θ + H cos θ

Here comes a tricky part. We know the values of cosine and sine can also be negative, but the size of the rotated image cannot be smaller than the size of the input image. Thus, we will use the absolute values of sine and cosine. The equations for L' and H' will be modified so that they look as follows:

L' = L|cos θ| + H | sin θ|
H› = L|sin θ| + H | cos θ|

We can round off these values to obtain an integer value for the new width and height of the rotated image.

Now comes the question that you might be wanting to ask by now. Do we have to do all this calculation every time we want to rotate an image? Luckily, the answer is no. OpenCV has a function that we can use if we want to rotate an image by a given angle. It also gives you the option of scaling the image. The function we are talking about here is the cv2.getRotationMatrix2D function. It generates the rotation matrix that can be used to rotate the image. This function takes three arguments:

• The point that we want to rotate the image around. Usually, the center of the image or the bottom-left corner is chosen as the point.
• The angle in degrees that we want to rotate the image by.
• The factor that we want to change the dimensions of the image by. This is an optional argument and can be used to shrink or enlarge the image. In the preceding case, it was 1 as we didn't resize the image.

Note that we are only generating the rotation matrix here and not actually carrying out the rotation. We will cover how to use this matrix when we will look at affine transformations. For now, let's have a look at image resizing.

Image Resizing

Imagine that you are training a deep learning model or using it to carry out some prediction – for example, object detection, image classification, and so on. Most deep learning models (that are used for images) require the input image to be of a fixed size. In such situations, we resize the image to match those dimensions. Image resizing is a very simple concept where we modify an image's dimensions. This concept has its applications in almost every computer vision domain (image classification, face detection, face recognition, and so on).

Images can be resized in two ways:

• Let's say that we have the initial dimensions as W×H, where W and H stand for width and height, respectively. If we want to double the size (dimensions) of the image, we can resize or scale the image up to 2W×2H. Similarly, if we want to reduce the size (dimensions) of the image by half, then we can resize or scale the image down to W/2×H/2. Since we just want to scale the image, we can pass the scaling factors (for length and width) while resizing. The output dimensions can be calculated based on these scaling factors.
• We might want to resize an image to a fixed dimension, let's say, 420×360 pixels. In such a situation, scaling won't work as you can't be sure that the initial dimensions are going to be a multiple (or factor) of the fixed dimension. This requires us to pass the new dimensions of the image directly while resizing.

A very interesting thing happens when we resize an image. Let's try to understand this with the help of an example:

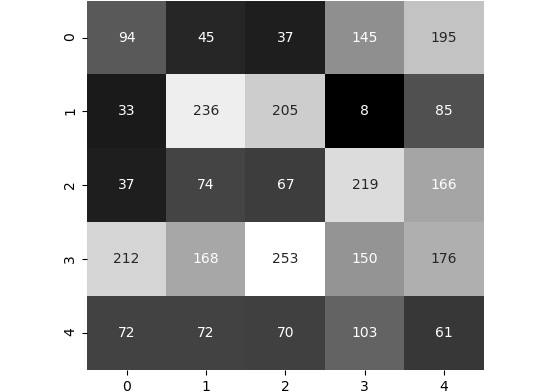
Figure 2.14: Image to resize

The preceding figure shows the image and the pixel values that we want to resize. Currently, it's of size 5×5. Let's say we want to double the size. This results in the following output. However, we want to fill in the pixel values:

Figure 2.15: Resized image

Let's look at the various options we have. We can always replicate the pixels. This will give us the result shown in the following figure:

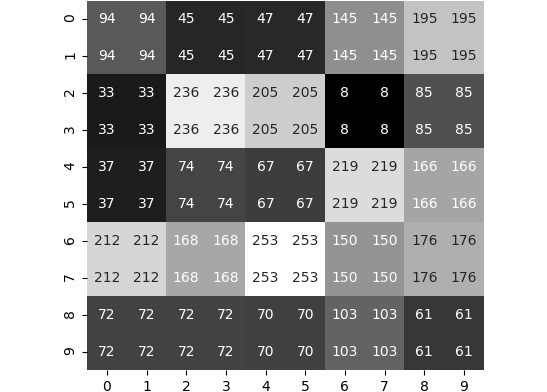
Figure 2.16: Resized image by replicating pixel values

If we remove the pixel values from the preceding image, we will obtain the image shown in the following figure. Compare this with the original image, Figure 2.14. Notice how similar it looks to the original image:

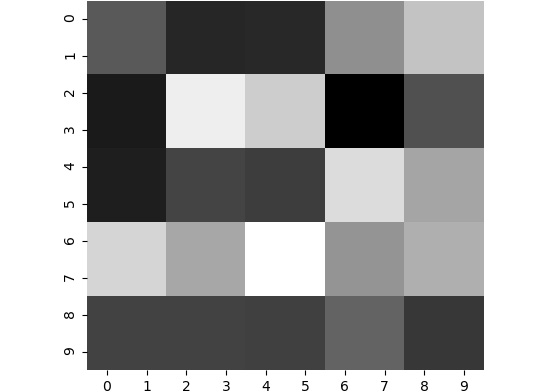
Figure 2.17: Resized image without annotation

Similarly, if we want to reduce the size of the image by half, we can drop some pixels. One thing that you would have noticed is that while resizing, we are replicating the pixels, as shown in Figure 2.16 and Figure 2.17. There are some other techniques we can use as well. We can use interpolation, in which we find out the new pixel values based on the pixel values of the neighboring pixels, instead of directly replicating them. This gives a nice smooth transition in colors. The following figure shows how the results vary if we use different interpolations. From the following figure, we can see that as we progress from left to right, the pixel values of the newly created pixels are calculated differently. In the first three images, the pixels are directly copied from the neighboring pixels, whereas in the later images, the pixel values depend on all the neighboring pixels (left, right, up, and down) and, in some cases, the diagonally adjacent pixels as well:

Figure 2.18: Different results obtained based on different interpolations used

Now, you don't need to worry about all the interpolations that are available. We will stick to the following three interpolations for resizing:

• If we are shrinking an image, we will use bilinear interpolation. This is represented as cv2.INTER_AREA in OpenCV.
• If we are increasing the size of an image, we will use either linear interpolation (cv2.INTER_LINEAR) or cubic interpolation (cv2.INTER_CUBIC).

Let's look at how we can resize an image using OpenCV's cv2.resize function:

cv2.resize(src, dsize, fx, fy, interpolation)

Let's have a look at the arguments of this function:

• src: This argument is the image we want to resize.
• dsize: This argument is the size of the output image (width, height). This will be used when you know the size of the output image. If we are just scaling the image, we will set this to None.
• fx and fy: These arguments are the scaling factors. These will only be used when we want to scale the image. If we already know the size of the output image, we will skip these arguments. These arguments are specified as fx = 5, fy = 3, if we want to scale the image by five in the x direction and three in the y direction.
• interpolation: This argument is the interpolation that we want to use. This is specified as interpolation = cv2.INTER_LINEAR if we want to use linear interpolation. The other interpolation flags have already been mentioned previously – cv2.INTER_AREA and cv2.INTER_CUBIC.

Next, let's have a look at a more general transformation – affine transformation.

Affine Transformation

Affine transformation is one of the most important geometric transformations in computer vision. The reason for this is that an affine transformation can combine the effects of translation, rotation, and resizing into one transform. Affine transformation in OpenCV uses a 2×3 matrix and then applies the effect using the matrix using the cv2.warpAffine function. This function takes three arguments:

cv2.warpAffine(src, M, dsize)

Let's take a look at each argument:

• The first argument (src) is the image that we want to apply the transformation to.
• The second argument (M) is the transformation matrix.
• The third argument (dsize) is the shape of the output image. The order that's used is (width, height) or (number of columns, number of rows).

Let's have a look at the transformation matrices for different transformations and how to generate them:

Figure 2.19: Table with transformation matrices for different transformations

To generate the transformation matrix for affine transformation, we choose any three non-collinear points on the input image and the corresponding points on the output image. Let's call the points (in1x, in1y), (in2x, in2y), (in3x, in3y) for the input image, and (out1x, out1y), (out2x, out2y), (out3x, out3y) for the output image.

Then, we can use the following code to generate the transformation matrix. We can use the following code to create a NumPy array for storing the points:

ptsInput = np.float32([[in1x, in1y],[in2x, in2y],\
                      [in3x, in3y]])

Alternatively, we can also use the following code:

ptsOutput = np.float32([[out1x, out1y], [out2x, out2y], \
                       [out3x, out3y]])

Next, we will pass these two NumPy arrays to the cv2.getAffineTransform function, as follows:

M = cv2.getAffineTransform(ptsInput, ptsOutput)

Now that we have seen how to generate the transformation matrix, let's see how to apply it. This can be done using outputImage = cv2.warpAffine(inputImage, M, (outputImageWidth, outputImageHeight)).

Now that we have discussed affine transformation and how to apply it, let's put this knowledge to use in the following exercise.

Exercise 2.02: Working with Affine Transformation

In this exercise, we will use the OpenCV functions that we discussed in the previous sections to translate, rotate, and resize an image. We will be using the following image in this exercise.

Figure 2.20: Image of a drop

Note

This image is available at https://packt.live/3geu9Hh.

Follow these steps to complete this exercise:

1. Create a new Jupyter Notebook – Exercise2.02.ipynb. We will be writing our code in this notebook.
2. Start by importing the required modules:

   # Import modules
   import cv2
   import numpy as np
   import matplotlib.pyplot as plt
   %matplotlib inline

3. Next, read the image.

   Note

   Before proceeding, be sure to change the path to the image (highlighted) based on where the image is saved in your system.

   The code is as follows:

   img = cv2.imread("../data/drip.jpg")

4. Display the image using Matplotlib:

   plt.imshow(img[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.21: Image with X and Y axes

5. Convert the image into grayscale for ease of use:

   img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

6. Store the height and width of the image:

   height,width = img.shape

7. Start with translation. Shift the image by 100 pixels to the right and 100 pixels down:

   # Translation
   tx = 100
   ty = 100
   M = np.float32([[1,0,tx],[0,1,ty]])
   dst = cv2.warpAffine(img,M,(width,height))
   plt.imshow(dst,cmap="gray")
   plt.show()

   The preceding code produces the following output. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.22: Translated image

8. Next, rotate our image 45 degrees anti-clockwise, around the center of the image, and scale it up twice:

   # Rotation
   angle = 45
   center = (width//2, height//2)
   scale = 2
   M = cv2.getRotationMatrix2D(center,angle,scale)
   dst = cv2.warpAffine(img,M,(width,height))
   plt.imshow(dst,cmap="gray")
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.23: Rotated image

9. Finally, double the size of the image using the cv2.resize function:

   # Resizing image
   print("Width of image = {}, Height of image = {}"\
         .format(width, height))
   dst = cv2.resize(img, None, fx=2, fy=2, \
                    interpolation=cv2.INTER_LINEAR)
   height, width = dst.shape
   print("Width of image = {}, Height of image = {}"\
         .format(width, height))

   The output is as follows:

   Width of image = 1280, Height of image = 849
   Width of image = 2560, Height of image = 1698

In this exercise, we learned how to translate, rotate, and resize an image using OpenCV functions.

Note

To access the source code for this specific section, please refer to https://packt.live/38iUnFZ.

Next, let's have a look at the final geometric transformation of this chapter – perspective transformation.

Perspective Transformation

Perspective transformation, unlike all the transformations we have seen so far, requires a 3×3 transformation matrix. We won't go into the mathematics behind this matrix as it's out of the scope of this book. We will need four points in the input image and the coordinates of the same points in the output image. Note that these points should not be collinear. Next, similar to the affine transformation steps, we will carry out perspective transformation.

We will use the following code create a NumPy array for storing the points:

ptsInput = np.float32([[in1x, in1y],[in2x, in2y],[in3x, in3y],\
                      [in4x,in4y]]) 

Alternatively, we can use the following code:

ptsOutput = np.float32([[out1x, out1y], [out2x, out2y], \
                       [out3x, out3y], [out4x, out4y]])

Next, we will pass these two NumPy arrays to the cv2.getPerspectiveTransform function:

M = cv2.getPerspectiveTransform(ptsInput, ptsOutput)

The transformation matrix can then be applied using the following code:

outputImage = cv2.warpPerspective(inputImage, M, \
              (outputImageWidth, outputImageHeight))

The primary difference between perspective and affine transformation is that in perspective transformation, straight lines will still remain straight after the transformation, unlike in affine transformation, where, because of multiple transformations, the line can be converted into a curve.

Let's see how we can use perspective transformation with the help of an exercise.

Exercise 2.03: Perspective Transformation

In this exercise, we will carry out perspective transformation to obtain the front cover of the book given as the input image. We will use OpenCV's cv2.getPerspectiveTransform and cv2.warpPerspective functions. We will be using the following image of a book:

Figure 2.24: Image of a book

Note

This image can be downloaded from https://packt.live/2YM9tAA.

Follow these steps to complete this exercise:

1. Create a new Jupyter Notebook – Exercise2.03.ipynb. We will be writing our code in this notebook.
2. Import the modules we will be using:

   # Import modules
   import cv2
   import numpy as np
   import matplotlib.pyplot as plt
   %matplotlib inline

3. Next, read the image.

   Note

   Before proceeding, be sure to change the path to the image (highlighted) based on where the image is saved in your system.

   The code is as follows:

   img = cv2.imread("../data/book.jpg")

4. Display the image using Matplotlib, as follows:

   plt.imshow(img[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.25: Output image of a book

5. Specify four points in the image so that they lie at the four corners of the front cover. Since we just want the front cover, the output points will be nothing but the corner points of the final 300×300 image. Note that the order of the points should stay the same for both the input and output points:

   inputPts = np.float32([[4,381],
                         [266,429],
                         [329,68],
                         [68,20]])
   outputPts = np.float32([[0,300],
                          [300,300],
                          [300,0],
                          [0,0]])

6. Next, obtain the transformation matrix:

   M = cv2.getPerspectiveTransform(inputPts,outputPts)

7. Apply this transformation matrix to carry out perspective transformation:

   dst = cv2.warpPerspective(img,M,(300,300))

8. Display the resultant image using Matplotlib. The X and Y axes refer to the width and height of the image, respectively:

   plt.imshow(dst[:,:,::-1])
   plt.show()

   

Figure 2.26: Front cover of the book

In this exercise, we saw how we can use geometric transformations to extract the front cover of the book provided in a given image. This can be interesting when we are trying to scan a document and we want to obtain a properly oriented image of the document after scanning.

Note

To access the source code for this specific section, please refer to https://packt.live/2YOqs5u.

With that, we have covered all the major geometric transformations. It's time to cover another important topic in image processing – image arithmetic.

We know that images are nothing but matrices. This raises an important and interesting question. If we can carry out arithmetic operations on matrices, can we carry them out on images as well? The answer is a bit tricky. We can carry out the following operations on images:

• Adding and subtracting two images
• Adding and subtracting a constant value to/from image
• Multiplying a constant value by an image

We can, of course, multiply two images if we can assume they're matrices, but in terms of images, multiplying two images does not make much sense, unless it's carried out pixel-wise.

Let's look at these operations, one by one.

Image Addition

We know that an image is made up of pixels and that the color of a pixel is decided by the pixel value. So, when we talk about adding a constant to an image, we mean adding a constant to the pixel values of the image. While it might seem a very simple task, there is a small concept that needs to be discussed properly. We have already said that, usually, the pixel values in images are represented using unsigned 8-bit integers, and that's why the range of pixel values is from 0 to 255. Now, imagine that you want to add the value 200 to an image, that is, to all the pixels of the image. If we have a pixel value of 220 in the image, the new value will become 220 + 200 = 420. But since this value lies outside of the range (0-255), two things can happen:

• The value will be clipped to a maximum value. This means that 420 will be revised to 255.
• The value will follow a cyclic order or a modulo operation. A modulo operation means that you want to find the remainder obtained after dividing one value by another value. We are looking at division by 255 here (the maximum value in the range). That's why 420 will become 165 (the remainder that's obtained after dividing 420 by 255).

Notice how the results obtained in both approaches are different. The first approach, which is also the recommended approach, uses OpenCV's cv2.add function. The usage of the cv2.add function is as follows:

dst = cv2.add(src1, src2)

The second approach uses NumPy while adding two images. The NumPy approach is as follows:

dst = src1 + src2

src1 refers to the first image that we are trying to add to the second image (src2). This gives the resultant image (dst) as the output. Either of these approaches can be used to add two images. The interesting part, as we will see shortly in the next exercise, is that when we add a constant value to an image using OpenCV, by default, that value gets added to the first channel of the image. Since we already know that images in OpenCV are represented in BGR mode, the value gets added to the blue channel, giving the image a more bluish tone. On the other hand, in the NumPy approach, the value is automatically broadcasted in such a manner that the value is added to every channel.

Let's compare both approaches with the help of an exercise.

Exercise 2.04: Performing Image Addition

In this exercise, we will learn how to add a constant value to an image and the approaches to carry out the task. We will be working on the following image. First, we will add a constant value to the image using the cv2.add function and then compare the output obtained with the output obtained by adding the constant value using NumPy:

Figure 2.27: Image of a Golden Retriever puppy

Note

This image can be found at https://packt.live/2ZnspEU.

Follow these steps to complete this exercise:

1. Create a new notebook – Exercise2.04.ipynb. We will be writing our code in this notebook.
2. Let's import the libraries we will be using and also write the magic command:

   # Import libraries
   import cv2
   import numpy as np
   import matplotlib.pyplot as plt
   %matplotlib inline

3. Read the image. The code for this is as follows:

   Note

   Before proceeding, be sure to change the path to the image (highlighted) based on where the image is saved in your system.

   # Read image
   img = cv2.imread("../data/puppy.jpg")

4. Display the image using Matplotlib:

   # Display image
   plt.imshow(img[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.28: Image of a Golden Retriever puppy

5. First, try adding the value 100 to the image using NumPy:

   # Add 100 to the image
   numpyImg = img+100

6. Display the image, as follows:

   # Display image
   plt.imshow(numpyImg[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.29: Result obtained by adding 100 to the image using NumPy

   Notice how adding the value 100 has distorted the image severely. This is because of the modulo operation being performed by NumPy on the new pixel values. This should also give you an idea of why NumPy's approach is not the recommended approach to use while dealing with adding a constant value to an image.

7. Try doing the same using OpenCV:

   # Using OpenCV
   opencvImg = cv2.add(img,100)

8. Display the image, as follows:

   # Display image
   plt.imshow(opencvImg[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.30: Result obtained by adding 100 to the image using OpenCV

   As shown in the preceding figure, there is an increased blue tone to the image. This is because the value 100 has only been added to the first channel of the image, which is the blue channel.

9. Fix this by adding an image to an image instead of adding a value to an image. Check the shape, as follows:

   img.shape

   The output is (924, 1280, 3).

10. Now, create an image that's the same shape as the original image that has a fixed pixel value of 100. We are doing this because we want to add the value 100 to every channel of the original image:

    nparr = np.ones((924,1280,3),dtype=np.uint8) * 100

11. Add nparr to the image and visualize the result:

    opencvImg = cv2.add(img,nparr)
    # Display image
    plt.imshow(opencvImg[:,:,::-1])
    plt.show()

    The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

    

    Figure 2.31: Result obtained by adding an image to another image

12. When the same image is added using OpenCV, we notice that the results that are obtained are the same as they were for NumPy:

    npImg = img + nparr
    # Display image
    plt.imshow(npImg[:,:,::-1])
    plt.show()

    The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

    

Figure 2.32: New results obtained

The most interesting point to note from the results is that adding a value to an image using OpenCV results in increased brightness of the image. You can try subtracting a value (or adding a negative value) and see whether the reverse also true.

In this exercise, we added a constant value to an image and compared the outputs obtained by using the cv2.add function and by using NumPy's addition operator (+). We also saw that while using the cv2.add function, the value was added to the blue channel and that it can be fixed by creating an image that's the same shape as the input image, with all the pixels of the value equal to the constant value we want to add to the image.

Note

To access the source code for this specific section, please refer to https://packt.live/2BUOUsV.

In this section, we saw how to perform image addition using NumPy and OpenCV's cv2.add function. Next, let's learn how to multiply an image with a constant value.

Image Multiplication

Image multiplication is very similar to image addition and can be carried out using OpenCV's cv2.multiply function (recommended) or NumPy. OpenCV's function is recommended because of the same reason as we saw for cv2.add in the previous section.

We can use the cv2.multiply function as follows:

dst = cv2.Mul(src1, src2)

Here, src1 and src2 refer to the two images we are trying to multiply and dst refers to the output image obtained by multiplication.

We already know that multiplication is nothing but repetitive addition. Since we saw that image addition had an effect of increasing the brightness of an image, image multiplication will have the same effect. The difference here is that the effect will be manifold. Image addition is typically used when we want to make minute modifications in brightness. Let's directly see how to use these functions with the help of an exercise.

Exercise 2.05: Image Multiplication

In this exercise, we will learn how to use OpenCV and NumPy to multiply a constant value with an image and how to multiply two images.

Note

The image used in this exercise can be found at https://packt.live/2ZnspEU.

Follow these steps to complete this exercise:

1. Create a new notebook – Exercise2.05.ipynb. We will be writing our code in this notebook.
2. First, let's import the necessary modules:

   # Import libraries
   import cv2
   import numpy as np
   import matplotlib.pyplot as plt
   %matplotlib inline

3. Next, read the image of the puppy.

   Note

   Before proceeding, be sure to change the path to the image (highlighted) based on where the image is saved in your system.

   The code for this is as follows:

   # Read image
   img = cv2.imread("../data/puppy.jpg")

4. Display the output using Matplotlib, as follows:

   # Display image
   plt.imshow(img[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.33: Image of a Golden Retriever puppy

5. Multiply the image by 2 using the cv2.multiply function:

   cvImg = cv2.multiply(img,2)

6. Display the image, as follows:

   plt.imshow(cvImg[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.34: Result obtained by multiplying the image by 2 using OpenCV

   Can you think of why you obtained a high blue tone in the output image? You can use the explanation given for image addition in the previous exercise as a reference.

7. Try to multiply the image using NumPy:

   npImg = img*2

8. Display the image, as follows:

   plt.imshow(npImg[:,:,::-1])
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.35: Result obtained by multiplying the image by 2 using NumPy

9. Print the shape of the image, as follows:

   img.shape

   The shape is (924, 1280, 3).

10. Now, let's create a new array filled with 2s that's the same shape as the original image:

    nparr = np.ones((924,1280,3),dtype=np.uint8) * 2

11. Now, we will use this new array for multiplication purposes and compare the results that are obtained:

    cvImg = cv2.multiply(img,nparr)
    plt.imshow(cvImg[:,:,::-1])
    plt.show()

    The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

    

Figure 2.36: Result obtained by multiplying two images using OpenCV

Note

To access the source code for this specific section, please refer to https://packt.live/2BRos3p.

We know that multiplication is nothing but repetitive addition, so it makes sense to obtain a brighter image using multiplication since we obtained a brighter image using addition as well.

So far, we've discussed geometric transformations and image arithmetic. Now, let's move on to a slightly more advanced topic regarding performing bitwise operations on images. Before we discuss that, let's have a look at binary images.

So far, we have worked with images with one channel (grayscale images) and three channels (color images). We also mentioned that, usually, pixel values in images are represented as 8-bit unsigned integers and that's why they have a range from 0 to 255. But that's not always true. Images can be represented using floating-point values and also with lesser bits, which also reduces the range. For example, an image using 6-bit unsigned integers will have a range between 0 - (26-1) or 0 to 63.

Even though it's possible to use more or fewer bits, typically, we work with only two kinds of ranges – 0 to 255 for 8-bit unsigned integers and images that have only 0 and 1. The second category of images uses only two pixel values, and that's why they are referred to as binary images. Binary images need only a single bit to represent a pixel value. These images are commonly used as masks for selecting or removing a certain region of an image. It is with these images that bitwise operations are commonly used. Can you think of a place where you have seen binary images in real life?

You can find such black-and-white images quite commonly in QR codes. Can you think of some other applications of binary images? Binary images are extensively used for document analysis and even in industrial machine vision tasks. Here is a sample binary image:

Figure 2.37: QR code as an example of a binary image

Now, let's see how we can convert an image into a binary image. This technique comes under the category of thresholding. Thresholding refers to the process of converting a color image into a binary image. There is a wide range of thresholding techniques available, but here, we will focus only on a very simple thresholding technique – binary thresholding – since we are working with binary images.

The concept behind binary thresholding is very simple. You choose a threshold value and all the pixel values below and equal to the threshold are replaced with 0, while all the pixel values above the threshold are replaced with a specified value (usually 1 or 255). This way, you end up with an image that has only two unique pixel values, which is what a binary image is.

We can convert an image into a binary image using the following code:

# Set threshold and maximum value
thresh = 125
maxValue = 255
# Binary threshold
th, dst = cv2.threshold(img, thresh, maxValue, \
                        cv2.THRESH_BINARY)

In the preceding code, we first specified the threshold as 125 and then specified the maximum value. This is the value that will replace all the pixel values above the threshold. Finally, we used OpenCV's cv2.threshold function to perform binary thresholding. This function takes the following inputs:

• The grayscale image that we want to perform thresholding on.
• thresh: The threshold value.
• maxValue: The maximum value, which will replace all pixel values above the threshold.
• th, dst: The thresholding flag. Since we are performing binary thresholding, we will use cv2.THRESH_BINARY.

Let's implement what we've learned about binary thresholding.

Exercise 2.06: Converting an Image into a Binary Image

In this exercise, we will use binary thresholding to convert a color image into a binary image. We will be working on the following image of zebras:

Figure 2.38: Image of zebras

Note

This image can be found at https://packt.live/2ZpQ07Z .

Follow these steps to complete this exercise:

1. Create a new Jupyter Notebook – Exercise2.06.ipynb. We will be writing our code in this notebook.
2. Import the necessary modules:

   # Import modules
   import cv2
   import numpy as np
   import matplotlib.pyplot as plt
   %matplotlib inline

3. Read the image of the zebras and convert it into grayscale. This is necessary because we know that thresholding requires us to provide a grayscale image as an argument.

   Note

   Before proceeding, be sure to change the path to the image (highlighted) based on where the image is saved in your system.

   The code for this is as follows:

   img = cv2.imread("../data/zebra.jpg")
   img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

4. Display the grayscale image using Matplotlib:

   plt.imshow(img, cmap='gray')
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.39: Image in grayscale

5. Use the cv2.thresholding function and set the threshold to 150:

   # Set threshold and maximum value
   thresh = 150
   maxValue = 255
   # Binary threshold
   th, dst = cv2.threshold(img, thresh, maxValue, \
                           cv2.THRESH_BINARY)

   Note

   You can try playing around with the threshold value to obtain different results.

6. Display the binary image we have obtained:

   plt.imshow(dst, cmap='gray')
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

Figure 2.40: Binary image

Note

To access the source code for this specific section, please refer to https://packt.live/2VyYHfa.

In this exercise, we saw how to obtain a binary image using thresholding. Next, let's see how we can carry out bitwise operations on these images.

Bitwise Operations on Images

Let's start by listing the binary operations, along with their results. You must have read about these operations before, so we won't go into their details. The following table provides the truth tables for the bitwise operations as a quick refresher:

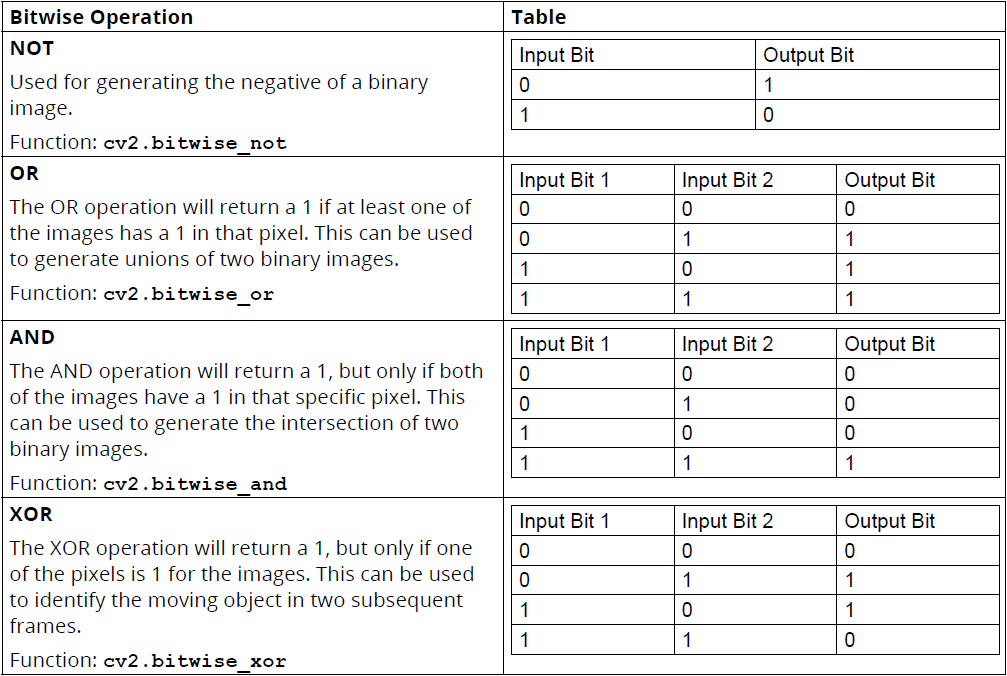
Figure 2.41: Bitwise operations and truth tables

Let's see how we can use these functions with the help of an exercise.

Exercise 2.07: Chess Pieces

In this exercise, we will use the XOR operation to find the chess pieces that have moved using two images taken of the same chess game:

Figure 2.42: Two images of chess board

Note

These images can be found at https://packt.live/3fuxLoU.

Follow these steps to complete this exercise:

1. Create a new notebook – Exercise2.07.ipynb. We will be writing our code in this notebook.
2. Import the required modules:

   # Import modules
   import cv2
   import numpy as np
   import matplotlib.pyplot as plt
   %matplotlib inline

3. Read the images of the board and convert them to grayscale.

   Note

   Before proceeding, be sure to change the path to the images (highlighted) based on where the images are saved in your system.

   The code for this is as follows:

   img1 = cv2.imread("../data/board.png")
   img2 = cv2.imread("../data/board2.png")
   img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
   img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)

4. Display these images using Matplotlib:

   plt.imshow(img1,cmap="gray")
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.43: Grayscale version of the chess image

5. Plot the second image, as follows:

   plt.imshow(img2,cmap="gray")
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.44: Grayscale version of the chess image

6. Threshold both the images using a threshold value of 150 and a maximum value of 255:

   # Set threshold and maximum value
   thresh = 150
   maxValue = 255
   # Binary threshold
   th, dst1 = cv2.threshold(img1, thresh, maxValue, \
                            cv2.THRESH_BINARY)
   # Binary threshold
   th, dst2 = cv2.threshold(img2, thresh, maxValue, \
                            cv2.THRESH_BINARY)

7. Display these binary images using Matplotlib:

   plt.imshow(dst1, cmap='gray')
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.45: Binary image

8. Print the second image, as follows:

   plt.imshow(dst2, cmap='gray')
   plt.show()

   The output is as follows. The X and Y axes refer to the width and height of the image, respectively:

   

   Figure 2.46: Image after thresholding

9. Use bitwise XOR to find the pieces that have moved, as follows:

   dst = cv2.bitwise_xor(dst1,dst2)

10. Display the result, as follows. The X and Y axes refer to the width and height of the image, respectively:

    plt.imshow(dst, cmap='gray')
    plt.show()

    The output is as follows:

    

Figure 2.47: Result of the XOR operation

Notice that, in the preceding image, the four pieces that are present show the initial and final positions of the only two pieces that had changed their positions in the two images. In this exercise, we used the XOR operation to perform motion detection to detect the two chess pieces that had moved their positions after a few steps.

Note

To access the source code for this specific section, please refer to https://packt.live/2NHixQY.

Masking

Let's discuss one last concept related to binary images. Binary images are quite frequently used to serve as a mask. For example, consider the following image. We will be using an image of a disk:

Figure 2.48: Image of a disk

After image thresholding, the mask will look as follows:

Figure 2.49: Binary mask

Let's see what happens when we apply masking to the image of the zebras that we worked with earlier:

Figure 2.50: Image of zebras

The final image will look as follows:

Figure 2.51: Final image

Let's start with Figure 2.49. This image is a binary image of a disk after thresholding. Figure 2.50 shows the familiar grayscale image of zebras. When Figure 2.49 is used as a mask to only keep the pixels of Figure 2.50, where the corresponding pixels of Figure 2.50 are white, we end up with the result shown in Figure 2.51. Let's break this down. Consider a pixel, P, at location (x,y) in Figure 2.49. If the pixel, P, is white or non-zero (because zero refers to black), the pixel at location (x,y) in Figure 2.50 will be left as it is. If the pixel, P, was black or zero, the pixel at location (x,y) in Figure 2.50 will be replaced with 0. This refers to a masking operation since Figure 2.49 is covering Figure 2.50 as a mask and displaying only a few selected pixels. Such an operation can be easily carried out using the following code:

result = np.where(mask, image, 0)

Let's understand what is happening here. NumPy's np.where function says that wherever the mask (first argument) is non-zero, return the value of the image (second argument); otherwise, return 0 (third argument). This is exactly what we discussed in the previous paragraph. We will be using masks in Chapter 5, Face Processing in Image and Video, as well.

Now, it's time for you to try out the concepts that you have studied so far to replicate the result shown in Figure 2.51.

Activity 2.01: Masking Using Binary Images

In this activity, you will be using masking and other concepts you've studied in this chapter to replicate the result shown in Figure 2.51. We will be using image resizing, image thresholding, and image masking concepts to display only the heads of the zebras present in Figure 2.50. A similar concept can be applied to create nice portraits of photos where only the face of the person is visible and the rest of the region/background is blacked out. Let's start with the steps that you need to follow to complete this activity:

1. Create a new notebook – Activity2.01.ipynb. You will be writing your code in this notebook.
2. Import the necessary libraries – OpenCV, NumPy, and Matplotlib. You will also need to add the magic command to display images inside the notebook.
3. Read the image titled recording.jpg from the disk and convert it to grayscale.

   Note

   This image can be found at https://packt.live/32c3pDK.

4. Next, you will have to perform thresholding on this image. You can use a threshold of 150 and a maximum value of 255.
5. The thresholded image should be similar to the one shown in Figure 2.49.
6. Next, read the image of the zebras (titled zebras.jpg) and convert it to grayscale.

   Note

   This image can be found at https://packt.live/2ZpQ07Z.

7. Before moving on to using NumPy's where command for masking, we need to check whether the images have the same size or not. Print the shapes of both images (zebras and disk).
8. You will notice that the images have different dimensions. Resize both images to 1,280×800 pixels. This means that the width of the resized image should be 1,280 pixels and that the height should be 800 pixels. You will have to use the cv2.resize function for resizing. Use linear interpolation while resizing the images.
9. Next, use NumPy's where command to only keep the pixels where the disk pixels are white. The other pixels should be replaced with black color.

By completing this activity, you will get an output similar to the following:

Figure 2.52: Zebra image

The result that we have obtained in this activity can be used in portrait photography, where only the subject of the image is highlighted and the background is replaced with black.

Note

The solution for this activity can be found via this link.

By completing this activity, you have learned how to use image resizing to change the shape of an image, image thresholding to convert a color image into a binary image, and bitwise operations to perform image masking. Notice how image masking can be used to "mask" or hide certain regions of an image and display only the remaining portion of the image. This technique is used extensively in document analysis in computer vision.

In this chapter, we started by understanding the various geometric transforms and their matrix representations. We also saw how we can use OpenCV's functions to carry out these transformations. Then, we performed arithmetic operations on images and saw how addition and multiplication with a constant can be understood as a brightening operation. Next, we discussed binary images and how they can be obtained using binary thresholding. Then, we discussed bitwise operations and how they can be carried out using OpenCV. Finally, we had a look at the concept of masking, where we used NumPy to obtain interesting results.

In the next chapter, we will jump into the world of histograms and discuss how we can use histogram matching and histogram equalization as more advanced image processing steps.