The focus of this chapter is on establishing a link between the languages and library features of modern C++. Some familiarity with C++ is assumed, but we try to explain more modern features that you might not have encountered before. There are some exercises associated with this chapter found in the Chapter-02 folder of the GitHub repository for this book: https://github.com/PacktPublishing/The-CPP-Programmers-Mindset. Some snippets of code also have tests in this repository.

Before we start, we need to have some understanding of the different categories of problems. This is important because it forms part of the context in which we formulate our abstractions and thus guides our choices of how to implement solutions. All problems can be broken down into a set of basic problems via a sequence of reductions. These basic problems are those that you probably already know how to solve – for instance, using classic data structures and algorithms. As you gain experience, fewer reductions will be needed in most cases, and you will recognize problems that are of increasing complexity and know how to solve these. Very broadly, basic problems fall into one of four domains, at least for the purposes of this discussion, each with numerous subcategories and some overlapping concepts:

• Combinatorial problems, including sorting and searching
• Input-output (IO) problems, and interacting with the host system
• Numerical problems, including generating random numbers
• Interface problems, including interacting with users

Combinatorial problems are those that involve counting, sorting (or otherwise rearranging), searching (for a single value or a range of values), otherwise combining elements in a range, and graph problems. This describes a very large and generally well-understood branch of computer science, encompassing most classic data structures and algorithm courses. There are excellent algorithms for identifying common substrings or finding instances of a particular pattern within a string (regular expressions). This also includes tasks such as route finding (or graph traversal). Most of the simple examples of problems in this category include finding or sorting simple linear data – data that can be naturally placed in a line without losing contextual information. However, it also covers problems that are not so simple. Finding a route in two- or three-dimensional space, navigating around obstacles in the environment, is one such example (using the A* algorithm, for example).

Input-output problems are those that involve finding and loading data to be processed, such as locating the file on a disk and loading it into a sequence of bytes within the program’s address space, where it can be accessed directly, or the reverse. Most (if not all) operating systems include a sophisticated file system, which allows users and programs operating in user space on the computer to locate data on disk. (This is itself a great example of how abstractions can be used.) Files provide an interface that allows the program to obtain the data. Data might not be located on disk; it could be located on another device reached by a network connection, or it might not exist anywhere (for instance, a sensor that is constantly transmitting readings). Obtaining data from these sources can be trickier, especially if it is ephemeral. Once the program has finished its processing of the input data, it will need to store or otherwise display the results. This category also includes problems involving moving data between devices on the same system, such as moving data to a GPU and initiating a computation (though the nature of the computation is very likely to be of the next category).

Numerical problems are those that are inherently mathematical: performing calculations directly on data; encoding/decoding (or encrypting/decrypting) data; solving optimization problems; statistical analysis or inference; and many others. These problems appear everywhere – have you ever wondered how video streaming services derive suggestions for you? It can be quite tricky to identify numerical problems “in the wild.” This is primarily because of the breadth of this category, and because there is usually some additional work to be done to understand a problem within this general category. It takes some thinking to turn a recommendation problem into a problem of linear algebra. Recognizing the numerical aspects of a problem and identifying the requirements within the data and the feasibility of the final results are part of this process.

Interface problems are slightly different, somewhat related to the IO problems, although far different in purpose. This category concerns how other users or programs will interact with your solution. Is this a simple command-line application? Is it a programmatic interface (API)? Is it a website? Each of these involves a set of (related) challenges. This is an essential component of all programming-related problems; if nobody can interact with your solution to the problem, then it doesn’t really exist. Sometimes this challenge is obscured because you’re adding new functionality to software that already has a well-defined interface, but it is still there and demands attention. A poorly implemented interface can mean the program is unusable, will break frequently, or will become difficult to maintain.

Abstraction is the primary mechanism for enabling one to realize a complex problem as one or more basic problems. The nature of the abstraction depends on the problem and the basic categories that it intersects with. For instance, for categorical problems, we might typically look for abstractions in the data and operations. The algorithm for sorting is identical, regardless of whether the ordering is done by less-than or greater-than. For IO-type problems, the abstractions typically arise around the interface between the program and the operating system of the computer, and potentially around the form and format of the data. For numerical problems, the data and methodology are the likely abstraction pathways, possibly involving some transformation of input and outputs so that they can be operated upon numerically. (For instance, large language models operate on integer tokens and not strings containing words or letters.) For interface problems, the mechanism for interacting with the consumer is the abstraction. The functions and classes that make up the user interface hide the details of the actual implementation.

Connecting problems with C++ abstraction mechanisms

The C++ language and standard library contain many useful tools for delivering abstractions. The tricky part is understanding when and how to use these to solve problems; in essence, this is the topic of this book. The first step is, of course, to try and identify the broad categories outlined above that exist in the context of your problem. It’s safe to say that at least interfaces will be involved, and IO is also likely to be a component. Unless your problem is specifically an IO problem, it will almost surely involve at least one other category. (Identifying the different categories involved is, of course, a good way to start to decompose your problem into smaller parts.)

The C++ language provides several mechanisms for encapsulating and abstracting specific aspects of a program. For instance, it allows us to abstract a chain of operations used to transform input data into output data. They are themselves an encapsulation of this chain of operations, allowing a higher-level user to make use of the function to transform inputs to outputs without understanding the actual implementation.

This is a common pattern among language features; many of these are designed to encapsulate certain functionality so it can be reused or hidden from the user for other reasons (such as intellectual property protection). These mechanisms are primarily applicable for designing interfaces and interacting with libraries that implement solutions to some general problems (such as LAPACK for linear algebra).

Also included in the language are the powerful template and concept features. These mechanisms allow us to write a single piece of code that can be used for multiple C++ types. The compiler fills in the correct code at compile time for these types. Most of the C++ standard library is built around templates, so it can be used flexibly without requiring the library itself to contain compiled versions of the code for each possible combination of types. (Even this would not begin to approximate the flexibility of templates.) Concepts are the extension of the template system to allow the programmer to specify precisely the requirements of types passed into a template, primarily to aid debugging template code. Concepts are a great way to think about data and functionality. Each time you see a new problem, try to understand, from a conceptual point of view, what the requirements are. This is part of formulating an abstraction for your data (see the discussion in Chapter 1).

The C++ standard library is a collection of standard abstractions for specific tasks: working with the file system and interaction with files; storing data in various forms; working with basic mathematical operations (exp, log, etc.); working with text, strings, and regular expressions; standard algorithms; and many more. These are building blocks that help us interact with the system, the user, and with standard algorithms that appear commonly in programming problems. We already introduced the algorithm header in the previous chapter, and we will discuss it again in the next section. This contains implementations of many combinatorial algorithms (sorting and searching are the major ones). These function templates are extremely flexible and can be used anywhere these problems appear.

Input and output with C++

Most of the remainder of this chapter will be dedicated to using the C++ language and libraries to define, implement, and interface with solutions to some of the categories of problems. However, there is one aspect that is worth discussing before we dive into these details. This is the facility for loading (or otherwise “inputting”) data and saving, storing, or printing results. Most IO in C++ is handled using the “streams” interface, encapsulated in various headers such as iostream. Fundamentally, an (input) stream is some kind of object that allows the user to read one or more bytes in a structured or unstructured manner. (There are other requirements of an istream object, but these broadly support the read functionality.)

This interface is quite flexible and works very well for reading from files on disk (ifstream) or from the terminal (cin). It allows one to read raw bytes from the file, or to read structured data such as integers or floating-point numbers using the stream in operator >>. For example, the following block of code reads bytes from cin to construct a double.

double value;
std::cin >> value;

This makes the assumption that the current sequence of bytes defines a valid double value in the format we are expecting. (In this case, a sequence of digits exactly as we would have written in the code itself.) If this assumption fails, such as the byte pattern contains a letter ‘a’, then an error state is set (either by failbit or an exception, depending on the stream configuration). Of course, there are many ways that a double could be stored as a sequence of raw bytes – a textual representation is just one example. This topic is called serialization.

Serialization is the process of taking a value and producing a representation that can be stored, independent of the internal state of the program, can be loaded later, and “exactly” recover the value as it was. There are many different means of doing this; JSON, XML, and Protocol Buffers are all examples of formats for serializing complex objects into text or raw bytes that can be transmitted or stored and then loaded elsewhere. The stream interface of the standard library is far more primitive than this – most serialization libraries are built on top of this interface.

The reason for this diversion into IO is partly to explain how we can address those challenges when writing our code, but it is also a perfect demonstration of how stacking relatively simple abstractions can build very powerful tools for solving complicated problems. This is a concept that will appear many times within this book.

Algorithms are the bread and butter of programming and are a topic that we will describe in great detail in the next chapter. The standard algorithm headers are not algorithms as such, but instead are implementations of common (families of) algorithms for solving common abstract problems. (These mostly cover problems from classic data structure and algorithm courses from classic computer science.) They are surprisingly useful and turn up in lots of places. The power of these functions comes from their use of templates for every aspect of the operation: different search predicates, different comparisons and orderings, indirection, and projection.

As we have seen before, the real trick is finding places where these functions can be used, with simple operations or something more bespoke. Sometimes it can appear as if none of these functions are appropriate, until you frame the problem (via abstraction) in the correct way. This part of the standard library contains functions covering several categories of algorithms. The main ones are listed here.

• Search operation: Find an item in a range that satisfies some condition
• Copying operations: Copying or moving data around
• Transformation operations: Transforming the items in one range to another
• Permutations: Changing the order of items in a range
• Sorting and partitioning: Ordering items by a predicate and splitting a sorted range
• Binary searching: Searching but done faster using ordering
• Generating operations: Filling a range in various ways

The kind of reasoning required to put these functions to use effectively is very specific to the problem at hand. Sometimes this involves finding a means of (efficiently) iterating through your problem space or finding a proxy for the problem space that achieves this goal. Alternatively, it could mean finding the right predicate or ordering. This is best illustrated by example.

Iterating through the problem domain

Suppose you are tasked with designing a system to find the closest positive signal to a given position in a grid. The signal is defined by an intensity score that can be located using the grid position. For simplicity, let’s say the grid is a grid and the observer is in the center position. One approach is to search the entire grid, row by row, starting at the top left, and find all positive signals. Then we can perform a second step to find the signal that is closest to the start position. This will work quite well for modest-sized grids. However, if the grid is very large and the start position is not at the top left of the grid, then this is very wasteful. The code for this is as follows:

int dim_x = 5;
int dim_y = 5;
double compute_signal_intensity(int x, int y);
double detection_intensity = 5.0;
// A simple abstraction of a grid position
struct Pos {
    int x;
    int y;
};
std::vector<Pos> signals;
signals.reserve(dim_x*dim_y);
for (int y = 0; y < dim_y; ++y) {
    for (int x = 0; x < dim_x; ++x) {
        if (compute_signal_intensity(x, y) > detection_intensity) {
            signals.emplace_back(x, y);
        }
    }
}

Once we’ve found all the positive signals, we can use std::min_element with a custom ordering to find the closest signal to the start position.

Pos start {2, 2}; // middle of the grid
auto dist_to_start = [&start](const Pos& pos) {
    return std::max(std::abs(pos.x - start.x),
                    std::abs(pos.y - start.y));
auto ordering = [&dist_to_start](const Pos& a, const Pos& b) {
    // a simple distance metric that will work nicely
    return dist_to_start(a) < dist_to_start(b);
}
auto closest_pos = std::min_element(signals, ordering);

This is a rather brute-force approach, and we’re not making use of any explicit abstraction, which leads to a functional but not efficient solution. The crucial information that we are forgetting is that the search is not global over the whole grid – we don’t care about signals that appear far away from the starting position unless there are none closer. Injecting a little abstraction and using a more appropriate algorithm will yield a better, more efficient, and more flexible approach that we can modify later.

Our goal is to make use of std::find, which is a much more appropriate algorithm, to find the first signal (which should be the closest one) and then terminate. We need to find a means of iterating outwards from the starting position. Let’s suppose that we have a range object that describes such an iteration, call it ExpandingSearchRange, and then we can find the closest position using the following very simple code.

auto predicate = [detection_intensity](int x, int y) {
    return compute_signal_intensity(x, y) > detection_intensity;
}
ExpandingSearchRange range(pos_x, pos_y);
auto closest_pos = std::ranges::find(range, predicate);

Assuming ExpandingSearchRange behaves as expected, this is guaranteed to find the closest signal position to the start (pos_x, pos_y). Since this terminates when it finds the first position at which the predicate function returns true, the expected number of evaluations of compute_signal_intensity is dramatically smaller than the dim_x*dim_y guaranteed evaluations from our first attempt. Moreover, should our objectives change or if additional constraints are imposed, we can simply swap ExpandingSearchRange with a modified version that meets the updated criteria.

We won’t implement ExpandingSearchRange here, but you should think about how this might be implemented. In the next section, we’ll look in more detail at how best to use functions (and function-like objects) both to segregate parts of the algorithm and as part of the abstraction itself.

Functions encapsulate a unit of computation and are most often used to allow that unit of computation to be used in many places. In their pure form, they operate on one or more input values to produce one or more output values. (Of course, C++ functions can only have a single return value, but we’ll come back to this.) The term “pure” means that the function itself is independent of the global program state; only the input data has any effect on the outputs. Non-pure functions have their uses too, but are far less easy to reason about. For this reason, we shall mostly restrict our attention to pure functions here.

Pure functions are a mathematical concept, defined as a relation between two sets under which each member of the “input” set is related to exactly one element of the “output” set (the codomain). That is, any given configuration of inputs should always produce the same output. This is obviously a very general concept, but keeping this in mind is a good reminder of how these should be used. A function should represent a single computation, which might be a numerical calculation or something more general, and return its result.

As we mentioned, C++ functions can only return a single value, but this does not mean that multiple values cannot be returned. For instance, we could make use of aggregate objects such as std::pair or std::tuple to package multiple values into a single object that can be returned, or we could adopt a more C-like approach in which the result is written to one or more addresses passed as pointer arguments. Both approaches have their uses. C++ functions are also unlike their mathematical inspiration because they might fail to complete their calculation for various reasons. In mathematics, the domain of a function can be limited by any number of constraints, whereas C++ can only limit function arguments by type; checking values must be done at runtime, leading to errors.

A function can also be thought of as a means of hiding actual implementation details from the wider program. They are a very low-cost (especially if inlined) means of abstracting particular details such as a distance function between points, an ordering or other comparison, or a predicate function for searching. Functions should be used to logically structure implementations and as a means of providing flexibility for the problem domain. For instance, in the previous section, compute_signal_intensity might have several possible implementations that would yield different search characteristics.

Creating interfaces based on functions

One of the most important uses of functions is as the main interface for your code for external users (library consumers or directly via a GUI or other interface). The advantage of a function is that it is a simple concept that transfers well across boundaries. For instance, C++ functions can be made to use C calling conventions, making them usable from other languages that know how to call C-style functions. (Many languages have the capability to link against libraries compiled in C and use the functions.) Once inside the interface function, you’re free to make use of any of the mechanisms at your disposal to actually implement your solution.

Functions are a good way to define your interface because they are simple and easy to understand, but are still quite expressive. If one needs more complex functionality, one can make use of a more complex configuration object. This can be set with sensible defaults (depending on the problem, of course), so users who just need the basic functionality don’t need to spend a long time configuring. This is a remarkably flexible approach that has relatively small overheads in terms of runtime cost and overhead for the programmer.

Consider the following example. Suppose the problem is to load data from a selection of sources, provided by the user, and then produce a set of summary statistics (mean, standard deviation, min, max, etc.). A very simple interface might include a simple struct that contains the summary statistics, a single function that takes the sources as a sequence of strings describing where to find the data (using uniform resource identifiers, for example), and a configuration that allows the user to customize the actual set of summary statistics produced. (We can’t omit these from the return struct, but we can simply not calculate them.) This could be defined as follows:

struct SummaryStatistics; // definition omitted, not really important
class Configuration {
    bool b_include_mean = true;
    bool b_include_std = true;
    // more fields with sensible defaults
public:
    bool include_mean() const noexcept { return b_include_mean; }
    void include_mean(bool setting) noexcept {
        b_include_mean = setting;
    } 
    // functions that the user can use to customize
};
std::vector<SummaryStatistics>
compute_statistics(const Configuration& config, std::span<const std::string> sources);

Notice that the Configuration object is entirely inline, but it is still part of the interface of the program. Indeed, if this class changes (by adding new settings, for instance), then the function would have to be recompiled and would likely break backwards compatibility.

There is a good argument for making your programming interface as minimal as possible, making use of inline functions or very simple classes to adapt more complex driver routines rather than exporting everything. (This might be ideal, but it will not always be feasible.)

Sometimes, functions will not be completely sufficient for describing the interface you need. In this case, you might have to turn to using a class-based interface. This has some advantages in terms of flexibility, but it does expose some additional details about the implementation that one might want to keep private (to maintain intellectual property, for instance). There are ways around this, but none of these are as simple as a function-based interface.

Functions as building blocks

Functions are very useful for solving combinatorial or numerical problems. Typically, these kinds of problems have several moving parts. At the outer level, there is typically some kind of driving operation that performs an iteration over the problem domain. Inside this driver is a computation aspect and a decision aspect. In a sorting problem, the computation involves comparing pairs of elements, and the decision is whether to swap the positions of the two elements. The same holds true in many numerical algorithms that involve collections of data. (Obviously, computations that operate on single numbers or small collections of numbers do not usually require such complexity.) Functions are ideal for isolating these aspects and making the final solution easier to understand.

For example, suppose we want to find the value of a real number 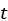at which some unknown (continuous) function 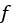obtains the value zero. One approach would be to use repeated bisection. This problem requires three pieces of information. The first is the (continuous) function itself, which takes a single argument and returns a single number; the second is a point in the domain at which the function takes a positive value; and the third is a value at which the function takes a negative value. We can implement the algorithm as follows:

#include <cmath>
// definitions of helper functions omitted
template <typename Function, typename Real>
Real find_root_bisect(Function&& function, Real pos, Real neg, Real tol)
{
    auto fpos = function(pos);
  
    // Driving loop
    while (compare_reals_equal(pos, neg)) {
        auto m = midpoint(pos, neg); // computes the midpoint (pos + neg)/2
        auto fm = function(m);
        // Quit early if the function is already (almost) 0.
        if (std::abs(fm) < tol) { return m; }
        // The decision logic to find the next point to check
        if (std::signbit(fm) == std::signbit(fpos)) {
            pos = m;
            fpos = fm;
        } else {
            neg = m;
        }
    }
    return fpos;
}

There are two “building block” functions in this implementation. The first (compare_reals_equal) is a function to determine whether two real numbers are distinguishable from one another – remember that C++ doubles only have a precision of approximately 15 decimal places (at best). The second function (midpoint) is used to compute the midpoint of the two given values. This isn’t strictly necessary here because computing the midpoint is so simple, but other similar algorithms use more complicated logic to determine which point should be checked next. Both of these building blocks could be replaced by more nuanced implementations that could change the characteristics of the iterative method. Keeping these as functions allows us to replace them more easily later (abstracting the algorithm), perhaps using additional template arguments and function-like objects (see the next section). At the very least, using functions here allows us to remain flexible as to the Real type. For instance, we might use a type that does not overload operator+ but works in the algorithm.

Let’s take a moment to understand the requirements of this algorithm. The first constraint is the mathematical requirements of the function. We require that the function takes a single real number, returns a single real number, is continuous – if one were to plot this function, the line would have no jumps – and that it has at least one positive value and at least one negative value. We cannot check that the function is continuous in the code.

The function will still run if this is not the case, but might not produce a meaningful answer (garbage in, garbage out); this is quite typical of numerical algorithms. The other conditions can be checked. For instance, we can check that the function is positive at one value and negative at the other rather simply, but we omit these checks in the preceding code to save space.

Function-like objects

In C++, we can define classes that have an operator() member function, which allows instances of the classes to be called like functions. These are surprisingly useful because they interact better with the template mechanism. (Function pointers cannot be meaningfully default-constructed, but function-like objects can.) The standard library contains several function-like objects in the functional header, including std::less and std::hash. These objects are used as default template parameters for containers such as std::map and std::unordered_map, and also in algorithms.

Function-like objects also include lambda functions, which are really syntactic sugar that the compiler turns into a class definition during compilation. Captured variables are just data members of this class that are injected into the call function body. Lambdas are a very useful means of declaring function-like objects. Our previous examples illustrate this perfectly.

More generally, callable classes can be used to represent functions that carry internal state (non-pure functions). A good example of where this is useful is if your function has some implicit random state. The class can maintain the random generator (e.g., std::mt19937) that is used to inject random state whenever the function is called. Here is an example.

#include <random>
class FunctionWithNoise {
    std::mt19937 m_rng;
    std::normal_distribution<double> m_dist;
public:
    double operator()(double arg) noexcept {
        auto noise = m_dist(m_rng);
        return 2.*arg + 1 + noise;
    }
};

Such a function would be useful in simulating data, where we need to generate large amounts of data that follows a known trend, but includes some randomly generated noise. For instance, this class could be useful for testing the performance of an inference pipeline.

Functions are very useful, but they are limited by the fact that they cannot usually hold state. Function objects can carry state, but this is a very poor reflection of the flexibility and power of fully object-oriented programming. In the next section, we will see how to make use of all the features of classes and inheritance to build truly flexible systems.

Classes are an encapsulation of data and behavior and should be used in one of two ways. The first is as a structured container that maintains some invariant property that can be used in and queried in algorithms using its methods (for example, std::vector<...>). The second use is as an abstract interface that hides the details, in a similar way to how functions can be used to hide implementation details. This allows you to write code against the abstract interface and use any object that implements it – for example, the IO stream interface in the C++ standard library. Both are examples of abstractions, but go about it in (somewhat) different ways.

When we talk about class-based abstract interfaces, we usually mean dynamic polymorphism (although that is not always the case). Polymorphism (literally translated as “many forms”) is a means by which a class (the interface) can be used in place of any class that implements its interface (the implementations). In C++, this is achieved with virtual functions; the pointers to the method implementations are placed in a lookup table that is queried at runtime to find the correct implementation to use. (Virtual functions are a very deep topic with decades of development and optimization, of which this barely scratches the surface. For more information, see https://en.wikipedia.org/wiki/Virtual_function and the references contained therein.) This has a small performance cost, but is very powerful.

Polymorphism, as described above, carries a performance cost at runtime. For this reason, we should avoid using polymorphic objects in the performance-critical portions of code where the added time to call a virtual function will accumulate quickly. On the other hand, using polymorphic objects on an interface boundary, especially those between a program and the user or with IO, can effectively hide the added cost of the function lookup. This makes polymorphic objects ideal for interacting with external concerns where the latency of the operation itself is the greatest cost.

Using classes to provide behavior for raw data

One of the basic ways to use a class is to encapsulate a structured set of data and behavior. The idea is that, in order to make use of some tools (such as std::find), the data must have some kind of standard interface (such as equality testable or equality comparable). For example, suppose that our problem is to examine an address book to find entries within a specific area. A basic entry in the address book might be as follows:

struct AddressBookRecord {
    size_t id;
    int house_number;
    std::string street_address;
    std::string city_and_state;
    int zip_code;
    // Other data fields that aren't relevant to the problem
};

Here, we use a struct so all these fields are visible to externally defined functions, but in practice, one would probably want to write accessor methods to hide these details from external users and prevent (or facilitate) modification. The id field is a unique identifier; every record must differ from every other by id. The other fields do not enjoy this property. This means we can write a very simple equality operator for these records as follows:

inline bool
operator==(const AddressBookRecord& lhs, const AddressBookRecord& rhs) noexcept
{
    return lhs.id == rhs.id;
}

Whilst id can be used to uniquely identify, it does not provide a useful ordering of the records. For this, one would need to look at the other listed fields. There are many different orderings to choose from. A reasonable choice is to order in reverse, starting with zip_code, then city_and_state, and so on, in dictionary-like ordering. (The implementation is quite long, so it is left as an exercise for you.) Of course, this might not be the specific ordering that you need for a given problem, and you might have to define others.

Unfortunately, operator< can only be implemented once, but anyway, naming these operators will help make the code more readable.

bool compare_house_humber(const AddressBookRecord&, const AddressBookRecord&);
bool compare_zip_code(const AddressBookRecord&, const AddressBookRecord&);

In this example, the class contains a copy of all the data, but this won’t always be desirable. Moving data around is expensive, so use lightweight views that contain a reference, which can be an actual reference (&), a pointer to the original (*), or a selection of views into certain fields of the data (e.g., string_view). All of these have their uses, but with the slight cost of a pointer indirection, at least in the first two cases. This can be used to implement a new interface on top of the raw data cheaply:

class RecordView {
    const AddressBookRecord* p_data;
public:
    size_t id() const noexcept { return p_data->id; }
    // constructors and other methods
}
inline bool operator==(const RecordView& lhs, const RecordView& rhs) noexcept
{
    return lhs.id() == rhs.id();
}

This approach has the added benefit that one can simply change the view type if different behavior is required. For instance, the interface can be changed if a different data ordering is required. The type system in C++ makes this slightly awkward, but it is sometimes useful.

Classes that represent physical objects

The other place that classes appear frequently is in object-oriented programming. Here, we use a combination of abstract interfaces that describe precisely the methods that must be provided, and implementations that give concrete realizations of one or more of these interfaces (we called this polymorphism in the introduction to this section). In this setup, consumers of the interfaces of the classes also have no need to know exactly how these interfaces are realized, only that they are. Interfaces can be stacked and combined, with some caveats that we won’t discuss here, to provide a rich ecosystem on which we can build functionality.

These hierarchies of classes and objects are often best utilized to describe physical objects (things that exist in the real world) or objects that live on the computer system (desktop windows, storage devices and files, etc.). Using polymorphism through class hierarchies has a real runtime cost, which makes them inefficient for working with raw data.

Physical objects, as described, all have far greater runtime costs that are much larger than the cost of the abstraction. For instance, a desktop window is redrawn each time the display refreshes, which might occur at 60Hz (60 times per second). This means the logic that is used to determine how a redraw should occur needs to take less than approximately 16 milliseconds, which is far greater than the cost of a virtual method lookup (at worst, a few microseconds).

Suppose our problem is to monitor a system of temperature sensors monitoring some equipment and raise an error. The temperature sensors might interact with the computer in different ways, or report temperatures in different formats. From our perspective, we need a raw temperature, in the form of a single float representing the temperature measurement in Kelvin (the SI unit for temperature). We will probably also need some kind of ID so we can provide some useful information to the user. Here’s what the interface might look like.

class TempSensor {
public:
    virtual ~TempSensor() = default;
    virtual std::string_view id() const noexcept = 0;
    virtual float temperature_kelvin() const noexcept = 0;
};

The two methods are pure virtual, so the implementation must provide both. To be explicit, and to help avoid confusion, use the name of the temperature function, including the units of measurement. This is a reminder to the programmer that, when adding new implementations, they should return Kelvin and not Fahrenheit or Celsius. The function that checks the sensors can be written easily in terms of this interface:

#include <format>
#include <span>
#include <stdexcept>
void check_sensors(std::span<const TempSensor*> sensors, float threshold) {
    for (const auto& sensor : sensors) {
        auto temp = sensor->temperature_kelvin();
        if (temp > threshold) {
            throw std::runtime_error(
                std::format("Sensor {} reports temperature {}",
                            sensor->id(), temp)
            );
        }
    }
}

This abstract interface makes the function very simple, and allows us to write code that doesn’t make use of information that we don’t need. (We only call the id method in the case that the temperature is above the threshold.) Interfaces should generally be sufficient and minimal to achieve the goals that they address. TempSensor satisfies both conditions; it does not require anything that isn’t used or provide anything that isn’t strictly necessary.

Classes and dynamic polymorphism come at the cost of runtime performance. This might not matter in some contexts, but in performance-critical sections, this extra overhead can be devastating. In the next section, see how we can make use of templates and concepts to perform static polymorphism that shifts the overhead to the compiler.

Templates are one of C++’s most powerful features, at least until C++26 brings first-class support for reflection. This mechanism allows the user to write code that uses placeholder types that are resolved during instantiation when the compiler sees a use of the template. As we described before, the template mechanism uses try first and unwind on failure. (This mechanism is often referred to as SFINAE or substitution failure is not an error – see https://en.cppreference.com/w/cpp/language/sfinae.html or [1].) Concepts work in a slightly different way. Here, the requirements should be listed up front and checked before the template is instantiated (at least in theory).

More importantly, templates and concepts are powerful abstraction mechanisms, allowing us to write code that works with many kinds of data or different algorithms, provided they broadly behave in the correct way (by exposing the correct methods, etc.). It’s quite rare that one starts writing code to solve a problem by writing template code, but thinking in terms of templates can sometimes help to find the correct formulation of an abstraction.

The right questions to ask are those such as: what methods need to exist, and what do I expect them to do? These are precisely the questions one should ask when extracting the relevant parts of a problem. We’ve seen an example of this already when we discussed standard algorithms. For example, std::find works for any “data” exposing a “forward range” interface, whose values can be evaluated by the predicate (such as to compare to a given value). We can look to similar properties in our data and in new problems.

Concepts force us to think about these properties up front. We can design our algorithms better if we put in the work up front to understand what the minimal set of requirements is to obtain the objectives. The main thing to understand is how one takes a problem from the problem domain and uses the features in C++ – in this context, templates and concepts – to realize these abstractions. We’ve already seen some examples of how functions from the algorithms header address structure in the problem itself.

Concepts for basic data

At the most basic level, a problem will involve some kind of basic unit of data. This might be something very simple, such as a single grid coordinate, or something more complex, such as a specific record in a database. Concepts allow us to create granular checks on the interface provided by a type at compile time, allowing us to more easily write generic algorithms.

For instance, let’s consider the Pos structure that we defined earlier. The x and y coordinates are integers because they describe a position in a grid. From the point of view of the algorithm, it only mattered that Pos had these two members, so we could write a concept to check that this condition was satisfied.

#include <concepts>
#include <type_traits>
template <typename T>
concept GridPosition = requires(T t) {
    std::is_same_v<decltype(t.x), int>;
    std::is_same_v<decltype(t.x), int>;
};

This concept will be satisfied whenever a type T has two members x and y that are both of type int. The code we wrote earlier could be replaced with generic code that uses this concept but operates in exactly the same way. This might be a little restrictive, because an int might not be large enough to contain the full extent of the grid. This is just a toy example to show what kind of checks are possible and is not intended to be practical.

More broadly, concepts can be used to check that types satisfy high-level requirements such as being ordered (see the std::totally_ordered concept), which would be a requirement for sorting algorithms, or being copyable or movable.

We can also check function-like objects to see whether they have the correct form. For instance, std::predicate tests whether the type is function-like and returns something convertible to a bool. There are also specific requirements, such as std::input_range, which we described in Chapter 1, and the related std::input_iterator.

When presented with a problem, it inevitably comes with some kind of data. This data might be something provided via some other part of the program (passed in a std::span, for instance), it could be something that you have to obtain from disk or elsewhere, or it could be something that is less well-defined. If it is a collection of data – such as records from a database – one has many concepts to think about. The first is the form of the collection, which one would hope is something range-like so one can iterate over it. (Different database drivers may provide different interfaces that do not require copying data several times.) Then we have to consider the individual records. In this situation, writing generic code with concepts might make your code easier to maintain later, if you decide to change the database driver, for instance.

Using traits to adapt behavior

We can also use templates to standardize or expand an interface without making extra additions to the type of an object itself. The standard library contains many examples of this. For instance, std::iterator_traits is a template that provides information about an iterator type, abstracting away the actual nature of the iterator itself. This allows us to implement algorithms that accept any iterator and make use of the traits object to query the provided type, rather than requiring a completely different template function for each kind of iterator. That being said, one might want to specialize for certain kinds of iterator for performance reasons. This mechanism can be thought of as the compile-time equivalent of abstract interface classes. They don’t incur a runtime-performance cost but instead take longer to compile.

Traits are obviously somewhat related to concepts. You might think of concepts as a subset of traits. Concepts are an extension of the template and type systems of C++. Traits are more complex since they generally are used to extend or modify the capabilities of a class based on a smaller interface or external factors.

This kind of facade can be used as a very lightweight means of interacting with plain data types such as the preceding AddressBookRecord. This is useful if different parts of the algorithm require that the data be interpreted in different ways (that are known at compile time) without requiring any explicit copy or conversion operations.

The more common use, however, is to act as a bridge between a fixed interface, which involves some set of types and functionality, and generic types that can be made to satisfy this interface. A generic interface for converting between types exactly is a good example here.

Suppose you are implementing a framework for performing exact conversions between numerical types. A 32-bit integer can be represented exactly as a double, since a double has 53 binary bits of precision, but a 64-bit integer cannot. The reverse is obviously never true. The C++ language allows for conversions between these types through simple static casts, but it makes no guarantees about exactness. Obviously, we can’t change the built-in types to implement safe conversions, so we can instead define a trait.

This trait takes the source and destination types as template arguments and implements the conversion only if it can be done exactly, and otherwise throws an exception. We might define the interface as follows:

template <typename From, typename To, typename=void>
struct ExactConversionTraits {
    using from_ref = const From&;
    using to_ref = To&;
    static void convert(to_ref to, from_ref from)
    {
        throw std::runtime_error("invalid exact conversion")
    }
};

The final template argument is to allow us to perform compile-time checks using the template parameters. For instance, we can implement conversion for integer types with a partial specialization of this template. Here, we use the std::intgeral concept to check whether both inputs are integers, but we could have used std::enable_if_t and std::is_integral_v in the final template argument to achieve the same effect (pre-C++20).

#include <concepts>
#include <limits>
template <std::integral From, std::integral To>
struct ExactConversionTraits<From, To>
{
    using from_ref = const From&;
    using to_ref = To&;
    static void convert(to_ref to, from_ref from) {
        if (from <= std::numeric_limits<To>::max
            && from >= std::numeric_limits<To>::min) {
            throw std::runtime_error("invalid exact conversion");
        }
        to = static_cast<To>(from);
    }
};

We can actually make this code much better by performing compile-time checks to remove unnecessary bounds checks at runtime. This will mean that the runtime cost of using this trait is zero if From is a 32-bit signed integer and To is a 64-bit signed integer, where the latter is guaranteed to exactly represent the former. We leave it as an exercise to specialize this trait for floating-point numbers.

The astute reader will have noticed that we seem to be doing something rather interesting with the signature of the convert function. Instead of taking a const From& argument and returning an instance of To, we instead take two reference arguments that are defined by member types in the trait. This is to accommodate types that might not be easily constructed, such as those that must be hidden behind a pointer. A concrete example of this is a GNU multi-precision (GMP) rational number mpq_t that is usually passed as a pointer, since it is implemented in C. Using this setup allows for greater flexibility than otherwise would be possible. Of course, there is nothing to stop you from extending the trait to include these other functions.

In this chapter, we examined the various abstraction mechanisms and standard algorithms that are provided by the C++ language and standard library. These serve two purposes in our pursuit of solutions to complex problems. The first is to help guide the way we formulate abstractions within the problem itself, such as identifying the critical properties and supported operations of the data. The second is to provide the possible routes that we might take and expose patterns and abstractions, and algorithms too, that we might look for in our problems. This accelerates the process of solving problems using computational thinking.

The standard library algorithms provide numerous high-quality and high-performance implementations of many combinatorial and numerical algorithms. These are generally encapsulated in template functions that make them extremely flexible and provide a very simple interface. Functions and classes form the basic building blocks of encapsulation and abstraction that can be used to tackle almost any problem. Templates and concepts increase these capabilities greatly and shift work to the compiler, further increasing runtime performance.

Now that we have a good understanding of abstraction mechanisms and how they can be applied in various situations, we can move on to understand more about algorithms and how to reason about them.

1. Vandevoorde, D., Josuttis, N.M. and Gregor, D. 2018. C++ templates: the complete guide. Boston, MA: Addison-Wesley.