Artificial Intelligence Concepts and Fundamentals
This chapter acts as a prelude to the entire book and the concepts within it. We will understand these concepts at a level high enough for us to appreciate what we will be building throughout the book.
We will start by getting our head around the general structure of Artificial Intelligence (AI) and its building blocks by comparing AI, machine learning, and deep learning, as these terms can be used interchangeably. Then, we will skim through the history, evolution, and principles behind Artificial Neural Networks (ANNs). Later, we will dive into the fundamental concepts and terms of ANNs and deep learning that will be used throughout the book. After that, we take a brief look at the TensorFlow Playground to reinforce our understanding of ANNs. Finally, we will finish off the chapter with thoughts on where to get a deeper theoretical reference for the high-level concepts of the AI and ANN principles covered in this chapter, which will be as follows:
- AI versus machine learning versus deep learning
- Evolution of AI
- The mechanics behind ANNs
- Biological neurons
- Working of artificial neurons
- Activation and cost functions
- Gradient descent, backpropagation, and softmax
- TensorFlow Playground
AI versus machine learning versus deep learning
AI is no new term given the plethora of articles we read online and the many movies based on it. So, before we proceed any further, let's take a step back and understand AI and the terms that regularly accompany it from a practitioner's point of view. We will get a clear distinction of what machine learning, deep learning, and AI are, as these terms are often used interchangeably:

AI is the capability that can be embedded into machines that allows machines to perform tasks that are characteristic of human intelligence. These tasks include seeing and recognizing objects, listening and distinguishing sounds, understanding and comprehending language, and other similar tasks.
Machine learning (ML) is a subset of AI that encompasses techniques used to make these human-like tasks possible. So, in a way, ML is what is used to achieve AI.
In essence, if we did not use ML to achieve these tasks, then we would actually be trying to write millions of lines of code with complex loops, rules, and decision trees.
ML gives machines the ability to learn without being explicitly programmed. So, instead of hardcoding rules for every possible scenario to a task, we simply provide examples of how the task is done versus how it should not be done. ML then trains the system on this provided data so it can learn for itself.
ML is an approach to AI where we can achieve tasks such as grouping or clustering, classifying, recommending, predicting, and forecasting data. Some common examples of this are classifying spam mail, stock market predictions, weather forecasting, and more.
Deep learning is a special technique in ML that emulates the human brain's biological structure and works to accomplish human-like tasks. This is done by building a network of neurons just like in the brain through an algorithmic approach using ANNs, which are stack of algorithms that can solve problems at human-like efficiency or better.
These layers are commonly referenced as deepnets (deep architectures) and each has a specific problem that it can be trained to solve. The deep learning space is currently at the cutting edge of what we see today, with applications such as autonomous driving, Alexa and Siri, machine vision, and more.
Throughout this book, we will be executing tasks and building apps that are built using these deepnets, and we will also solve use cases by building our very own deepnet architecture.
Evolution of AI
To appreciate what we can currently do with AI, we need to get a basic understanding of how the idea of emulating the human brain was born, and how this idea evolved to a point where we can easily solve tasks in vision and language with human-like capability through machines.
It all started in 1959 when a couple of Harvard scientists, Hubel and Wiesel, were experimenting with a cat's visual system by monitoring the primary visual cortex in the cat's brain.
The primary visual cortex is a collection of neurons in the brain placed at the back of the skull and is responsible for processing vision. It is the first part of the brain that receives input signals from the eye, very much like how a human brain would process vision.
The scientists started by showing complex pictures such as those of fish, dogs, and humans to the cat and observed its primary visual cortex. To their disappointment, they got no reading from the primary visual cortex initially. Consequently, to their surprise on one of the trials, as they were removing the slides, dark edges formed, causing some neurons to fire in the primary visual cortex:
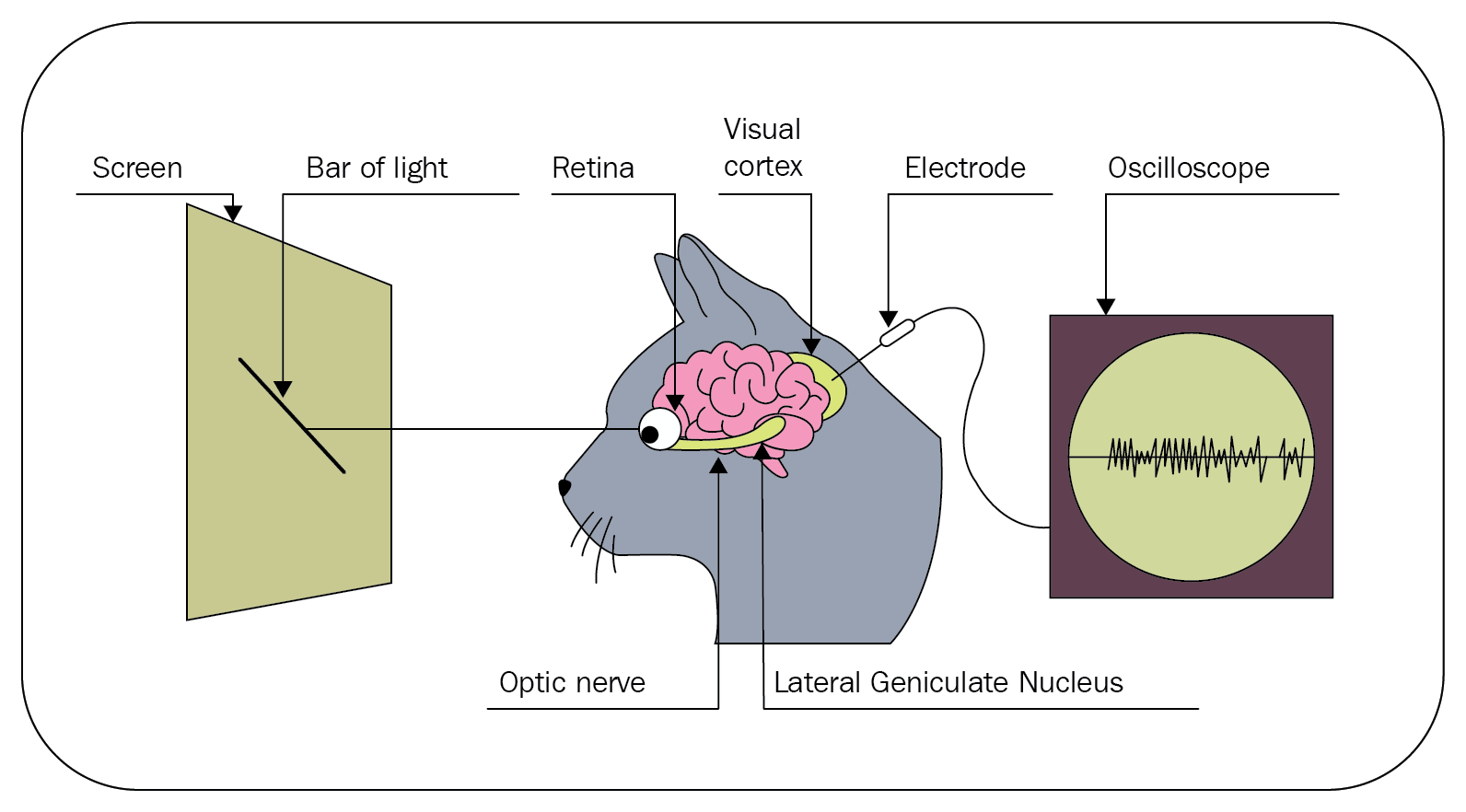
Their serendipitous discovery was that these individual neurons or brain cells in the primary visual cortex were responding to bars or dark edges at various specific orientations. This led to the understanding that the mammalian brain processes a very small amount of information at every neuron, and as the information is passed from neuron to neuron, more complex shapes, edges, curves, and shades are comprehended. So, all these independent neurons holding very basic information need to fire together to comprehend a complete complex image.
After that, there was a lull in the progress of how to emulate the mammalian brain until 1980, when Fukushima proposed neocognitron. Neocognitron is inspired by the idea that we should be able to create an increasingly complex representation using a lot of very simplistic representations – just like the mammalian brain!
The following is a representation of how neocognitron works, by Fukushima:
He proposed that to identify your grandmother, there are a lot of neurons that are triggered in the primary visual cortex, and each cell or neuron understands an abstract part of the final image of your grandmother. All of these neurons work in sequence, parallel, and tandem, and then finally hits a grandmother cell or neuron which fires only when it sees your grandmother.
Fast forward to today (2010-2018), with contributions from Yoshua Bengio, Yann LeCun, and Geoffrey Hinton, who are commonly known as the fathers of deep learning. They contribute massively to the AI space we work in today. They have given rise to a whole new approach to machine learning where feature engineering is automated.
The idea of not explicitly telling the algorithm what it should be looking for and letting it figure this out by itself by feeding it a lot of examples is the latest development. The analogy to this principle would be that of teaching a child to distinguish between an apple and an orange. We would show the child pictures of apples and oranges rather than only describing the two fruits' features, such as shape, color, size, and so on.
The following diagram shows the difference between ML and deep learning:
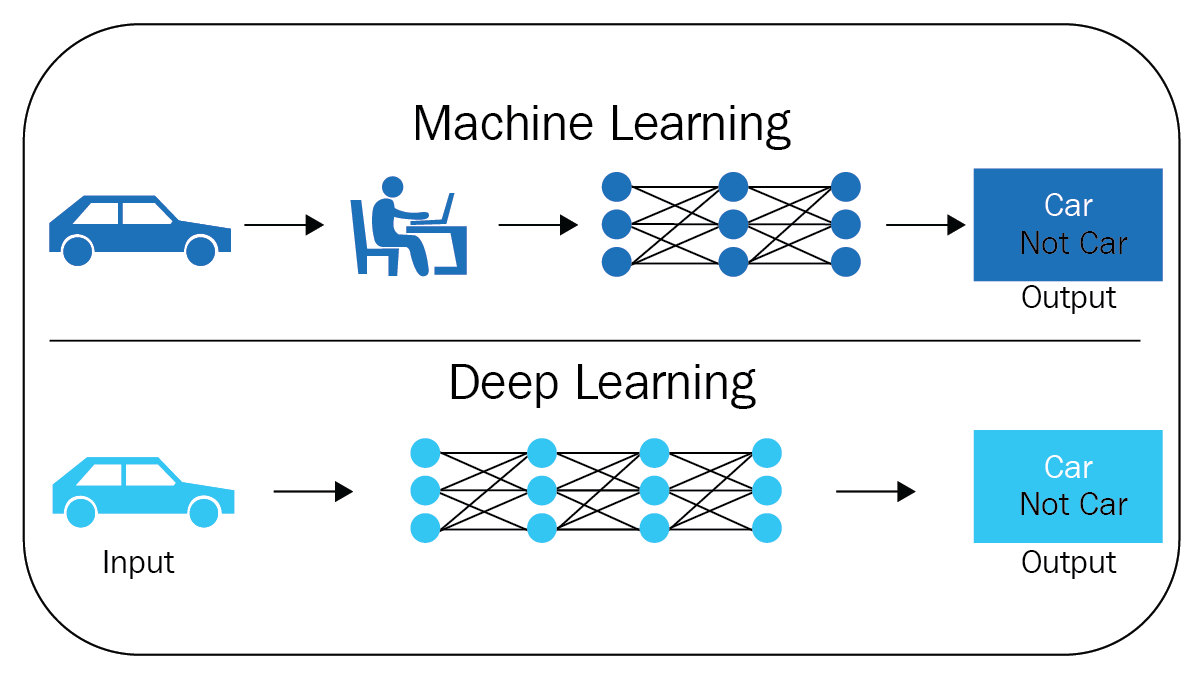
This is the primary difference between traditional ML and ML using neural networks (deep learning). In traditional ML, we provide features along with labels, but using ANNs, we let the algorithm decipher the features.
We live in an exciting time, an era we share with the fathers of deep learning, so much so that there are exchanges online in places such as Stack Exchange, where we can see contributions even from Yann LeCun and Geoffrey Hinton. This is analogous to living in the time of, and writing to, Nicholas Otto, the father of the internal combustion engine, who started the automobile revolution that we see evolving even to this day. The automobile revolution will be dwarfed by what could be possible with AI in the future. Exciting times, indeed!
The mechanics behind ANNs
In this section, we will understand the nuts and bolts that are required to start building our own AI projects. We will get to grips with the common terms that are used in deep learning techniques.
This section aims to provide the essential theory at a high level, giving you enough insight so that you're able to build your own deep neural networks, tune them, and understand what it takes to make state-of-the-art neural networks.
Biological neurons
We previously discussed how the biological brain has been an inspiration behind ANNs. The brain is made up of hundreds of billions of independent units or cells called neurons.
The following diagram depicts a neuron, and it has multiple inputs going into it, called dendrites. There is also an output going out of the cell body, called the axon:

The dendrites carry information into the neuron and the axon allows the processed information to flow out of the neuron. But in reality, there are thousands of dendrites feeding input into the neuron body as small electrical charges. If these small electrical charges that are carried by the dendrites have an effect on the overall charge of the body or cross over some threshold, then the axon will fire.
Now that we know how a biological neuron functions, we will understand how an artificial neuron works.
Working of artificial neurons
Just like the biological brain, ANNs are made up of independent units called neurons. Like the biological neuron, the artificial neuron has a body that does some computation and has many inputs that are feeding into the cell body or neuron:

For example, let's assume we have three inputs to the neuron. Each input carries a binary value of 0 or 1. We have an output flowing out of the body, which also carries a binary value of 0 or 1. For this example, the neuron decides whether I should eat a cake today or not. That is, the neuron should fire an output of 1 if I should eat a cake or fire 0 if I shouldn't:

In our example, the three inputs represent the three factors that determine whether I should eat the cake or not. Each factor is given a weight of importance; for instance, the first factor is I did cardio yesterday and it has a weight of 2. The second factor is I went to the gym yesterday and weighs 3. The third factor is It is an occasion for cake and weighs 6.
The body of the neuron does some calculation to inputs, such as taking the sum of all of these inputs and checking whether it is over some threshold:

So, for this example, let's set our threshold as 4. If the sum of the input weights is above the threshold, then the neuron fires an output of 1, indicating that I can eat the cake.
This can be expressed as an equation:

Here, the following applies:
- Xi is the first input factor, I did cardio yesterday.
- Wi is the weight of the first input factor, Xi. In our example, Wi = 2.
- Xii is the second input factor, I went to the gym yesterday.
- Wii is the weight of the second input factor, Xii. In our example, Wii = 3.
- Xiii is the third input factor, It is an occasion for cake.
- Wiii is the weight of the third input factor, Xiii. In our example, Wiii = 6.
- threshold is 4.
Now, let's use this neuron to decide whether I can eat a cake for three different scenarios.
Scenario 1
I want to eat a cake and I went to the gym yesterday, but I did not do cardio, nor is it an occasion for cake:

Here, the following applies:
- Xi is the first input factor, I did cardio yesterday. Now, Xi = 0, as this is false.
- Wi is the weight of the first input factor, Xi. In our example, Wi = 2.
- Xii is the second input factor, I went to the gym yesterday. Now, Xii = 1, as this is true.
- Wii is the weight of the second input factor, Xii. In our example, Wii = 3.
- Xiii is the third input factor, It is an occasion for cake. Now, Xiii = 0, as this is false.
- Wiii is the weight of the third input factor, Xiii. In our example, Wiii = 6.
- threshold is 4.
We know that the neuron computes the following equation:

For scenario 1, the equation will translate to this:

This is equal to this:

3 ≥ 4 is false, so it fires 0, which means I should not eat the cake.
Scenario 2
I want to eat a cake and it's my birthday, but I did not do cardio, nor did I go to the gym yesterday:

Here, the following applies:
- Xi is the first input factor, I did cardio yesterday. Now, Xi = 0, as this factor is false.
- Wi is the weight of the first input factor, Xi. In our example, Wi = 2.
- Xii is the second input factor, I went to the gym yesterday. Now, Xii = 0, as this factor is false.
- Wii is the weight of the second input factor, Xii. In our example, Wii = 3.
- Xiii is the third input factor, It is an occasion for cake. Now, Xiii = 1, this factor is true.
- Wiii is the weight of the third input factor, Xiii. In our example, Wiii = 6.
- threshold is 4.
We know that the neuron computes the following equation:

For scenario 2, the equation will translate to this:

It gives us the following output:

6 ≥ 4 is true, so this fires 1, which means I can eat the cake.
Scenario 3
I want to eat a cake and I did cardio and went to the gym yesterday, but it is also not an occasion for cake:

Here, the following applies:
- Xi is the first input factor, I did cardio yesterday. Now, Xi = 1, as this factor is true.
- Wi is the weight of the first input factor, Xi. In our example, Wi = 2.
- Xii is the second input factor, I went to the gym yesterday. Now, Xii = 1, as this factor is true.
- Wii is the weight of the second input factor, Xii. In our example, Wii = 3.
- Xiii is the third input factor, It is an occasion for cake. Now, Xiii = 0, as this factor is false.
- Wiii is the weight of the third input factor, Xiii. In our example, Wiii = 6.
- threshold is 4.
We know that the neuron computes the following equation:

For scenario 3, the equation will translate to this:

This gives us the following equation:

5 ≥ 4 is true, so this fires 1, which means I can eat the cake.
From the preceding three scenarios, we saw how a single artificial neuron works. This single unit is also called a perceptron. A perceptron essentially handles binary inputs, computes the sum, and then compares with a threshold to ultimately give a binary output.
To better appreciate how a perceptron works, we can translate our preceding equation into a more generalized form for the sake of explanation.
Let's assume there is just one input factor, for simplicity:

Let's also assume that threshold = b. Our equation was as follows:

It now becomes this:

It can also be written as  , then output 1 else 0.
, then output 1 else 0.
Here, the following applies:
- w is the weight of the input
- b is the threshold and is referred to as the bias
This rule summarizes how a perceptron neuron works.
Just like the mammalian brain, an ANN is made up of many such perceptions that are stacked and layered together. In the next section, we will get an understanding of how these neurons work together within an ANN.
ANNs
Like biological neurons, artificial neurons also do not exist on their own. They exist in a network with other neurons. Basically, the neurons exist by feeding information to each other; the outputs of some neurons are inputs to some other neurons.
In any ANN, the first layer is called the Input Layer. These inputs are real values, such as the factors with weights (w.x) in our previous example. The sum values from the input layer are propagated to each neuron in the next layer. The neurons of that layer do the computation and pass their output to the next layer, and so on:

The layer that receives input from all previous neurons and passes its output to all of the neurons of the next layer is called a Dense layer. As this layer is connected to all of the neurons of the previous and next layer, it is also commonly referred to as a Fully Connected Layer.
The input and computation flow from layer to layer and finally end at the Output Layer, which gives the end estimate of the whole ANN.
The layers in-between the input and the output layers are called the Hidden Layers, as the values of the neurons within these hidden layers are unknown and a complete black box to the practitioner.
As you increase the number of layers, you increase the abstraction of the network, which in turn increases the ability of the network to solve more complex problems. When there are over three hidden layers, then it is referred to as a deepnet.
So, if this was a machine vision task, then the first hidden layer would be looking for edges, the next would look for corners, the next for curves and simple shapes, and so on:

Therefore, the complexity of the problem can determine the number of layers that are required; more layers lead to more abstractions. These layers can be very deep, with 1,000 or more layers, to very shallow, with just about half a dozen layers. Increasing the number of hidden layers does not necessarily give better results as the abstractions may be redundant.
So far, we have seen how artificial neurons can be stacked together to form a neural network. But we have seen that the perceptron neuron takes only binary input and gives only binary output. But in practice, there is a problem in doing things based on the perceptron's idea. This problem is addressed by activation functions.
Activation functions
We now know that an ANN is created by stacking individual computing units called perceptrons. We have also seen how a perceptron works and have summarized it as Output 1, IF  .
.
That is, it either outputs a 1 or a 0 depending on the values of the weight, w, and bias, b.
Let's look at the following diagram to understand why there is a problem with just outputting either a 1 or a 0. The following is a diagram of a simple perceptron with just a single input, x:

For simplicity, let's call  , where the following applies:
, where the following applies:
- w is the weight of the input, x, and b is the bias
- a is the output, which is either 1 or 0
Here, as the value of z changes, at some point, the output, a, changes from 0 to 1. As you can see, the change in output a is sudden and drastic:

What this means is that for some small change,  , we get a dramatic change in the output, a. This is not particularly helpful if the perceptron is part of a network, because if each perceptron has such drastic change, it makes the network unstable and hence the network fails to learn.
, we get a dramatic change in the output, a. This is not particularly helpful if the perceptron is part of a network, because if each perceptron has such drastic change, it makes the network unstable and hence the network fails to learn.
Therefore, to make the network more efficient and stable, we need to slow down the way each perceptron learns. In other words, we need to eliminate this sudden change in output from 0 to 1 to a more gradual change:

This is made possible by activation functions. Activation functions are functions that are applied to a perceptron so that instead of outputting a 0 or a 1, it outputs any value between 0 and 1.
This means that each neuron can learn slower and at a greater level of detail by using smaller changes,  . Activation functions can be looked at as transformation functions that are used to transform binary values in to a sequence of smaller values between a given minimum and maximum.
. Activation functions can be looked at as transformation functions that are used to transform binary values in to a sequence of smaller values between a given minimum and maximum.
There are a number of ways to transform the binary outcomes to a sequence of values, namely the sigmoid function, the tanh function, and the ReLU function. We will have a quick look at each of these activation functions now.
Sigmoid function
The sigmoid function is a function in mathematics that outputs a value between 0 and 1 for any input:

Here,  and
and  .
.
Let's understand sigmoid functions better with the help of some simple code. If you do not have Python installed, no problem: we will use an online alternative for now at https://www.jdoodle.com/python-programming-online. We will go through a complete setup from scratch in Chapter 2, Creating a Real-Estate Price Prediction Mobile App. Right now, let's quickly continue with the online alternative.
Once we have the page at https://www.jdoodle.com/python-programming-online loaded, we can go through the code step by step and understand sigmoid functions:
- First, let's import the math library so that we can use the exponential function:
from math import e
- Next, let's define a function called sigmoid, based on the earlier formula:
def sigmoid ( x ):
return 1 / ( 1 + e **- x )
- Let's take a scenario where our z is very small, -10. Therefore, the function outputs a number that is very small and close to 0:
sigmoid(-10)
4.539786870243442e-05
- If z is very large, such as 10000, then the function will output the maximum possible value, 1:
sigmoid(10000)
1.0
Therefore, the sigmoid function transforms any value, z, to a value between 0 and 1. When the sigmoid activation function is used on a neuron instead of the traditional perceptron algorithm, we get what is called a sigmoid neuron:
Tanh function
Similar to the sigmoid neuron, we can apply an activation function called tanh(z), which transforms any value to a value between -1 and 1.
The neuron that uses this activation function is called a tanh neuron:

ReLU function
Then there is an activation function called the Rectified Linear Unit, ReLU(z), that transforms any value, z, to 0 or a value above 0. In other words, it outputs any value below 0 as 0 and any value above 0 as the value itself:

Just to summarize our understanding so far, the perceptron is the traditional and outdated neuron that is rarely used in real implementations. They are great to get a simplistic understanding of the underlying principle; however, they had the problem of fast learning due to the drastic changes in output values.
We use activation functions to reduce the learning speed and determine finer changes in z or  . Let's sum up these activation functions:
. Let's sum up these activation functions:
- The sigmoid neuron is the neuron that uses the sigmoid activation function to transform the output to a value between 0 and 1.
- The tanh neuron is the neuron that uses the tanh activation function to transform the output to a value between -1 and 1.
- The ReLU neuron is the neuron that uses the ReLU activation function to transform the output to a value of either 0 or any value above 0.
The sigmoid function is used in practice but is slow compared to the tanh and ReLU functions. The tanh and ReLU functions are commonly used activation functions. The ReLU function is also considered state of the art and is usually the first choice of activation function that's used to build ANNs.
Here is a list of commonly used activation functions:

In the projects within this book, we will be primarily using either the sigmoid, tanh, or the ReLU neurons to build our ANN.
Cost functions
To quickly recap, we know how a basic perceptron works and its pitfalls. We then saw how activation functions overcame the perceptron's pitfalls, giving rise to other neuron types that are in use today.
Now, we are going to look at how we can tell when the neurons are wrong. For any type of neuron to learn, it needs to know when it outputs the wrong value and by what margin. The most common way to measure how wrong the neural network is, is to use a cost function.
A cost function quantifies the difference between the output we get from a neuron to an output that we need from that neuron. There are two common types of cost functions that are used: mean squared error and cross entropy.
Mean squared error
The mean squared error (MSE) is also called a quadratic cost function as it uses the squared difference to measure the magnitude of the error:

Here, the following applies:
- a is the output from the ANN
- y is the expected output
- n is the number of samples used
The cost function is pretty straightforward. For example, consider a single neuron with just one sample, (n=1). If the expected output is 2 (y=2) and the neuron outputs 3 (a=3), then the MSE is as follows:



Similarly, if the expected output is 3 (y=3) and the neuron outputs 2 (a=2), then the MSE is as follows:



Therefore, the MSE quantifies the magnitude of the error made by the neuron. One of the issues with MSE is that when the values in the network get large, the learning becomes slow. In other words, when the weights (w) and bias (b) or z get large, the learning becomes very slow. Keep in mind that we are talking about thousands of neurons in an ANN, which is why the learning slows down and eventually stagnates with no further learning.
Cross entropy
Cross entropy is a derivative-based function as it uses the derivative of a specially designed equation, which is given as follows:

Cross entropy allows the network to learn faster when the difference between the expected and actual output is greater. In other words, the bigger the error, the faster it helps the network learn. We will get our heads around this using some simple code.
Like before, for now, you can use an online alternative if you do not have Python already installed, at https://www.jdoodle.com/python-programming-online. We will cover the installation and setup in Chapter 2, Creating a Real-Estate Price Prediction Mobile App. Follow these steps to see how a network learns using cross entropy:
- First, let's import the math library so that we can use the log function:
from numpy import log
- Next, let's define a function called cross_enrtopy, based on the preceding formula:
def cross_entropy(y,a):
return -1 *(y*log(a)+(1-y)*log (1-a))
- For example, consider a single neuron with just one sample, (n=1). Say the expected output is 0 (y=0) and the neuron outputs 0.01 (a=0.01):
cross_entropy(0, 0.01)
The output is as follows:
0.010050335853501451
Since the expected and actual output values are very small, the resultant cost is very small.
Similarly, if the expected and actual output values are very large, then the resultant cost is still small:
cross_entropy(1000,999.99)
The output is as follows:
0.010050335853501451
Similarly, if the expected and actual output values are far apart, then the resultant cost is large:
cross_entropy(0,0.9)
The output is as follows:
2.3025850929940459
Therefore, the larger the difference in expected versus actual output, the faster the learning becomes. Using cross entropy, we can get the error of the network, and at the same time, the magnitude of the weights and bias is irrelevant, helping the network learn faster.
Gradient descent
Up until now, we have covered the different kind of neurons based on the activation functions that are used. We have covered the ways to quantify inaccuracy in the output of a neuron using cost functions. Now, we need a mechanism to take that inaccuracy and remedy it.
The mechanism through which the network can learn to output values closer to the expected or desired output is called gradient descent. Gradient descent is a common approach in machine learning for finding the lowest cost possible.
To understand gradient descent, let's use the single neuron equation we have been using so far:

Here, the following applies:
- x is the input
- w is the weight of the input
- b is the bias of the input
Gradient descent can be represented as follows:

Initially, the neuron starts by assigning random values for w and b. From that point onward, the neuron needs to adjust the values of w and b so that it lowers or decreases the error or cost (cross entropy).
Taking the derivative of the cross entropy (cost function) results in a step-by-step change in w and b in the direction of the lowest cost possible. In other words, gradient descent tries to find the finest line between the network output and expected output.
The weights are adjusted based on a parameter called the learning rate. The learning rate is the value that is adjusted to the weight of the neuron to get an output closer to the expected output.
Keep in mind that here, we have used only a single parameter; this is only to make things easier to comprehend. In reality, there are thousands upon millions of parameters that are taken into consideration to lower the cost.
Backpropagation – a method for neural networks to learn
Great! We have come a long way, from looking at the biological neuron, to the types of neuron, to determining accuracy, and correcting the learning of the neuron. Only one question remains: how can the whole network of neurons learn together?
Backpropagation is an incredibly smart approach to making gradient descent happen throughout the network across all layers. Backpropagation leverages the chain rule from calculus to make it possible to transfer information back and forth through the network:

In principle, the information from the input parameters and weights is propagated through the network to make a guess at the expected output and then the overall inaccuracy is backpropagated through the layers of the network so that the weights can be adjusted and the output can be guessed again.
This single cycle of learning is called a training step or iteration. Each iteration is performed on a batch of the input training samples. The number of samples in a batch is called batch size. When all of the input samples have been through an iteration or training step, then it is called an epoch.
For example, let's say there are 100 training samples and in every iteration or training step, there are 10 samples being used by the network to learn. Then, we can say that the batch size is 10 and it will take 10 iterations to complete a single epoch. Provided each batch has unique samples, that is, if every sample is used by the network at least once, then it is a single epoch.
This back-and-forth propagation of the predicted output and the cost through the network is how the network learns.
We will revisit training step, epoch, learning rate, cross entropy, batch size, and more during our hands-on sections.
Softmax
We have reached our final conceptual topic for this chapter. We've covered types of neurons, cost functions, gradient descent, and finally a mechanism to apply gradient descent across the network, making it possible to learn over repeated iterations.
Previously, we saw the input layer and dense or hidden layers of an ANN:

Softmax is a special kind of neuron that's used in the output layer to describe the probability of the respective output:

To understand the softmax equation and its concepts, we will be using some code. Like before, for now, you can use any online Python editor to follow the code.
First, import the exponential methods from the math library:
from math import exp
For the sake of this example, let's say that this network is designed to classify three possible labels: A, B, and C. Let's say that there are three signals going into the softmax from the previous layers (-1, 1, 5):
a=[-1.0,1.0,5.0]
The explanation is as follows:
- The first signal indicates that the output should be A, but is weak and is represented with a value of -1
- The second signal indicates that the output should be B and is slightly stronger and represented with a value of 1
- The third signal is the strongest, indicating that the output should be C and is represented with a value of 5
These represented values are confidence measures of what the expected output should be.
Now, let's take the numerator of the softmax for the first signal, guessing that the output is A:

Here, M is the output signal strength indicating that the output should be A:
exp(a[0]) # taking the first element of a[-1,1,5] which represents A
0.36787944117144233
Next, there's the numerator of the softmax for the second signal, guessing that the output is B:

Here, M is the output signal strength indicating that the output should be B:
exp(a[0]) # taking the second element of a[-1,1,5] which represents B
2.718281828459045
Finally, there's the numerator of the softmax for the second signal, guessing that the output is C:

Here, M is the output signal strength indicating that the output should be C:
exp(a[2])
# taking the third element of a[-1,1,5] which represents C
148.4131591025766
We can observe that the represented confidence values are always placed above 0 and that the resultant is made exponentially larger.
Now, let's interpret the denominator of the softmax function, which is a sum of the exponential of each signal value:

Let's write some code for softmax function:
sigma = exp ( a [ 0 ]) + exp ( a [ 1 ]) + exp ( a [ 2 ])
sigma
151.49932037220708
Therefore, the probability that the first signal is correct is as follows:
exp(a[0])/sigma
0.0024282580295913376
This is less than a 1% chance that it is A.
Similarly, the probability that the third signal is correct is as follows:
exp(a[2])/sigma
0.9796292071670795
This means there is over a 97% chance that the expected output is indeed C.
Essentially, the softmax accepts a weighted signal that indicates the confidence of some class prediction and outputs a probability score between 0 to 1 for all of those classes.
Great! We have made it through the essential high-level theory that's required to get us hands on with our projects. Next up, we will summarize our understanding of these concepts by exploring the TensorFlow Playground.
TensorFlow Playground
Before we get started with the TensorFlow Playground, let's recap the essential concepts quickly. It will help us appreciate the TensorFlow Playground better.
The inspiration for neural networks is the biological brain, and the smallest unit in the brain is a neuron.
A Perceptron is a neuron based on the idea of the biological neuron. The perceptron basically deals with binary inputs and outputs, making it impractical for actual pragmatic purposes. Also, because of its binary nature, it learns too fast due to the drastic change in output for a small change in input, and so does not provide fine details.
Activation functions were used to negate the issue with perceptrons. This gave rise to other types of neurons that deal with values between ranges of 0 to 1, -1 to 1, and so on, instead of just a 0 or a 1.
ANNs are made up of these neurons stacked in layers. There is an input layer, a dense or fully connected layer, and an output layer.
Cost functions, such as MSE and cross entropy, are ways to measure the magnitude of error in the output of a neuron.
Gradient descent is a mechanism through which a neuron can learn to output values closer to the expected or desired output.
Backpropagation is an incredibly smart approach to making gradient descent happen throughout the network across all layers.
Each back and forth propagation or iteration of the predicted output and the cost through the network is called a training step.
The learning rate is the value that is adjusted to the weight of the neuron at each training step to get an output that's closer to the expected output.
Softmax is a special kind of neuron that accepts a weighted signal indicating the confidence of some class prediction and outputting a probability score between 0 to 1 for all of those classes.
Now, we can proceed to TensorFlow Playground at https://Playground.tensorflow.org. TensorFlow Playground is an online tool to visualize an ANN or deepnet in action, and is an excellent place to reiterate what we have learned conceptually in a visual and intuitive way.
Now, without further ado, let's get on with TensorFlow Playground. Once the page is loaded, you will see a dashboard to create your own neural network for predefined classification problems. Here is a screenshot of the default page and its sections:
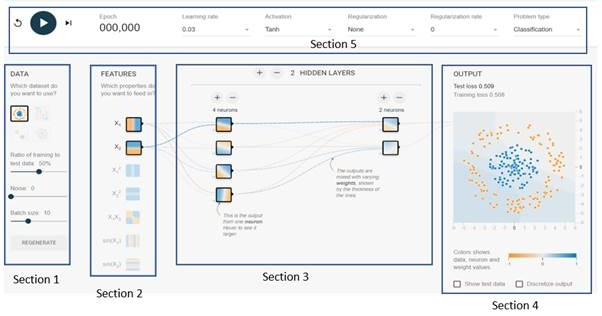
Let's look at each of the sections from this screenshot:
- Section 1: The data section shows choices of the pre-built problems to build and visualize the network. The first problem is chosen, which is basically to distinguish between the blue an orange dots. Below that, there are controls to divide the data into training and testing subsets. There is also a parameter to set the batch size. The Batch size is the number of samples that are taken into the network for learning during each training step.
- Section 2: The features section indicates the number of input parameters. In this case, there are two features chosen as the input features.
- Section 3: The hidden layer section is where we can create hidden layers to increase complexity. There are also controls to increase and decrease the number of neurons within each hidden or dense layer. In this example, there are two hidden layers with four and two neurons, respectively.
- Section 4: The output section is where we can see the loss or the cost graph, along with a visualization of how well the network has learned to separate the red and blue dots.
- Section 5: This section is the control panel for adjusting the tuning parameters of the network. It has a widget to start, pause, and refresh the training of the network. Next to it, there is a counter indicating the number of epochs elapsed. Then there is Learning rate, the constant by which the weights are adjusted. That is followed by the choice of activation function to use within the neurons. Finally, there is an option to indicate the kind of problem to visualize, that is classification, or regression. In this example, we are visualizing a classification task.
- We will ignore the Regularization and Regularization rate for now, as we have not covered these terms in a conceptual manner as of yet. We will visit these terms in later in the book when it is ideal for appreciating its purpose.
We are now ready to start fiddling around with TensorFlow Playground. We will start with the first dataset, with the following settings on the tuning parameters:
- Learning rate = 0.01
- Activation = Tanh
- Regularization = None
- Regularization rate = 0
- Problem type = Classification
- DATA = Circle
- Ratio of training to test data = 50%
- Batch size = 10
- FEATURES = X1 and X2
- Two hidden/dense layers; the first layer with 4 neurons, and the second layer with 2 neurons
Now start training by clicking the play button on the top-left corner of the dashboard. Moving right from the play/pause button, we can see the number of epochs that have elapsed. At about 200 epochs, pause the training and observe the output section:
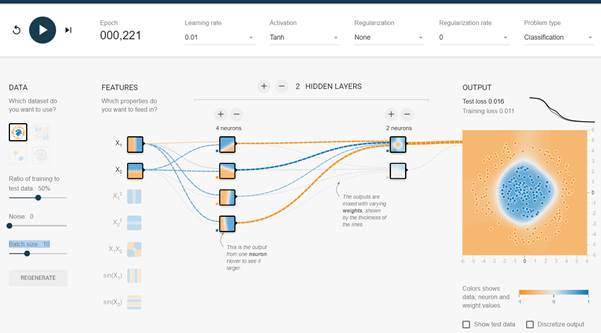
The key observations from the dashboard are as follows:
- We can see the performance graph of the network on the right section of the dashboard. The test and training loss is the cost of the network during testing and training, respectively. As discussed previously, the idea is to minimize cost.
- Below that, you will observe that there is a visualization of how the network has separated or classified the blue dots from the orange ones.
- If we hover the mouse pointer over any of the neurons, we can see what the neuron has learned to separate the blue and orange dots. Having said this, let's take a closer look at both of the neurons from the second layer to see what they have learned about the task.
- When we hover over the first neuron in the second layer, we can see that this neuron has done a good job of learning the task at hand. In comparison, the second neuron in the second layer has learned less about the task.
- That brings us to the dotted lines coming out of the neurons: they are the corresponding weights of the neuron. The blue dotted lines indicate positive weights while the orange dotted ones indicate negative weights. They are commonly called tensors.
Another key observation is that the first neuron in the second layer has a stronger tensor signal coming out of it compared to the second one. This is indicative of the influence this neuron has in the overall task of separating the blue and orange dots, and it is quite apparent when we see what it has learned compared to the overall end results visual.
Now, keeping in mind all the terms we have learned in this chapter, we can play around by changing the parameters and seeing how this affects the overall network. It is even possible to add new layers and neurons.
TensorFlow Playground is an excellent place to reiterate the fundamentals and essential concepts of ANNs.
Summary
So far, we have covered the essential concepts at a high level, enough for us to appreciate the things we are going to be doing practically in this book. Having a conceptual understanding is good enough to get us rolling with building AI models, but it is also handy to have a deeper understanding.
In the next chapter, we will set up our environment for building AI applications and create a small Android and iOS mobile app that can use a model built on Keras and TensorFlow to predict house prices.
Further reading
Here is a list of resources that can be referenced to appreciate and dive deeper into the concepts of AI and deep learning:
- Neural Networks and deep learning, http://neuralnetworksanddeeplearning.com/
- Michael Taylor's Make Your Own Neural Network: An In-depth Visual Introduction For Beginners, https://www.amazon.in/Machine-Learning-Neural-Networks-depth-ebook/dp/B075882XCP
- Tariq Rashid's Make Your Own Neural Network, https://www.amazon.in/Make-Your-Own-Neural-Network-ebook/dp/B01EER4Z4G
- Nick Bostrom's Superintelligence, https://en.wikipedia.org/wiki/Superintelligence:_Paths,_Dangers,_Strategies
- Pedro Domingos's The Master Algorithm, https://en.wikipedia.org/wiki/The_Master_Algorithm
- Deep Learning Book, http://www.deeplearningbook.org/




















 Download code from GitHub
Download code from GitHub




