Linear algebra is one of the essential building blocks of computational mathematics. The objects of linear algebra are vectors and matrices. The package NumPy includes all the necessary tools to manipulate those objects.
The first task is to build matrices and vectors or to alter existing ones by slicing. The other main task is the dot operation, which embodies most linear algebra operations (scalar product, matrix-vector product, and matrix-matrix product). Finally, various methods are available to solve linear problems.
The following topics will be covered in this chapter:
- Overview of the array type
- Mathematical preliminaries
- The array type
- Accessing array entries
- Functions to construct arrays
- Accessing and changing the shape
- Stacking
- Functions acting on arrays
- Linear algebra methods...






















































 is a matrix and
is a matrix and  is a vector, you can solve the linear equation system
is a vector, you can solve the linear equation system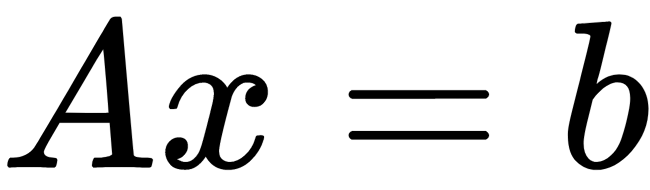

 may just be considered a function from the set of
may just be considered a function from the set of 
 , where we define the set:
, where we define the set:


 . Picking a particular element of an
. Picking a particular element of an matrix may thus be considered a function from
matrix may thus be considered a function from 
 .
. and
and  , defined on the same domain and taking real values. The product
, defined on the same domain and taking real values. The product  of those two functions is defined as the pointwise product, that is,
of those two functions is defined as the pointwise product, that is,

 as follows:
as follows:




 . As a result, its domain is
. As a result, its domain is  . Its shape is defined as the singleton (n,). Similarly, a matrix of size
. Its shape is defined as the singleton (n,). Similarly, a matrix of size 
 . The corresponding shape is simply the pair (m,
. The corresponding shape is simply the pair (m,











 only makes sense if the number of columns of
only makes sense if the number of columns of 






 matrix
matrix :
:






 matrix is the tuple
matrix is the tuple
 is a matrix
is a matrix such that
such that

 . We want to perform a symplectic transformation of a vector with an even number of components, that is, exchange the first half with the second half of the vector with sign change:
. We want to perform a symplectic transformation of a vector with an even number of components, that is, exchange the first half with the second half of the vector with sign change:



 will be a vector of length
will be a vector of length 
 :
:


 matrix and
matrix and
 vectors. We consider the problem to find
vectors. We consider the problem to find 


 are not known simultaneously. In particular, it is quite a common situation that the
are not known simultaneously. In particular, it is quite a common situation that the  th problem has to be solved before
th problem has to be solved before  becomes available, for example in the context of the simplified Newton iteration, see
becomes available, for example in the context of the simplified Newton iteration, see  factorization is a way to organize the classical Gauss elimination method in such a way that the computation is done in two steps:
factorization is a way to organize the classical Gauss elimination method in such a way that the computation is done in two steps:
 and benefits from the more time-consuming factorization step
and benefits from the more time-consuming factorization step
 is the original matrix with its rows permuted, the two systems
is the original matrix with its rows permuted, the two systems  and
and  have the same...
have the same... , with
, with
 matrix and
matrix and  , is called an overdetermined linear system. In general, it has no classical solution and you seek a vector
, is called an overdetermined linear system. In general, it has no classical solution and you seek a vector 

 denotes the Euclidean vector
denotes the Euclidean vector .
.

 orthogonal matrix,
orthogonal matrix,
 orthogonal matrix, and
orthogonal matrix, and  an
an  matrix with the property
matrix with the property  for all
for all . This factorization is called a singular value decomposition (SVD).
. This factorization is called a singular value decomposition (SVD).
 matrix
matrix  . If we assume that
. If we assume that has full rank, then
has full rank, then  is invertible and it can be shown that
is invertible and it can be shown that 
 with
with  being an
being an

 matrix:
matrix:


 (numbered from zero). Given a vector
(numbered from zero). Given a vector  , solve in Python the linear equation system
, solve in Python the linear equation system  . Let the components of
. Let the components of
 . Write a function
. Write a function and
and as input and computes the polynomial:
as input and computes the polynomial:
 as small stars. Try your code with the vectors:
as small stars. Try your code with the vectors:
 in
in
















