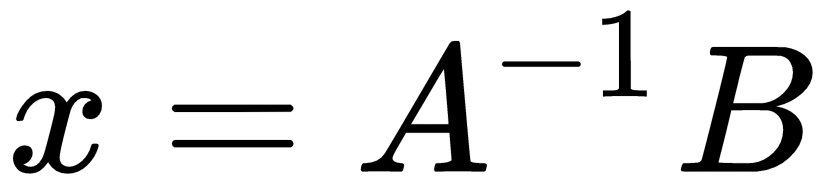One of the major divisions of mathematics is algebra, and linear algebra in particular, focuses on linear equations and mapping linear spaces, namely vector spaces. When we create a linear map between vector spaces, we are actually creating a data structure called a matrix. The main usage of linear algebra is to solve simultaneous linear equations, but it can also be used for approximations for non-linear systems. Imagine a complex model or system that you are trying to understand, think of it as a non-linear model. In such cases, you can reduce the complex, non-linear characteristics of the problem into simultaneous linear equations, and you can solve them with the help of linear algebra.
In computer science, linear algebra is heavily used in machine learning (ML) applications. In ML applications, you deal with high-dimensional arrays, which can easily...























































 is the eigenvector and
is the eigenvector and  denotes the eigenvalue...
denotes the eigenvalue...


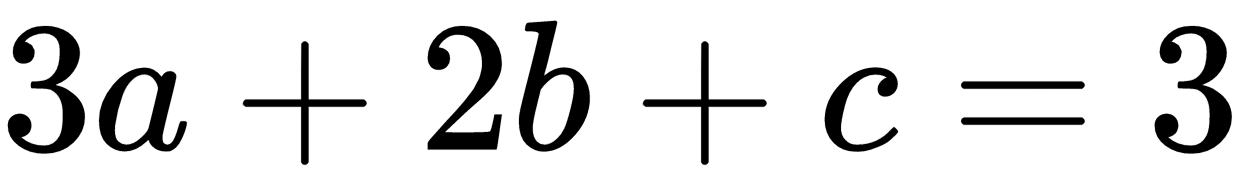
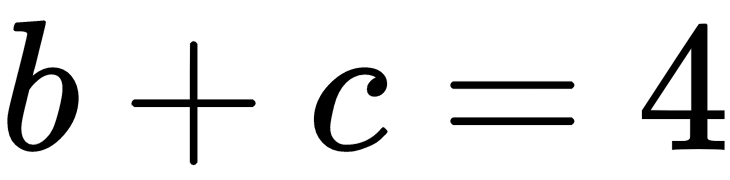
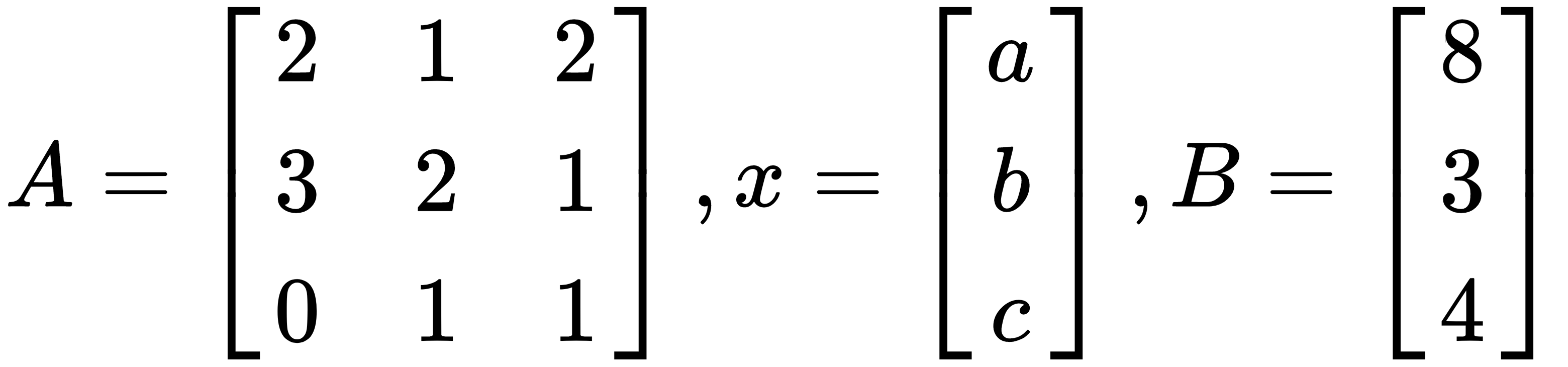
 . We can calculate the solution with a plain vanilla NumPy without using linalg.solve(). After inverting the A matrix, you will multiply with B in order to get results for x. In the following code block, we calculate the dot product for the inverse matrix of A and B in order to calculate
. We can calculate the solution with a plain vanilla NumPy without using linalg.solve(). After inverting the A matrix, you will multiply with B in order to get results for x. In the following code block, we calculate the dot product for the inverse matrix of A and B in order to calculate  :
: