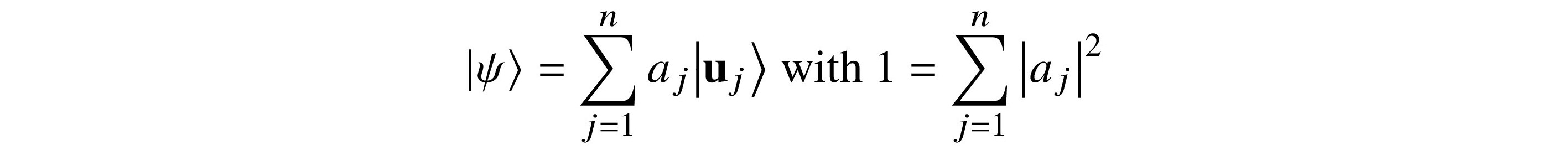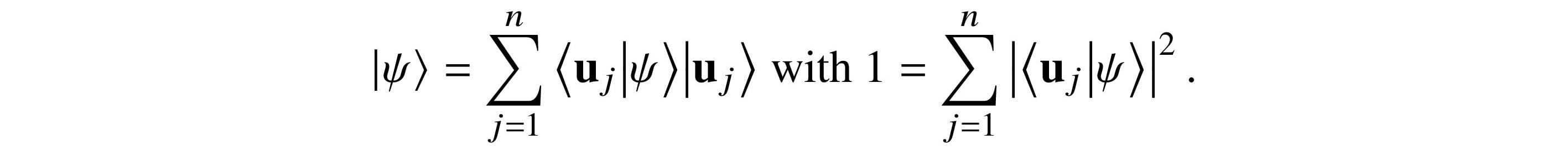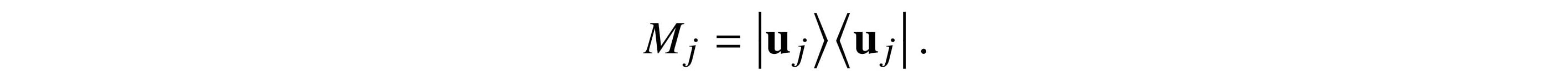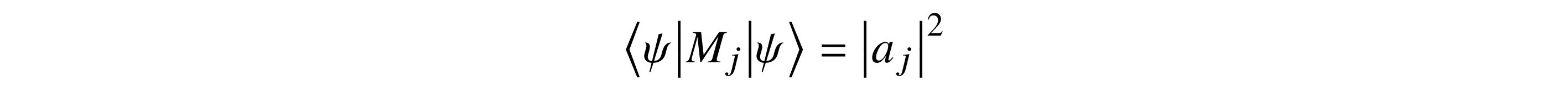Considering NISQ Algorithms

Of all noises, I think music is the least disagreeable.

Samuel Johnson

Noisy Intermediate-Scale Quantum (NISQ) computers have qubits that are not fully fault-tolerant and error-corrected. Decoherence and initialization, gate, and measurement errors make calculations even more unpredictable than normal quantum indeterminacy would indicate. At the time of writing, every available computer is NISQ. NISQ Noisy Intermediate-Scale Quantum era

Do we wait until we have perfect logical qubits to implement the routines in Chapter 10, “From Circuits to Algorithms”? Are there algorithms that use short-depth quantum circuits intermixed with classical methods to approximate solutions to problems that are otherwise exponentially hard? qubit$logical logical qubit

In this chapter, we look at an algorithm for optimization that is an example of a quantum eigensolver that may produce practical results while we wait for full fault tolerance....

Topics covered in this chapter

1. 12.1. Cost functions and optimization
   1. 12.1.1. One-variable functions
   2. 12.1.2. Multivariable functions and gradient descent
2. 12.2. Heuristics
   1. 12.2.1. Graphs
   2. 12.2.2. Max-Cut Problem
   3. 12.2.3. The Knapsack Problem
3. 12.3. Hermitian matrices again
   1. 12.3.1. Hermitian-unitary correspondence
   2. 12.3.2. Pauli strings and sums
4. 12.4. Expectation and the variational principle
5. 12.5. Time evolution
6. 12.6. Parameterized circuits
7. 12.7. The Hamiltonian
8. 12.8. Quantum approximate optimization algorithm (QAOA)
   1. 12.8.1. Encoding the problem
   2. 12.8.2. Mixing things up
   3. 12.8.3. The ansatz and initial state
   4. 12.8.4. The expectation and...

12.1 Cost functions and optimization

Let’s begin with an ad hoc definition of a concept we need when discussing many NISQ algorithms, the cost function, where we defined functions in section 4.1. As you would expect, such a function C computes the cost of something given one or more inputs. We might express the cost in money, work hours, resources consumed, relative health while undergoing a new medical treatment, or any measure of something used or lost. In machine learning, we employ a cost function to measure how close actual data values are to those predicted by a model we construct. optimization function$cost cost$function

In all these examples, we are interested in minimizing the cost function. We want to find when something costs the least money, requires the fewest hours of work or resources, causes the most minor medical trauma or inconvenience, or produces an AI model closest to the training data. This is an optimization problem.

The examples in...

12.2 Heuristics

Is there a difference between an algorithm that provides an exact sequence of steps to follow to solve a problem and a quick-and-dirty solution with shortcuts that may work sometimes? This section discusses the latter, but, for contrast, note that we have seen many examples of exact algorithms: algorithm$heuristic heuristic

• Addition in section 2.5
• Sorting in section 2.8.1
• Searching in section 2.8.2
• Euclid’s algorithm in section 3.4.1
• The Gram-Schmidt orthonormalization process in section 5.7.6
• Quantum teleportation in section 9.3.5
• Amplitude amplification in section 9.6
• Grover’s search algorithm in section 9.7.1
• The Deutsch-Jozsa algorithm in section 9.8
• The Bernstein-Vazirani algorithm in section 9.9
• Simon’s algorithm in section 9.10
• The Quantum Fourier Transform in section 10.1
• Phase estimation in section...

12.3 Hermitian matrices again

Recall that in section 5.4.1, we defined a square n-by-n complex matrix A on a vector space V to be Hermitian if A = A^†: A is equal to its conjugate transpose and is self-adjoint. For the inner product ⟨,⟩,

for all vectors v₁ and v₂ in V. We now need some additional properties of Hermitian matrices for the consideration of NISQ algorithms. matrix$Hermitian matrix$self-adjoint

It follows from the definition of a Hermitian matrix that:

• The diagonal elements of A are real.
• If c is a real number, cA is Hermitian.
• The eigenvalues λ_j of A are real. Some eigenvalues may appear more than once.
• The eigenvectors corresponding to distinct eigenvalues are orthogonal.
• By the Spectral Theorem in section 5.10, we can find {u₁, …, u_n} orthonormal eigenvectors of V with corresponding eigenvalues {λ₁, …, λ_n}. Many proofs regarding...

12.4 Expectation and the variational principle

In section 6.6, we defined the concept of expectation. In section 7.3.4, we further related expectation to observables. Let’s re-express some of those results in terms of eigenvectors u_j and eigenvalues λ_j of a Hermitian matrix A from the last section. expectation observable

Let

be a quantum state. Each a_j = ⟨u_j|ψ⟩. Therefore,

We define

Each M_j is Hermitian and is a projector, meaning that M_j ○ M_j = M_j² = M_j. We have projector

and this is the probability of measuring |u_j⟩. The eigenvectors of M_j are the u_k for 1 ≤ k ≤ n. The eigenvalue of M_j corresponding to u_j is 1. All other eigenvalues are 0.

The M_j are observables since their eigenvectors form a basis for our quantum state vector space by construction.

The expected value, or expectation, ⟨A⟩ of A given the state...

12.5 Time evolution

Another idea we need to understand for NISQ algorithms is time evolution. We begin with some results from single and multivariable calculus, complex analysis, differential equations, and linear algebra. While that is a formidable list of topics, the mathematical objects we manipulate are from Part I of this book. time evolution

Let g be a real-valued function of one real variable t. I chose t because I want you to think of it as the time variable. It is easiest to think of t having values in a continuous portion of R, although it could exclude points where g is not defined. t might take values from a finite set of numbers or a discrete set such as Z. In any case, for two values t₁ and t₂ in the domain of g, with t₁ < t₂, we can consider how g evolves when passing from t₁ to t₂. A common choice is t₁ = 0 and t₂ = 1.

For example, suppose you invest 500 units in some currency in an account that compounds interest continuously at 4% a year. Then...

12.6 Parameterized circuits

The Z gate is fixed in the amount it rotates around the z-axis, while the general R_φ^z gate has the variable parameter φ. When we include such a gate in a circuit, we get a family of circuits that vary with φ. We need such circuits for NISQ algorithms, and we have seen examples of them before.

In section 10.1.3, we developed the circuit for the Quantum Fourier Transform on three qubits and denoted it QFT₃. circuit$parameterized

Figure 12.17: The Quantum Fourier Transform on three qubits

The z-rotations follow a pattern, with angles equal to π divided by powers of 2.

Let’s add a parameter t to the rotation angle, as shown in Figure 12.18. When t = 0, each rotation gate is trivial and is the ID gate. When t = 1, we have QFT₃. We call this circuit with a single parameter U(t).

Figure 12.18: 1-Parameter Quantum Fourier Transform on...

12.7 The Hamiltonian

Time evolution of a quantum system, represented as a sequence of quantum states, occurs via a continuous and additive family of unitary matrices U_t, where we often consider 0 ≤ t ≤ 1. We define each family via Hamiltonian

for some Hermitian matrix H. Other constants that may appear in the numerator are absorbed into H. 189, Section 13.4.2

We call the Hermitian matrix H the Hamiltonian of the quantum system after mathematician and physicist William Rowan Hamilton (Figure 12.20). Being Hermitian, we can write any Hamiltonian as a Pauli sum. Hamilton, William Rowan

Given H in U_t = exp(–iHt), the process of finding an approximate and suitable unitary U_t and related circuit within a given error is known as Hamiltonian simulation. 60 63, Section 2.3 Hamiltonian$simulation simulation$Hamiltonian

Figure 12.20: William Rowan Hamilton (1805–1865)

At this point...

12.8 Quantum approximate optimization algorithm (QAOA)

The quantum approximate optimization algorithm, abbreviated as QAOA, is an example of a variational quantum algorithm. We can use it for combinatorial optimization problems such as the Max-Cut Problem we discussed in section 12.2.2, and we use this problem to illustrate the technique. 18 38 algorithm$QAOA algorithm$quantum approximate optimization quantum$approximate optimization algorithm algorithm$variational QAOA variational$algorithm Max-Cut Problem algorithm$QAOA maximum cut

We begin by constructing the Hamiltonians, unitaries, and circuits we need to perform the optimization.

12.8.1 Encoding the problem

Recall from section 12.2.2 on the Max-Cut Problem that we use the integer vector z with z_k = ±1. z_k = 1 if k is in U, and z_k = –1 if k is in U′. We seek to maximize

We now map this general form with n vertices to Hermitian Pauli strings and a...

12.9 Is NISQ worth it?

The bulk of this book covers algorithms using logical qubits, such as those by Grover (section 9.7.1) and Shor (section 10.7). Since we do not yet have logical qubits, we must make do with physical qubits with their noise and finite (and often short) coherence times. Unlike logical qubit algorithms that may have circuit depths and qubit counts in the thousands or millions, we must make do with a few dozen gates on a few dozen to a few hundred qubits. This situation defines the NISQ era as a prelude to the “Fault-Tolerant Quantum Computing” or “FTQC” era. FTQC logical qubit qubit$logical

Here are some reasons why the development of NISQ algorithms is a good idea:

• NISQ algorithms are a practical way to learn how to characterize quantum hardware systems and improve their control software.
• Improvements in optimizing quantum transpilers for NISQ quantum algorithms will be applicable for implementing...

12.10 Summary

In this chapter, we looked at QAOA as an example of a quantum technique that does not require fault-tolerant, error-corrected qubits. QAOA is an example of a variational quantum eigensolver that uses the variational principle from physics to find solutions to combinatorial optimization problems, such as Max-Cut.

Variational algorithms have potential value because they can use relatively short-depth circuits in conjunction with classical optimization techniques, such as gradient descent. We introduced the concepts of Hamiltonian and ansatz and showed how expectation allows us to compute an upper bound for eigenvalues.

The chapter concluded with a sober look at the perceived versus actual value of NISQ algorithms. Do you think we should bother, or should we focus our efforts on fault-tolerant, error-corrected qubits?