You're reading from A Practical Guide to Quantum Computing Hands-on approach to quantum computing with Qiskit

Product type Paperback

Published in Jul 2025

Last Updated in Aug 2025

Publisher Packt

ISBN-13 9781835885949

Length 512 pages

Edition 1st Edition

Languages

Python

Tools

Azure Quantum

Concepts

Quantum Computing

Authors (2):

Elías F. Combarro Fernández-Combarro Álvarez

Samuel González Castillo

View More author details

Table of Contents (29) Chapters

Preface

1. Part 1 One Qubit to Rule Them All: Working with One Qubit FREE CHAPTER

2. Chapter 1 What Is (and What Is Not) a Quantum Computer

3. Chapter 2 Qubits, Gates, and Measurements

4. Chapter 3 Applications and Protocols with One Qubit

5. Chapter 4 Coding One-Qubit Protocols in Qiskit

6. Part 2 Qubit Meets Qubit: Two Qubits and Entanglement

7. Chapter 5 How to Work with Two Qubits

8. Chapter 6 Applications and Protocols with Two Qubits

9. Chapter 7 Coding Two-Qubit Algorithms in Qiskit

10. Part 3 Working with Many Qubits

11. Chapter 8 How to Work with Many Qubits

12. Chapter 9 The Full Power of Quantum Algorithms

13. Chapter 10 Coding with Many Qubits in Qiskit

14. Part 4 The Stars of the Show: Main Quantum Algorithms

15. Chapter 11 Finding the Period and Factoring Numbers

16. Chapter 12 Searching and Counting with a Quantum Computer

17. Chapter 13 Coding Shor and Grover’s Algorithms in Qiskit

18. Part 5 Ad Astra: The Road to Quantum Utility and Advantage

19. Chapter 14 Quantum Error Correction and Fault Tolerance

20. Chapter 15 Experiments for Quantum Advantage

21. Bibliography

22. Solutions

23. Index

Appendix A Mathematical Tools

1. Appendix B The Bra-Ket Notation and Other Foundational Notions

2. Appendix C Measuring the Complexity of Algorithms

3. Appendix D Installing the Tools

4. Appendix E Production Notes

13.2 Shor’s algorithm

In the previous section, we implemented the inverse quantum Fourier transform, which is central to Shor’s algorithm. However, we still need an additional element if we want to be able to build and run quantum circuits to factor integers: quantum gates for modular multiplication.

Remember that, in order to factor an integer N using Shor’s algorithm, we first choose at random another integer a with no common factors with N. Then, we need to create the following circuit:

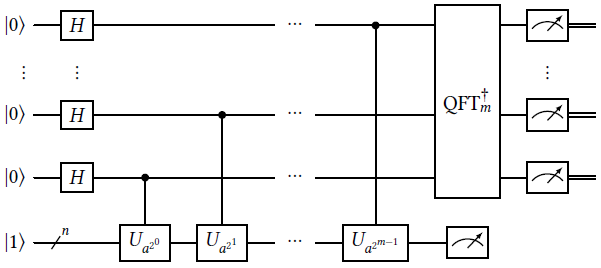
n... |0H⋅Q......|0H⋅|0H⋅|1UU⋅U⋅F⋅⋅aa⋅a⟩⋅T⟩⋅⟩⋅⟩22⋅201m†m−1

Here, the U_a^{2^j} gates implement the operation of multiplying an integer times a^{2^j} and taking the remainder of the division by N. These are the gates that we need to implement now before we can run Shor’s algorithm.

How to implement these quantum gates is a problem that has been extensively studied in the literature, and several very efficient options exist (see, for instance, [72], [73], [74], [75], [76]). However, describing them in detail is beyond the scope of...