Advanced analytics and data science now play a major role in the majority of businesses. It supports organizations in tracking, managing, and gathering performance metrics to enhance organizational decision-making. Business managers can utilize innovative analysis and machine learning to help them decide how to best engage customers, enhance business performance, and increase sales. Data science and analytics can be utilized to create user-centric products and make wise choices. This can be achieved by comparing various product aspects and studying consumer feedback and market trends to develop goods and services that can draw clients and keep them around for an extended period.

This book is intended for everyone who wants to have an introduction to the techniques and methods of data science, advanced analytics, and machine learning for studying business cases that have been impacted by the use of these methods. The cases shown are heavily based on real use cases, with a demonstrated positive impact in various companies of different sectors. So, anyone who might be considering the application of data science in business operations, regardless of whether they are a seasoned business analyst seeking to enhance their list of skills, or a manager looking for methods that can be applied to maximize certain operations, can benefit from the examples discussed in this book.

In this chapter, we will lay down the initial components that will be used throughout this book to manage the data, manipulate it, and visualize it. Specifically, we will discuss the following:

• The use of data science in business and the main differences with roles such as business or data analysts
• The use of statistical programming libraries such as NumPy to apply matrix algebra and statical methods
• Storing the data in pandas, a library for data analysis and manipulation that is widely used in the context of data science
• Visualization with Seaborn and how the different types of charts can be used in different kinds of situations

Next, we will discuss the technical requirements that you will need to be able to follow the examples presented in this chapter.

To be able to follow the steps in this chapter, you will need to meet the following requirements:

• A Jupyter notebook instance running Python 3.7 and above. You can use the Google Colab notebook to run the steps as well if you have a Google Drive account.
• A basic understanding of math and statistical concepts.

Most of the, time the question of what differentiates a data scientist from a business analyst arises, as both roles focus on attaining insight from data. From a certain perspective, it can be considered that data science involves creating forecasts by analyzing the patterns behind the raw data. Business intelligence is backward-looking and discovers the previous and current trends, while data science is forward-looking and forecasts future trends.

Business decision-making strongly relies on data science and advanced analytics because they help managers understand how decisions affect outcomes. As a result, data scientists are increasingly required to integrate common machine learning technologies with knowledge of the underlying causal linkages. These developments have given rise to positions like that of the decision scientist, a technologist who focuses on using technology to support business and decision-making. When compared to a different employment description known as a “data scientist” or “big data scientist,” however, the phrase “decision scientist” becomes truly meaningful.

Most times, there might be confusion between the roles of business analysts, data scientists, and data analysts. Business analysts are more likely to address business problems and suggest solutions, whereas data analysts typically work more directly with the data itself. Both positions are in high demand and are often well paid, but data science is far more engaged in forecasting since it examines the patterns hidden in the raw data.

NumPy is a Python library used for working with arrays. Additionally, it provides functions for working with matrices, the Fourier transform, and the area of linear algebra. Large, multi-dimensional arrays and matrices are now supported by NumPy, along with a wide range of sophisticated mathematical operations that may be performed on these arrays. They use a huge number of sophisticated mathematical functions to process massive multidimensional arrays and matrices, as well as basic scientific computations in machine learning, which makes them highly helpful. It gives the n-dimensional array, a straightforward yet effective data structure. Learning NumPy is the first step on every Python data scientist’s path because it serves as the cornerstone on which nearly all of the toolkit’s capabilities are constructed.

The array, which is a grid of values all of the same type that’s indexed by a tuple of nonnegative integers, is the fundamental building block utilized by NumPy. Similar to how the dimensions of a matrix are defined in algebra, the array’s rank is determined by its number of dimensions. A tuple of numbers indicating the size of the array along each dimension makes up the shape of an array:

import numpy as np
arr = np.array([1, 2, 3, 4, 5])
print(arr)
print(type(arr))

A NumPy array is a container that can house a certain number of elements, all of which must be of the same type, as was previously specified. The majority of data structures employ arrays to carry out their algorithms. Similar to how you can slice a list, you can also slice a NumPy array, but in more than one dimension. Similar to indexing, slicing a NumPy array returns an array that is a view of the original array.

Slicing in Python means taking elements from one given index to another given index. We can select certain elements of an array by slicing the array using [start:end], where we reference the elements of the array from where we can start and where we want to finish. We can also define the step using [start:end:step]:

print('select elements by index:',arr[0])
print('slice elements of the array:',arr[1:5])
print('ending point of the array:',arr[4:])
print('ending point of the array:',arr[:4])

There are three different sorts of indexing techniques: field access, fundamental slicing, and advanced indexing. Basic slicing is the n-dimensional extension of Python’s fundamental slicing notion. By passing start, stop, and step parameters to the built-in slice function, a Python slice object is created. Writing understandable, clear, and succinct code is made possible through slicing. An iterable element is referred to by its position within the iterable when it is “indexed.” Getting a subset of elements from an iterable, depending on their indices, is referred to as “slicing.”

To combine (concatenate) two arrays, we must copy each element in both arrays to result by using the np.concatenate() function:

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
arr = np.concatenate((arr1, arr2))
print(arr)

Arrays can be joined using NumPy stack methods as well. We can combine two 1D arrays along the second axis to stack them on top of one another, a process known as stacking. The stack() method receives a list of arrays that we wish to connect with the axis:

arr = np.stack((arr1, arr2), axis=1)
print(arr)

The axis parameter can be used to reference the axis over which we want to make the concatenation:

arr = np.stack((arr1, arr2), axis=0)
print(arr)

The NumPy mean() function is used to compute the arithmetic mean along the specified axis:

np.mean(arr,axis=1)

You need to use the NumPy mean() function with axis=0 to compute the average by column. To compute the average by row, you need to use axis=1:

np.mean(arr,axis=0)

In the next section, we will introduce pandas, a library for data analysis and manipulation. pandas is one of the most extensively used Python libraries in data science, much like NumPy. It offers high-performance, simple-to-use data analysis tools. In contrast to the multi-dimensional array objects provided by the NumPy library, pandas offers an in-memory 2D table object called a DataFrame.

pandas is an open-source toolkit built on top of NumPy that offers Python programmers high-performance, user-friendly data structures, and data analysis capabilities. It enables quick analysis, data preparation, and cleaning. It performs and produces at a high level.

pandas is a package for data analysis, and because it includes many built-in auxiliary functions, it is typically used for financial time series data, economic data, and any form of tabular data. For scientific computing, NumPy is a quick way to manage huge multidimensional arrays, and it can be used in conjunction with the SciPy and pandas packages.

Constructing a DataFrame from a dictionary is possible by passing this dictionary to the DataFrame constructor:

import pandas as pd
d = {'col1': [1,5,8, 2], 'col2': [3,3,7, 4]}
df = pd.DataFrame(data=d)
df

The pandas groupby function is a powerful and versatile function that allows us to split data into separate groups to perform computations for better analysis:

df = pd.DataFrame({'Animal': ['Dog', 'Dog',
                              'Rat', 'Rat','Rat'],
                   'Max Speed': [380., 370., 24., 26.,25.],
                   'Max Weight': [10., 8.1, .1, .12,.09]})
df

The three steps of “split,” “apply,” and “combine” make it the simplest to recall what a “groupby” performs. Split refers to dividing your data into distinct groups based on a particular column. As an illustration, we can divide our sales data into months:

df.groupby(['Animal']).mean()

pandas’ groupby technique is extremely potent. Using value counts, you can group by one column and count the values of a different column as a function of this column value. We can count the number of activities each person completed using groupby and value counts:

df.value_counts()

We can also aggregate data over the rows using the aggregate() method, which allows you to apply a function or a list of function names to be executed along one of the axes of the DataFrame. The default is 0, which is the index (row) axis. It’s important to note that the agg() method is an alias of the aggregate() method:

df.agg("mean", axis="rows",numeric_only=True)

We can also pass several functions to be used in each of the selected columns:

df.agg({'Max Speed' : ['sum', 'min'], 'Max Weight' : ['mean', 'max']})

The quantile of the values on a given axis is determined via the quantile() method. The row-level axis is the default. The quantile() method calculates the quantile column-wise and returns the mean value for each row when the column axis is specified (axis='columns'). The following line will give us the 10% quantile across the entire DataFrame:

df.quantile(.1)

We can also pass a list of quantiles:

df.quantile([.1, .5])

The pivot() function is used to reshape a given DataFrame structured by supplied index or column values and is one of the different types of functions that we can use to change the data. Data aggregation is not supported by this function; multiple values produce a MultiIndex in the columns:

df = pd.DataFrame(
{'type': ['one', 'one', 'one', 'two', 'two',  'two'],
 'cat': ['A', 'B', 'C', 'A', 'B', 'C'],
'val': [1, 2, 3, 4, 5, 6],
'letter': ['x', 'y', 'z', 'q', 'w', 't']})
df.pivot(index='type', columns='cat', values='val')

Pivot tables are one of pandas’ most powerful features. A pivot table allows us to draw insights from data. pandas provides a similar function called pivot_table(). It is a simple function but can produce a very powerful analysis very quickly.

The next step for us will be to learn how to visualize the data to create proper storytelling and appropriate interpretations.

Seaborn is a Python data visualization library based on Matplotlib. It offers a sophisticated drawing tool for creating eye-catching and educational statistical visuals.

The primary distinction between Seaborn and Matplotlib is how well Seaborn handles pandas DataFrames. Beautiful graphics are provided in Python by using simple sets of functions. When dealing with DataFrames and arrays, Matplotlib performs well. It views axes and figures as objects. There are several stateful plotting APIs in it.

Here, we will start our examples using the “tips” dataset, which contains a mixture of numeric and categorical variables:

import seaborn as sns
import matplotlib.pyplot as plt
tips = sns.load_dataset("tips")
f, ax = plt.subplots(figsize=(12, 6))
sns.scatterplot(data=tips, x="total_bill", y="tip", hue="time")

In the preceding code snippet, we have imported Seaborn and Matplotlib; the latter allows users to control certain aspects of the plots created, such as the figure size, which we defined as a 12 by 6 inches size. This creates the layout in which Seaborn will place the visualization.

We are using the scatterplot() function to create a visualization of points where the X-axis refers to the total_bill variable and the Y-axis refers to the tip variable. Here, we are using the hue parameter to color the different dots according to the time categorical variable, which allows us to plot numerical data with a categorical dimension:

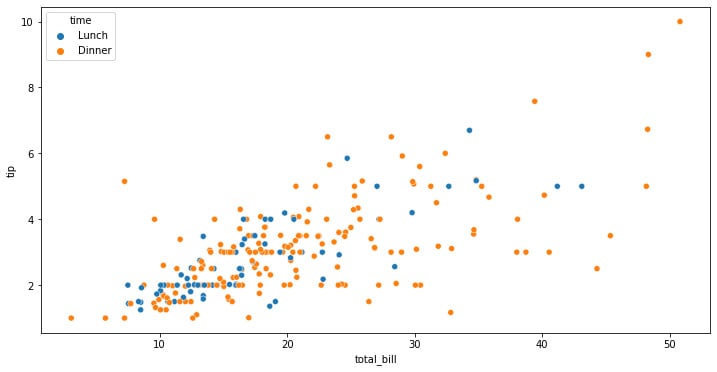
Figure 1.1: Seaborn scatterplot with the color depending on the categorical variable

This generated figure shows the distribution of the data according to the color codes that we have specified, which in our case are the tips that were received, their relationship with the total bill amount, and whether it was during lunch or dinner.

The interpretation that we can make is that there might be a linear relationship between the total amount of the bill and the tip received. But if we look closer, we can see that the highest total bill amounts are placed during dinner, also leading to the highest values in tips.

This information can be really useful in the context of business, but it first needs to be validated with proper hypothesis testing approaches, which can be a t-test to validate these hypotheses, plus a linear regression analysis to conclude that there is a relationship between the total amount and the tip distribution, accounting for the differences in the time in which this occurred. We will look into these analyses in the next chapter.

We can now see how a simple exploration graph can help us construct the hypothesis over which we can base decisions to better improve business products or services.

We can also assign hue and style to different variables that will vary colors and markers independently. This allows us to introduce another categorical dimension in the same graph, which in the case of Seaborn can be used with the style parameter, which will assign different types of markers according to our referenced categorical variable:

f, ax = plt.subplots(figsize=(12, 6))
sns.scatterplot(data=tips, x="total_bill", y="tip", hue="day", style="time")

The preceding code snippet will create a layout that’s 12 x 6 inches and will add information about the time categorical variable, as shown in the following graph:

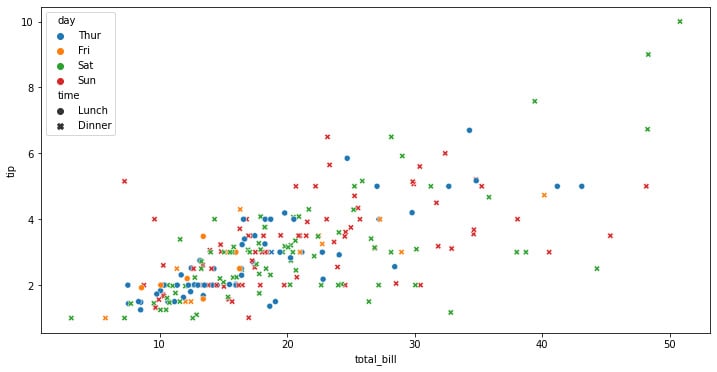
Figure 1.2: Seaborn scatterplot with color and shape depending on the categorical variable

This kind of graph allows us to pack a lot of information into a single plot, which can be beneficial but also can lead to a cluttering of information that can be difficult to digest at once. It is important to always account for the understanding of the information that we want to show, making it easier for the stakeholders to be able to see the relationships at a glance.

Here, it is much more difficult to see any kind of interpretation of the days of the week at first glance. This is because a lot of information is already being shown. These differences that cannot be obtained by simply looking at a graph can be achieved through other kinds of analysis, such as statistical tests, correlations, and causations.

Another way to add more dimensions to the graphics created with Seaborn is to represent numerical variables as the size of the points in the scatterplot. Numerical variables can be assigned to size to apply a semantic mapping to the areas of the points.

We can control the range of marker areas with sizes, and set the legend parameter to full to force every unique value to appear in the legend:

f, ax = plt.subplots(figsize=(12, 6))
sns.scatterplot(
    data=tips, x="total_bill", y="tip", hue="size", 
    size="size", sizes=(20, 200), legend="full"
)

The preceding code snippet creates a scatterplot where the points have a size and color that depends on the size variable. This can be useful to pack another numerical dimension into these kinds of plots:

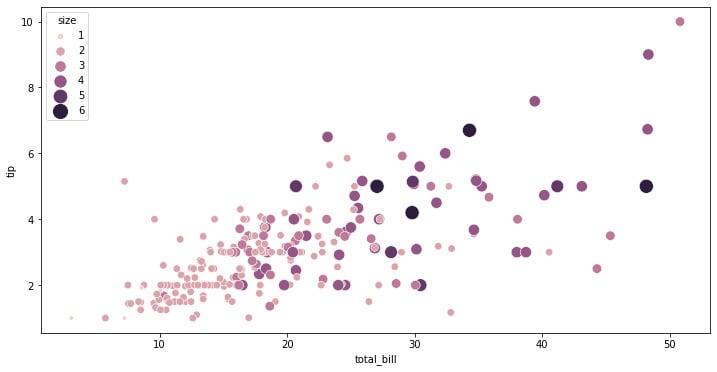
Figure 1.3: Seaborn scatterplot with size depending on a third variable

Another important way to represent data is by looking at time series information. We can use the Seaborn package to display time series data without the need to give the data any special treatment.

In the following example, we are creating a pandas DataFrame with dates, using Matplotlib to create a figure that’s 15 x 8 inches, and then using the Seaborn lineplot function to display the information:

df = pd.DataFrame({"Dates":
['01/01/2019','01/02/2019','01/03/2019','01/04/2019',
'01/05/2019','01/06/2019','01/07/2019','01/08/2019'],
"Count": [727,716,668,710,718,732,694,755]})
plt.figure(figsize = (15,8))
sns.lineplot(x = 'Dates', y = 'Count',data = df)

The preceding example creates a wonderful plot with the dates on the x axis and the count variable on the y axis:

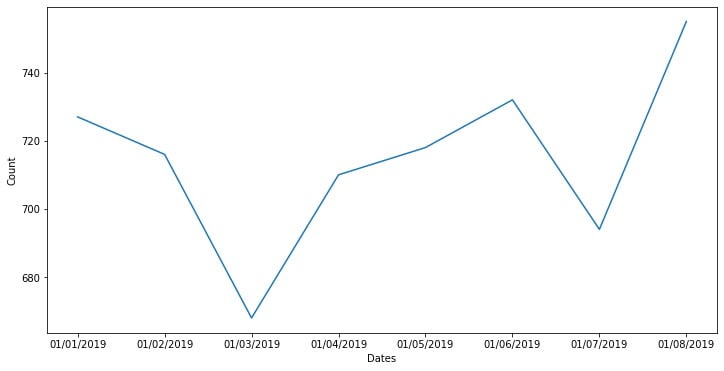
Figure 1.4: Seaborn line plot with a time-based axis

For the following example, we will load a pre-defined dataset from Seaborn known as the FMRI dataset, which contains time series data.

First, we will load an example dataset with long-form data and then plot the responses for different events and regions. To do this, we will create a 15 x 8 inches Matplotlib figure and use the lineplot function to show the information, using the hue parameter to display categorical information about the region, and the style parameter to show categorical information about the type of event:

fmri = sns.load_dataset("fmri")
f, ax = plt.subplots(figsize=(15, 8))
sns.lineplot(x="timepoint", y="signal", hue="region", style="event",data=fmri)

The preceding code snippet creates a display of the information that allows us to study how the variables move through time according to the different categorical aspects of the data:

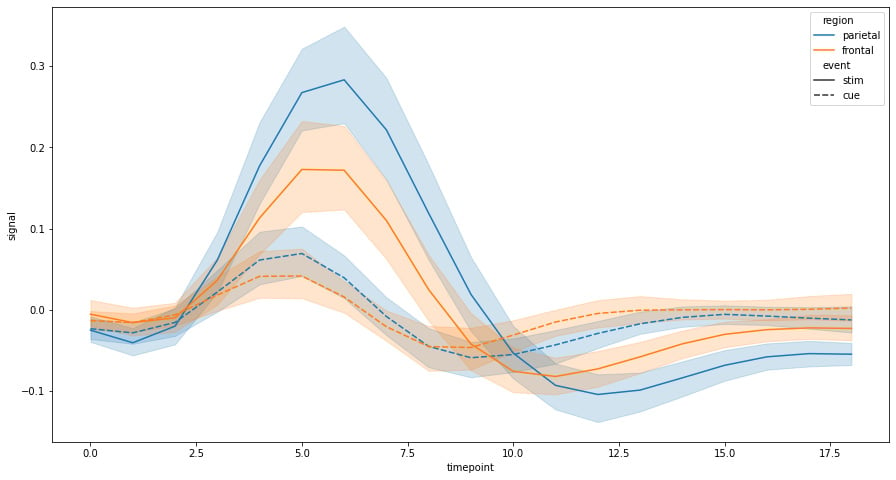
Figure 1.5: Seaborn line plot with confidence intervals

One of the features of the Seaborn lineplot function is that it shows us the confidence intervals of all points within a range of 95% confidence; the solid line represents the main. This way of showing us the information can be really useful when showing time series data that contains multiple data points for each point in time. Trends can be visualized by the mean as well as to give us a sense of the degree of dispersion, which is something that can be important when analyzing behavior patterns.

One of the ways we can visualize data is through bar plots. Seaborn uses the barplot function to create bar plots:

f, ax = plt.subplots(figsize=(12, 6))
ax = sns.barplot(x="day", y="total_bill", data=tips,ci=.9)

The preceding code uses Matplotlib to create a 12 x 6 inches figure where the Seaborn bar plot is created. Here, we will display the days on the x axis and the total bill on the y axis, showing the confidence bars as whiskers above the bars. The preceding code generates the following graph:

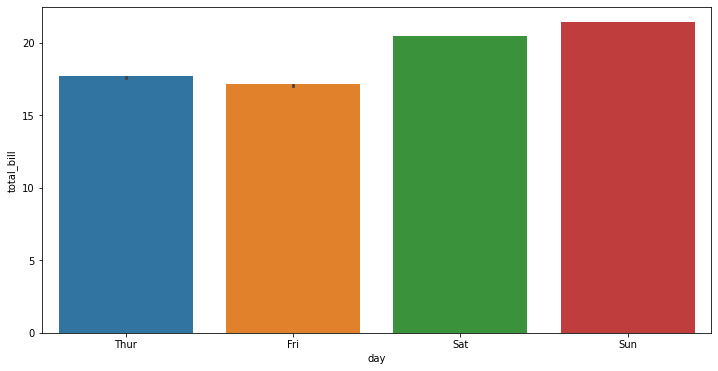
Figure 1.6: Seaborn bar plot

In the preceding graph, we cannot see the whiskers in detail as the data has a very small amount of dispersion. We can see this in better detail by drawing a set of vertical bars while grouping them by two variables:

f, ax = plt.subplots(figsize=(12, 6))
ax = sns.barplot(x="day", y="total_bill", hue="sex", data=tips)

The preceding code snippet creates a bar plot on a 12 x 6-inch Matplotlib figure. The difference is that we use the hue parameter to show gender differences:

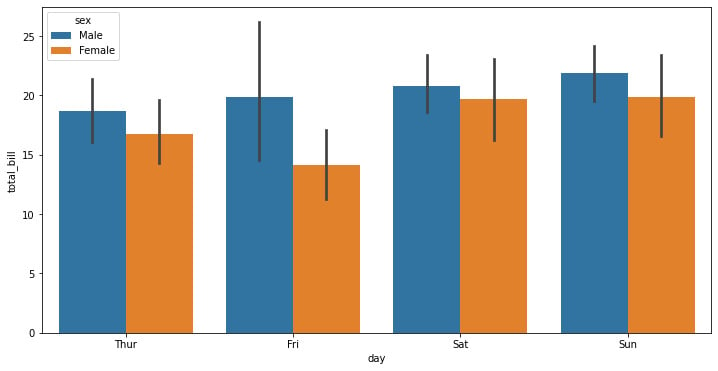
Figure 1.7: Seaborn bar plot with categorical data

One of the conclusions that can be extracted from this graph is that females get to have total bills that are lower than males on average, with Saturday being the only day when there’s a difference between the means, though there’s a much lower basepoint for the dispersion.

We can add another categorical dimension to the visualization using catplot to combine a barplot with a FacetGrid to create multiple plots. This allows us to group within additional categorical variables. Using catplot is safer than using FacetGrid to create multiple graphs as it ensures synchronization of variable order across different facets:

sns.catplot(x="sex", y="total_bill",hue="smoker", col="time",data=tips, kind="bar",height=6, aspect=.7)

The preceding code snippet generates a categorical plot that contains the different bar plots. Note that the size of the graph is controlled using the height and aspect variables instead of via a Matplotlib figure:

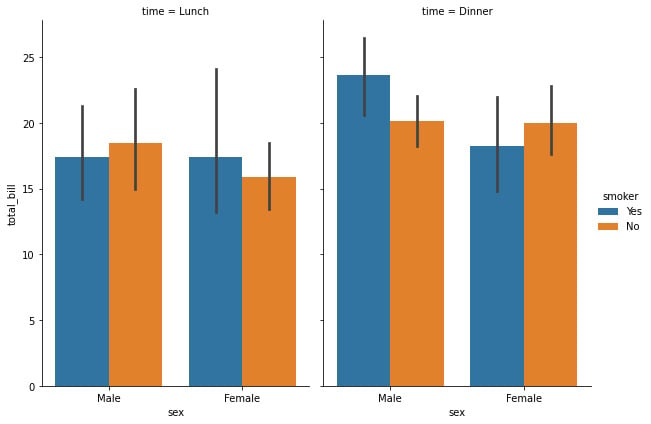
Figure 1.8: Seaborn bar plot with two categorical variables

Here, we can see an interesting trend during lunch, where the mean of the male smokers is lower than the non-smokers, while the female smoker’s mean is higher than those of non-smokers. This tendency is inverted during dinner when there are more male smokers on average than female smokers.

Analyzing trends using histograms is a wonderful tool to be used while analyzing patterns. We can use them with the Searbon hisplot function. Here, we will use the penguins dataset and create a Matplotlib figure that’s 12 x 6 inches:

penguins = sns.load_dataset("penguins")
f, ax = plt.subplots(figsize=(12, 6))
sns.histplot(data=penguins, x="flipper_length_mm", bins=30)

The preceding code creates a histogram of the flipper length grouping data in 30 bins:

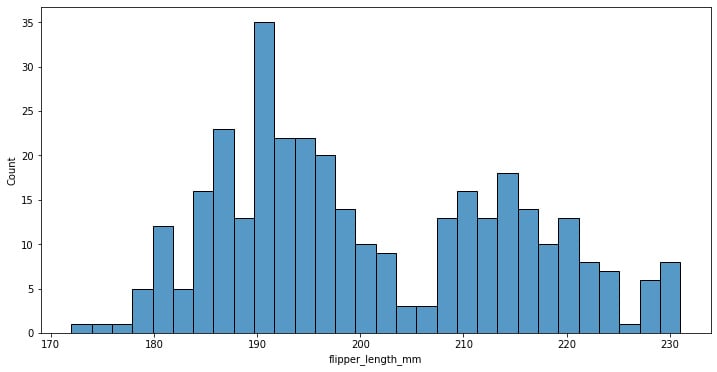
Figure 1.9: Seaborn histogram plot

Here, we can add a kernel density line estimate, which softens the histogram, providing more information about the shape of the data distribution.

The following code adds the kde parameter set to True to show this line:

f, ax = plt.subplots(figsize=(12, 6))
sns.histplot(data=penguins, x="flipper_length_mm", kde=True)

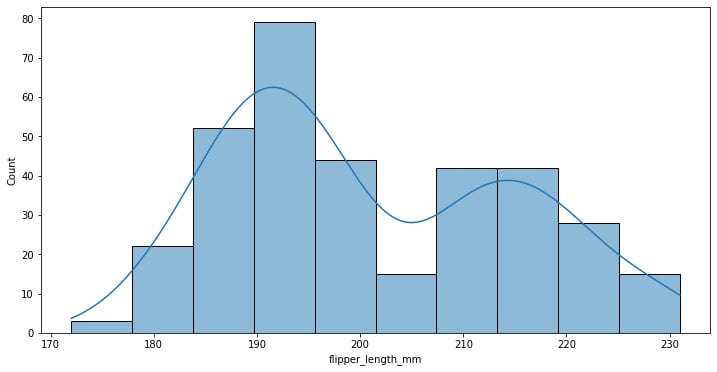
Figure 1.10: Seaborn histogram plot with KDE estimated density

Here, we can see that the data approaches some superimposed standard distribution, which can mean that we are looking at different kinds of data.

We can also add more dimensions to the graph by using the hue parameter on the categorical species variable:

f, ax = plt.subplots(figsize=(12, 6))
sns.histplot(data=penguins, x="flipper_length_mm", hue="species")

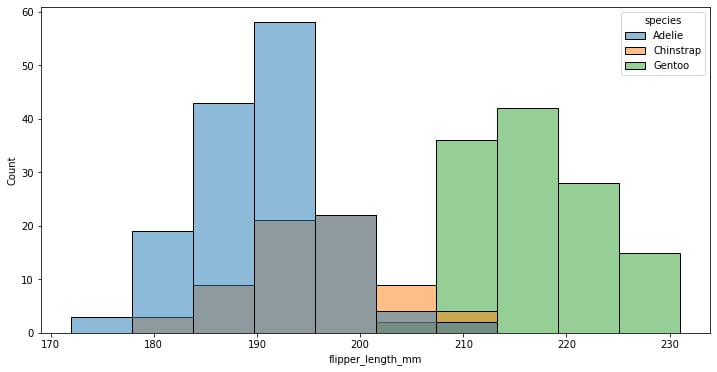
Figure 1.11: Seaborn histogram plot with categorical data

As suspected, we were looking at the superposition of different species of penguins, each of which has a normal distribution, though some of them are more skewed than others.

The pairplot function can be used to plot several paired bivariate distributions in a dataset. The diagonal plots are the univariate plots, and this displays the relationship for the (n, 2) combination of variables in a DataFrame as a matrix of plots. pairplot is used to determine the most distinct clusters or the best combination of features to explain the relationship between two variables. Constructing a linear separation or some simple lines in our dataset also helps to create some basic classification models:

sns.pairplot(penguins,height=3)

The preceding line of code creates a pairplot of the data where each box has a height of 3 inches:

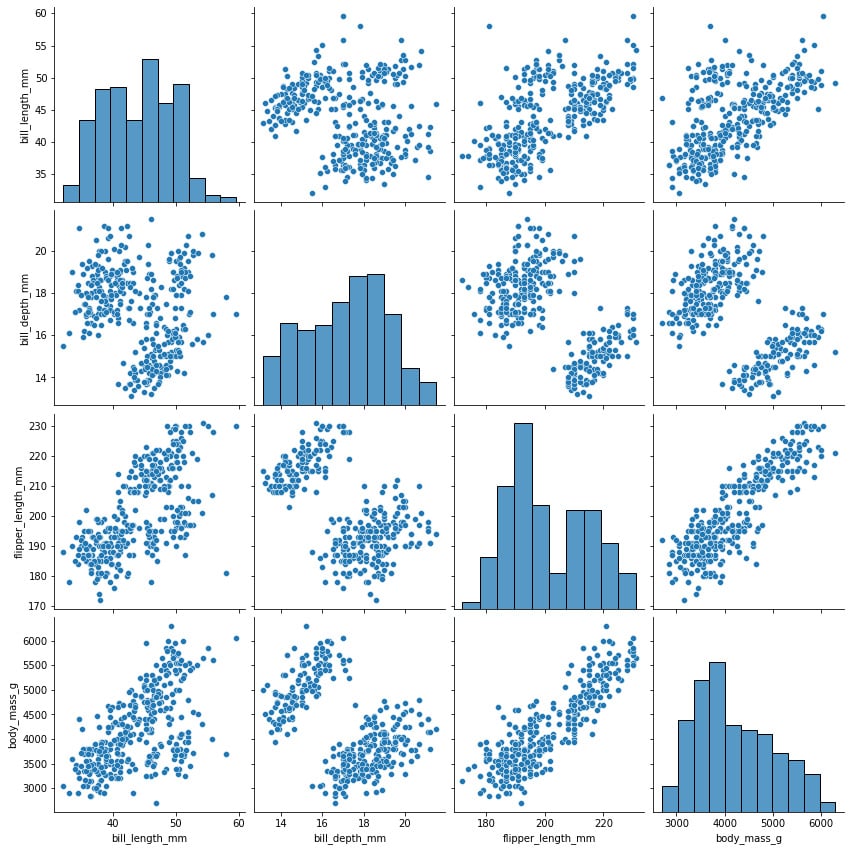
Figure 1.12: Variable relationship and histogram of selected features

The variable names are shown on the matrix’s outer borders, making it easy to comprehend. The density plot for each variable is shown in the boxes along the diagonals. The scatterplot between each variable is displayed in the boxes in the lower left corner.

We can also use the hue parameter to add categorical dimensions to the visualization:

sns.pairplot(penguins, hue="species", diag_kind="hist",height=3)

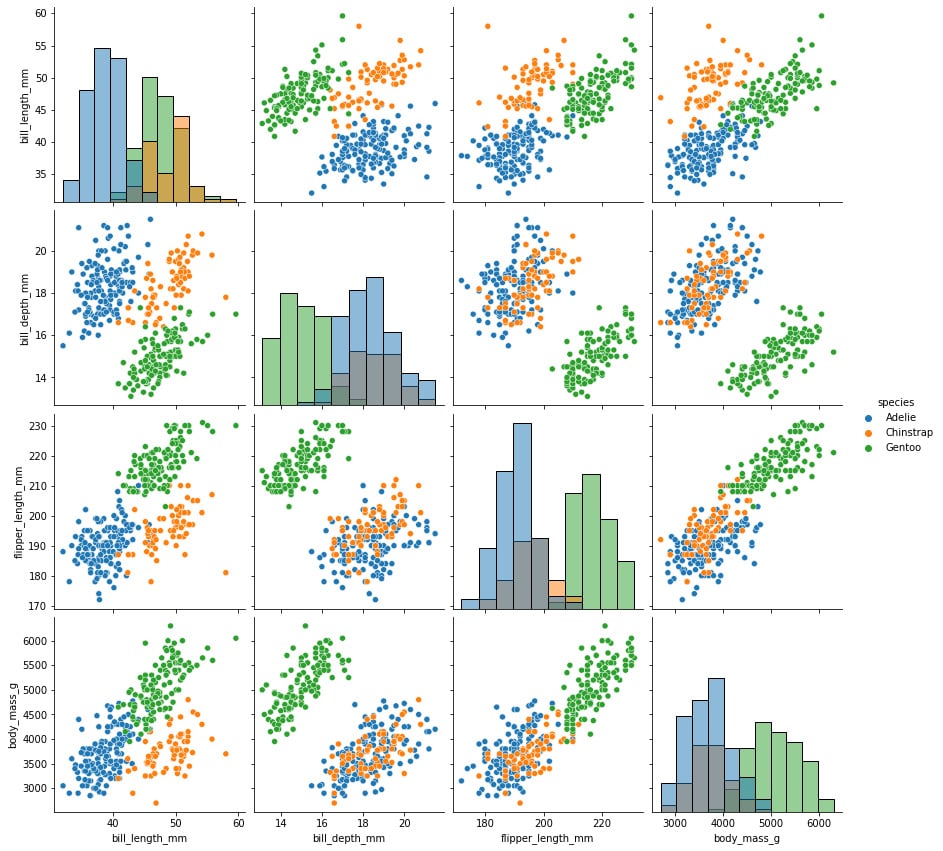
Figure 1.13: Variable relationship and histogram with categorical labels

Although incredibly useful, this graph can be very computationally expensive, which can be solved by looking only at some of the variables instead of the whole dataset.

We can reduce the time required to render the visualization by reducing the number of graphs shown. We can do this by specifying the types of variables we want to show in each axis, as shown in the following block of code:

sns.pairplot(
    penguins,
    x_vars=["bill_length_mm", "bill_depth_mm", 
           "flipper_length_mm"],
    y_vars=["bill_length_mm", "bill_depth_mm"],
    height=3
)

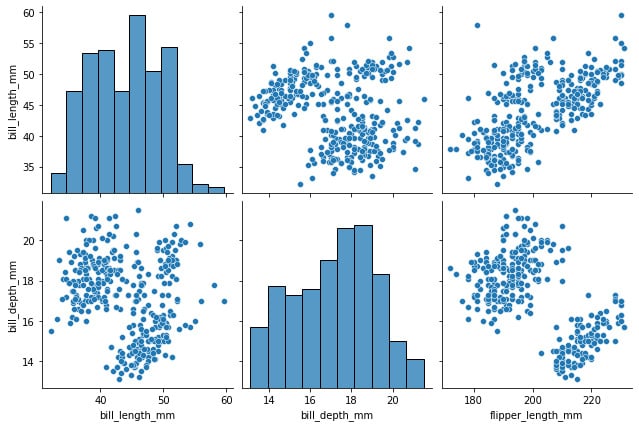
Figure 1.14: Variable relationship and histogram of selected features

A box plot, sometimes referred to as a box-and-whisker plot in descriptive statistics, is a type of chart that is frequently used in explanatory data analysis. Box plots use the data’s quartiles (or percentiles) and averages to visually depict the distribution of numerical data and skewness.

We can use them in Seaborn using the boxplot function, as shown here:

f, ax = plt.subplots(figsize=(12, 6))
ax = sns.boxplot(x="day", y="total_bill", data=tips)

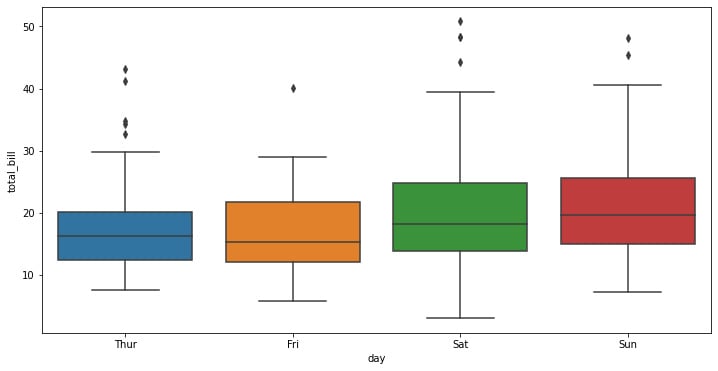
Figure 1.15: Seaborn box plot

The seaborn box plot has a very simple structure. Distributions are represented visually using box plots. When you want to compare data between two groups, they are helpful. A box plot may also be referred to as a box-and-whisker plot. Any box displays the dataset’s quartiles, and the whiskers extend to display the remainder of the distribution.

Here, we can specify a type of categorical variable we might want to show using the hue parameter, as well as specify the palette of colors we want to use from Seaborn’s default options:

f, ax = plt.subplots(figsize=(12, 6))
ax = sns.boxplot(x="day", y="total_bill", hue="smoker",data=tips, palette="Set3")

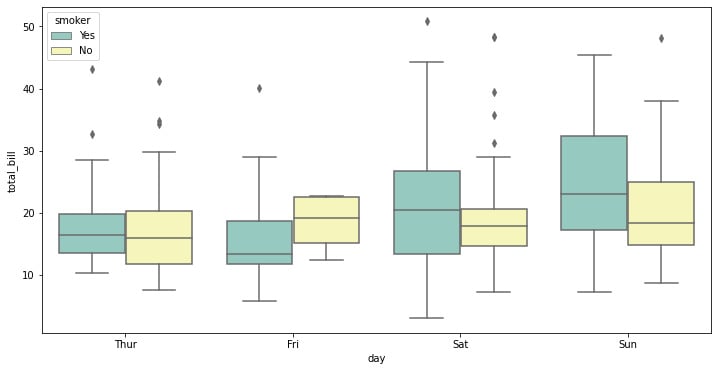
Figure 1.16: Seaborn box plot with categorical data

There is always the question of when you would use a box plot. Box plots are used to display the distributions of numerical data values, particularly when comparing them across various groups. They are designed to give high-level information at a glance and provide details like the symmetry, skew, variance, and outliers of a set of data.

In this chapter, we introduced the initial concepts of how we can store and manipulate data with pandas and NumPy, and how to visualize data patterns using Seaborn. These elements are used not only to explore the data but to be able to create visual narratives that allow us to understand patterns in the data and to be able to communicate simply and practically.

In the next chapter, we will build upon this to understand how machine learning and descriptive statistics can be used to validate hypotheses, study correlations and causations, as well as to make predictive models.