The concepts and techniques of linear algebra are so important and central to the field of quantum computing because almost all of the operations that take place in quantum computing use the language of linear algebra to describe the details and processes that happen within a quantum computer.
Linear algebra deals with the study of vector spaces and matrices. It primarily covers linear mapping and transformations of vectors and matrices. The geometric representation of linear algebra, such as in 2D Cartesian systems, makes it a lot easier to visualize operations happening on vectors and matrices.
In this section, we will cover the essential topics of linear algebra that are relevant to the world of quantum computing. The mathematical terms will be related to their equivalent quantum computing terms so that you can get a full understanding of the technical terms in quantum language. Let's start with the basic building blocks of linear algebra – vectors and vector spaces.
Vectors and vector spaces
In this section, you will develop a fundamental understanding of vectors and vector spaces. You will also learn about the relationship between vectors and the quantum computing world and will come to appreciate the practical nature of the mathematics involved. In quantum computing and quantum mechanics, vector spaces constitute all the possible quantum states, and they obey the rules of addition and multiplication. Vectors and vector spaces also play an important role in fluid mechanics, wave propagation, and oscillators.
Vectors
In the world of classical computation, we represent classical bits as 0, which represents the voltage level being off, and 1, which represents it being on. However, in the world of quantum computing, we use the term qubit, or quantum bit, to represent bits. Quantum bits comprise a two-level quantum system that forms the basic units of information in quantum computation, and they derive their properties from quantum mechanics. You may wonder why I am discussing qubits in the vectors section; this is because qubits can be represented as vectors!
Vectors are just collections or lists of numbers, and in a more geometric sense, they represent direction along with magnitude. Mathematicians refer to these as vectors, whereas quantum physicists and computer scientists call them qubits. I will use the term qubits instead of vectors. The notation to represent qubits is known as the bra-ket notation or Dirac notation and uses angle brackets, <>, and vertical bars, |, to represent the qubits. The paper by Dirac titled A new notation for quantum mechanics explains the bra-ket notation in more detail and can be found in the Further reading section. The basic qubits used most frequently in quantum computing are column vectors (2D).
The 0 qubit can be written as  and 1 can be written as
and 1 can be written as  ; these are called ket 0 and ket 1, respectively. Qubits are quantum states, and a general quantum state can be denoted by
; these are called ket 0 and ket 1, respectively. Qubits are quantum states, and a general quantum state can be denoted by  .
.
We can see a ket representation of qubits as follows:
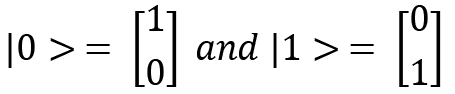
The bra notation, which is the transpose of ket, is given as follows:
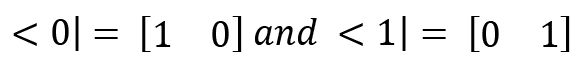
The important properties of the bra-ket notation is as follows:
- Every ket qubit will have a bra qubit.
- Constant multiple property – for a constant multiple c,
 , and
, and  .
.
Vector spaces
A vector space is a collection of vectors where two essential operations can take place, namely, vector addition and scalar multiplication. In quantum computing, you deal with complex vector spaces,  , called Hilbert spaces, which means that vectors can consist of complex numbers, and all the rules of complex numbers can be applied in the calculations whenever we are carrying out operations and calculations with vectors and matrices. Hilbert spaces are usually denoted by the letter H. We will see this more in the next section.
, called Hilbert spaces, which means that vectors can consist of complex numbers, and all the rules of complex numbers can be applied in the calculations whenever we are carrying out operations and calculations with vectors and matrices. Hilbert spaces are usually denoted by the letter H. We will see this more in the next section.
Vector addition can be performed in the following way:
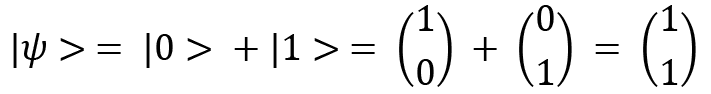
Here, the corresponding elements of the vectors are added together. This can be easily extended to  dimensions as well, where
dimensions as well, where  corresponding elements are added. The quantum state
corresponding elements are added. The quantum state  formed previously is also known as a superposition of quantum states, which means that not only can quantum states be present at
formed previously is also known as a superposition of quantum states, which means that not only can quantum states be present at  or
or  , but they can also be present in the superposition of
, but they can also be present in the superposition of  and
and  . This is a very important property in quantum computation. Superposition states are linear combinations of other quantum states.
. This is a very important property in quantum computation. Superposition states are linear combinations of other quantum states.
According to quantum mechanics, quantum states always need to be normalized because the probabilistic description of wave functions in quantum mechanics means that all the probabilities add to 1, so normalizing the state  will give us
will give us  , which is the proper definition of the state
, which is the proper definition of the state  . The modulus squared of the coefficients of the quantum states gives us the probability of finding that particular state. As an example,
. The modulus squared of the coefficients of the quantum states gives us the probability of finding that particular state. As an example,  is the respective probabilities of finding
is the respective probabilities of finding  and
and  in the preceding case.
in the preceding case.
Scalar multiplication in vector spaces happens as follows:
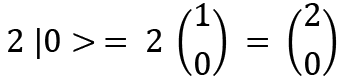
Here the scalar, which can be a real or complex number, is being multiplied by each of the elements present in the vector.
Whenever a vector can be written as a linear combination of other vectors, those vectors are known as linearly dependent vectors. Therefore, the linear independence of vectors implies that vectors cannot be written as a combination of other vectors. For example, the vectors  and
and  are linearly independent, but
are linearly independent, but  is linearly dependent because
is linearly dependent because  can be written as
can be written as  . The vectors
. The vectors  and
and  form the basis vectors and are the most common computational basis used in quantum computation. Similarly, in terms of Cartesian coordinates, the vectors (1, 0) and (0, 1) form the basis vectors for the Cartesian plane.
form the basis vectors and are the most common computational basis used in quantum computation. Similarly, in terms of Cartesian coordinates, the vectors (1, 0) and (0, 1) form the basis vectors for the Cartesian plane.
Vectors and vector spaces are very important concepts and will be used frequently throughout the book. We will now describe some operations that are important for vectors.
Inner products and norms
Inner products is a useful concept for the comparison of closeness between two vectors or quantum states, which is frequently carried out in quantum computing. In this section, you will become familiar with the calculation of inner products and the norms of quantum states. Inner products are useful for identifying the distinguishability of two different quantum states, and this property can be used for clustering. Norms are useful for describing the stretch or range of a particular quantum state in the vector space.
Inner products
The most important difference between an inner product and a dot product is the space and the mapping process. For the dot product, you will be familiar with the fact that the process takes two vectors from the Euclidean space and operates on them to provide us with a real number. In the case of inner products, the two vectors are taken from the  space and the operations map it to a complex number. Inner products measure the closeness between two vectors. The notation <a|b> defines an inner product between two quantum states or two vectors.
space and the operations map it to a complex number. Inner products measure the closeness between two vectors. The notation <a|b> defines an inner product between two quantum states or two vectors.
For calculating, we have  , where
, where  is the transpose of vector a. If
is the transpose of vector a. If  , then the vectors are known as orthogonal vectors. Since the output of the inner product is complex,
, then the vectors are known as orthogonal vectors. Since the output of the inner product is complex,  holds true.
holds true.
Let's solve an example to see the calculation of inner products:
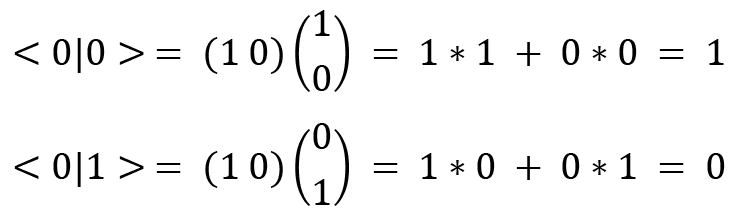
Similarly, you can verify that  and
and  Since
Since  , it shows that
, it shows that  and
and  are orthogonal, but
are orthogonal, but  , which shows that they are normalized. This means that
, which shows that they are normalized. This means that  and
and  are orthonormal!
are orthonormal!
For the calculation of the inner product whenever the elements are complex, the Hermitian conjugate of the vector is necessary to compute. To calculate the Hermitian conjugate, we take the complex conjugate of the elements of the vector and write it in a row vector form. For the computation of inner products, we then multiply the Hermitian conjugate by the column vector. The Hermitian conjugate is denoted by  .
.
Norms
The norm of a vector gives us the length of that vector. This is a real number and is denoted as follows:
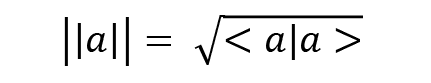
The notion of the length of a vector is also known as the magnitude of the vector, which was mentioned at the beginning of the section on vectors. These operations are important for understanding various quantum algorithms in later chapters.
With inner products, norms, and vector spaces defined, let's now look at a few properties of Hilbert spaces, which are where all quantum computations happen.
Properties of Hilbert spaces
Let's look at some important properties of Hilbert spaces very briefly. You can try solving the proofs of these properties for yourself as a nice exercise:
- A Hilbert space is a linear vector space satisfying the inner product condition –
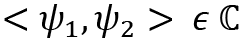
- Hilbert spaces satisfy conjugate symmetry:
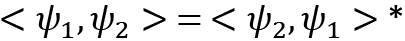
- Hilbert spaces satisfy positive definiteness:
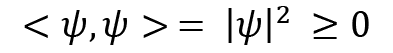
- Hilbert spaces are separable, so they contain a countable dense subset.
- Hilbert spaces satisfy that they are linear with respect to the first vector:
 where
where  are scalars.
are scalars.
- Hilbert spaces satisfy that they are anti-linear with respect to the second vector:
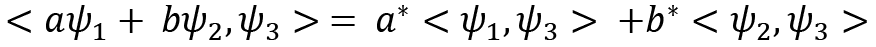
We have discussed the various characteristics of and operations for vectors. Now we will dive into matrices and their operations while describing their relevance to quantum computing.
Matrices and their operations
Matrices are a significant part of quantum computing and their importance can't be emphasized enough. The fundamental concept behind matrices is that they connect theoretical quantum computing with practical quantum computing because they are easily implemented on computers for calculations. In this section, you will learn about matrices and their operations.
A matrix is an array of numbers that are arranged in a tabular format, that is, in the form of rows and columns. Primarily, matrices represent linear transformations in a vector space, making them essentially a process of linear mappings between vector spaces. For example, a rotation matrix is a rectangular array of elements arranged in order to rotate a vector in a 2D or 3D space. From this, you should begin to grasp the idea that whenever a matrix acts on an object, it will create some effect, and the effect is usually in the form of the transformation of functions or spaces. So, matrices can be called operators in the language of quantum computation, or in other words, operators can be represented using matrices.
The general form of a matrix is as follows:

Here  represents the element at the
represents the element at the  row and the
row and the  column. When
column. When  , if the rows and the columns equal each other, then that matrix is known as a square matrix.
, if the rows and the columns equal each other, then that matrix is known as a square matrix.
Since we are now familiar with the matrix notation, let's dive into some basic operations that are performed on matrices for simple calculations. Along the way, we will keep on seeing other forms of matrices that are important to the field of quantum computing.
Transpose of a matrix
We get the transpose of a matrix when we interchange the rows with the columns or the columns with the rows. For example, we can define a matrix A and calculate its transpose as follows:
 . The transpose of A is given as
. The transpose of A is given as  , where T is the transpose. It can be observed that by taking the transpose of matrix A, the diagonal entries –
, where T is the transpose. It can be observed that by taking the transpose of matrix A, the diagonal entries –  – remain unchanged for
– remain unchanged for  . If
. If  , then the matrix is a symmetric matrix. Now you can observe that symmetric matrices or operators are useful because they are able to represent the scaling of different axes, which can be the computational basis for our quantum computation. It is worth observing that
, then the matrix is a symmetric matrix. Now you can observe that symmetric matrices or operators are useful because they are able to represent the scaling of different axes, which can be the computational basis for our quantum computation. It is worth observing that  , which you can verify for yourself. For these reasons, the transpose of a matrix is an important concept to study in quantum computing.
, which you can verify for yourself. For these reasons, the transpose of a matrix is an important concept to study in quantum computing.
Another important property to note here is that symmetric matrices represent the scaling of the computational basis, and asymmetric matrices represent the level of rotation of the computational basis. The rotation and scaling are the fundamental transformations that a matrix can represent.
If a matrix has complex entries such as  , then we always do a conjugate transpose or adjoint of such matrices, which is denoted by
, then we always do a conjugate transpose or adjoint of such matrices, which is denoted by  . We can perform the transpose of
. We can perform the transpose of  first and then do the conjugation, or vice versa:
first and then do the conjugation, or vice versa:
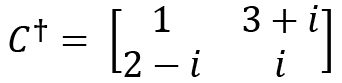
Just as we saw with the definition of a symmetric matrix, if  , that is, the matrix is equal to its adjoint, then it is known as a Hermitian matrix.
, that is, the matrix is equal to its adjoint, then it is known as a Hermitian matrix.
Let's see how we can perform basic arithmetic operations on matrices such as addition and multiplication. Let's start with addition.
Matrix addition
Now, let's see how we can add two matrices. Let's define matrices A and B. Matrix addition is defined only for square matrices. We will look at a general case and then see an example:
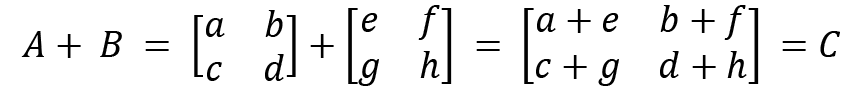
Our example for illustrating the addition of matrices is as follows:
 and B
and B  , then
, then 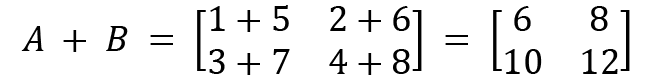
It can be observed that the corresponding elements are added together in matrix addition. The same method can be followed for matrix subtraction as well.
Let's see the properties of matrix addition. For A, B, and C matrices with size m x n, we have the following:
- Commutative:
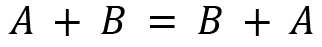
- Associative:
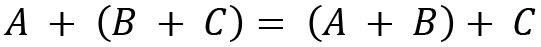
- Additive identity:
 , where O is a unique m x n matrix that, when added to A, gives back A
, where O is a unique m x n matrix that, when added to A, gives back A
- Additive inverse:
 , where
, where 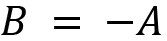
- Transpose property:
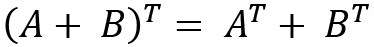
Next, we will look at matrix multiplication.
Matrix multiplication
Let's look at the matrix multiplication process, which will later help us to understand multiple quantum gates applied to qubits in Chapter 2, Quantum Bits, Quantum Measurements, and Quantum Logic Gates. This is defined when the number of columns of the first matrix is equal to the number of rows of the second matrix. Let's take an example of a general case for matrix multiplication:
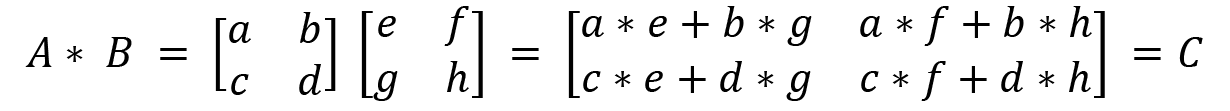
We take this example and multiply A and B together as shown here:
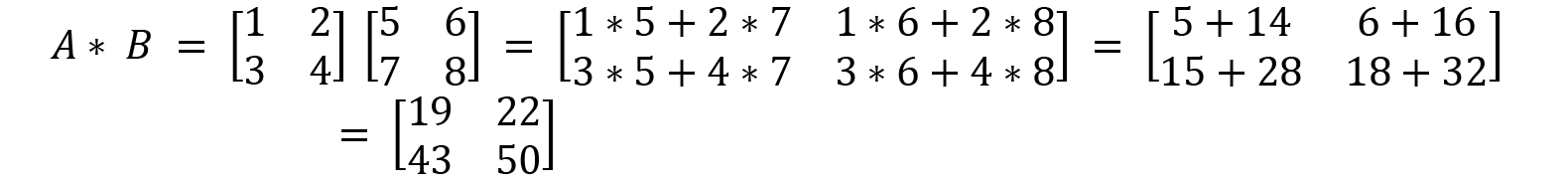
Now, if we define an operator  and make it operate on the qubit
and make it operate on the qubit  , which is like
, which is like  , we can get
, we can get  . We see that
. We see that  remains unchanged by the operation of K. But if you apply
remains unchanged by the operation of K. But if you apply  , then you will get
, then you will get  and you can verify it yourself! This means that the operator K changes the sign of the qubit only when it is in the
and you can verify it yourself! This means that the operator K changes the sign of the qubit only when it is in the  state.
state.
It is useful to remember that  , and similarly, for complex matrices,
, and similarly, for complex matrices,  . It will be a good exercise for you to prove that matrix multiplication is not commutative, which means that for any two matrices
. It will be a good exercise for you to prove that matrix multiplication is not commutative, which means that for any two matrices  .
.
Let's see the properties of matrix multiplication. For A, B, and C matrices with size m x n, we have the following:
- Associative:
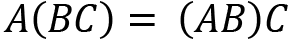
- Distributive:
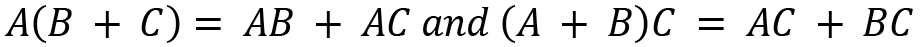
- Multiplicative identity:
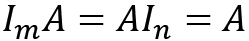
For two scalars c and d, a few properties on scalar multiplication are provided as follows:
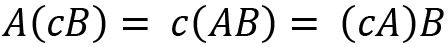
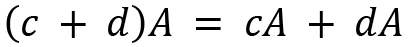
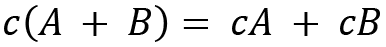
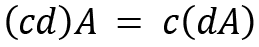
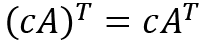
We have now discussed some basic arithmetic operations on matrices. Now let's see how we can calculate the inverse of a matrix.
Inverse of a matrix
The inverse of a matrix represents the undoing of a transformation that has been done by a matrix. So, if the operator K transforms the vector space into some other space, then the inverse of K, denoted as  , can be used to bring back the original vector space.
, can be used to bring back the original vector space.
Let's see the calculation of an inverse of a 2x2 matrix. For a 2x2 matrix, the inverse is defined as follows:  then
then  .
.
If we take  , then its inverse can be calculated as shown:
, then its inverse can be calculated as shown:
 .
.
For an operator K, if  , which means
, which means  , then the operator is known as a unitary operator. I is the identity matrix whose diagonal entries are 1 and the rest are 0. The concept of a unitary operator and transformation are important because according to the postulate of quantum mechanics, time evolution in a quantum system is unitary. This means that these operators preserve the probabilities, and in a more mathematical sense, they preserve the length and angles of the vectors (quantum states). It is worth to note that eigenvalues of a unitary matrix is of a unit modulus.
, then the operator is known as a unitary operator. I is the identity matrix whose diagonal entries are 1 and the rest are 0. The concept of a unitary operator and transformation are important because according to the postulate of quantum mechanics, time evolution in a quantum system is unitary. This means that these operators preserve the probabilities, and in a more mathematical sense, they preserve the length and angles of the vectors (quantum states). It is worth to note that eigenvalues of a unitary matrix is of a unit modulus.
Most of the time, a unitary matrix is denoted by U.
Some interesting properties of unitary matrices are as follows:
- For any two complex vectors
 , the unitary preserves their inner product, so
, the unitary preserves their inner product, so  .
.
- Since U commutes with its conjugate transpose (
 ), it is called a normal matrix.
), it is called a normal matrix.
- The columns of U form an orthonormal basis of
 .
.
- The rows of U form an orthonormal basis of
 .
.
- U is an invertible matrix with the property
 .
.
- The eigenvectors of a unitary matrix are orthogonal.
Next, we will discuss the determinant and trace of a matrix and show how they can be calculated.
The determinant and trace of a matrix
The determinant represents the volume of an n-dimensional parallelepiped formed by the columns of any matrix or an operator. The determinant is a function that takes a square matrix as an input gives a single number as an output. It tells us the linear transformation change for area or volume. For a 2x2 matrix, the determinant is calculated as follows:
 then
then 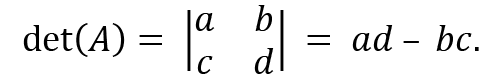
For a 3x3 matrix, the determinant is calculated like this:
 then
then 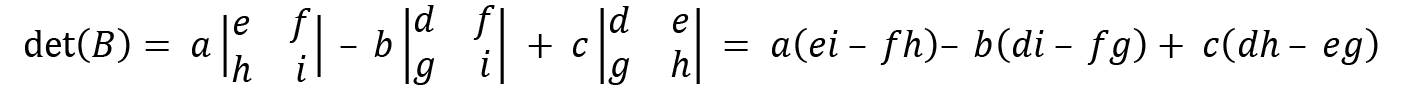
It is worth pointing out that the determinant of a unitary matrix is 1, meaning  . As an exercise, prove that the matrix
. As an exercise, prove that the matrix  is a unitary matrix with a determinant of 1.
is a unitary matrix with a determinant of 1.
The trace of a matrix or operator is defined as the sum of all the diagonal elements. This is given as follows:
If 
 , then
, then 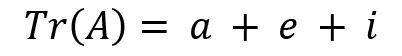
An interesting property to note is that the trace of a matrix also represents the sum of the eigenvalues of the matrix and is a linear operation.
Let's now dive into the expectation value of an operator and its usefulness.
The expectation value (mean value) of an operator
Suppose we prepare a quantum state  many times and we also measure an operator K each time when we prepare that state. This means we now have a lot of measurements with us, so it is natural for us to determine the cumulative effect of the measurement results. This can be done by taking the expected value of the operator K. This is given as follows:
many times and we also measure an operator K each time when we prepare that state. This means we now have a lot of measurements with us, so it is natural for us to determine the cumulative effect of the measurement results. This can be done by taking the expected value of the operator K. This is given as follows:
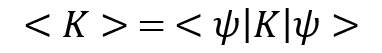
So, the expected value is the average of all the measurement results, which are weighted by the likelihood values of the measurement occurring.
Now that we've learned about the various operations that can be performed on operators, let's learn about some important calculations that are performed on operators: eigenvalues and eigenvectors.
The eigenvalues and eigenvectors of an operator
Eigenvalues and eigenvectors are among the most important topics covered in linear algebra literature as they have a lot of significant applications in various fields. Apart from quantum computing, eigenvalues and eigenvectors find applications in machine learning (for instance, in dimensionality reduction, image compression, and signal processing), communication systems design, designing bridges in civil engineering, Google's Page Rank algorithm, and more.
Conceptually, we search for those vectors that do not change directions under a linear transformation but whose magnitude can change. This is essentially the concept of eigenvectors and eigenvalues. Just as we try to find roots of a polynomial, which are those values of a polynomial that restrict the shape of the polynomial, eigenvectors are those vectors that try to prevent a linear transformation from happening in the vector space, and eigenvalues represent the magnitude of those eigenvectors. Now, since we have an intuitive understanding of the concept, we can look at the more mathematical elements and the calculation.
A vector is called an eigenvector of an operator K if the following relation is satisfied:
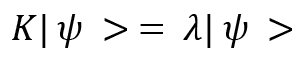
Here,  is the eigenvector and
is the eigenvector and  is the associated eigenvalue, which is also a complex number. If the eigenvectors of an operator represent the computational basis, then any state
is the associated eigenvalue, which is also a complex number. If the eigenvectors of an operator represent the computational basis, then any state  can be written as the linear combination of the eigenvectors associated with the operator K. This is true for diagonal matrices, where there are only diagonal entries and the rest of the elements are zero. The inverse of a diagonal matrix is as simple as just taking a reciprocal value of the diagonal elements. This makes a lot of practical applications simpler.
can be written as the linear combination of the eigenvectors associated with the operator K. This is true for diagonal matrices, where there are only diagonal entries and the rest of the elements are zero. The inverse of a diagonal matrix is as simple as just taking a reciprocal value of the diagonal elements. This makes a lot of practical applications simpler.
Now we will show the calculation process for eigenvalues and eigenvectors. Let's consider a 2x2 matrix; let's define a matrix A:
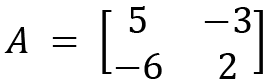
The characteristic equation for A that is used to calculate eigenvalues is given by the following:
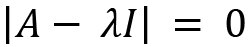
We apply the values of A and the identity matrix:
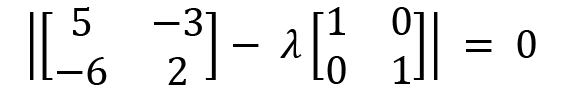
Simplifying further, we will get the following:
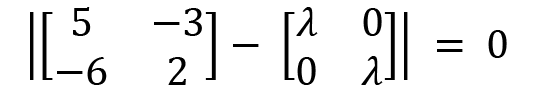
Now, subtracting  from A, we have the following:
from A, we have the following:
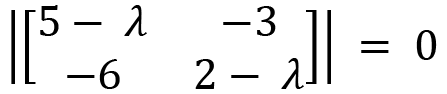
Now we will use the following relation to gain the characteristic equation of this matrix by calculating the determinant:
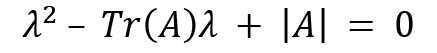
Here  and
and  , so we get the equation as follows:
, so we get the equation as follows:
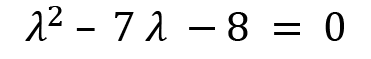
If we factorize the preceding characteristic equation, then we will get this:
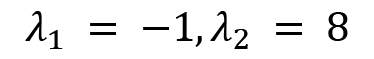
These are the eigenvalues of the operatorA.
Now we will move on to calculating the eigenvectors. Let  , and let's put this value into the following equation:
, and let's put this value into the following equation:
(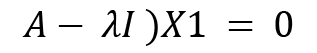
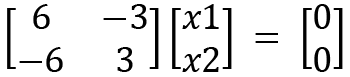
The equations can be formed as follows:
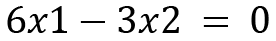
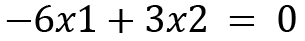
Since both the equations are the same, by simplifying and solving further, we will get the following:

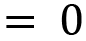
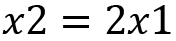
Now we can choose a value for  to have the eigenvectors. The simplest value is 1. Then, we will have the eigenvector
to have the eigenvectors. The simplest value is 1. Then, we will have the eigenvector  . In a very similar process,
. In a very similar process,  ; you can verify it yourself.
; you can verify it yourself.
Let's now consider solving an example for a 3x3 matrix also. We will define a matrix called A:
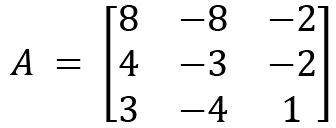
The characteristic equation for A that is used for calculating eigenvalues is as follows:
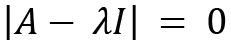
We then apply the values of A and the identity matrix:
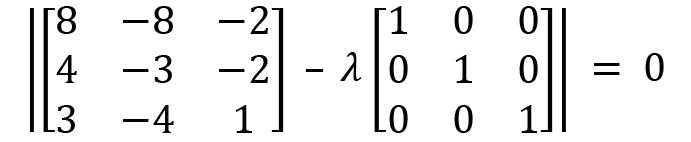
Simplifying a bit gives us the following:
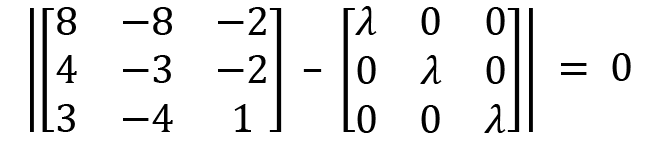
Subtracting  from A, we have this:
from A, we have this:
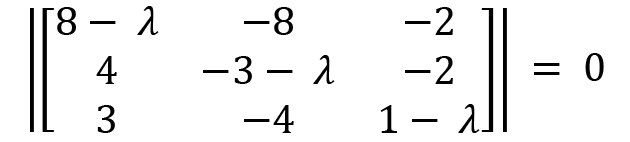
We will use a technique to simplify the calculations to calculate the determinant of this large matrix, which is as follows:
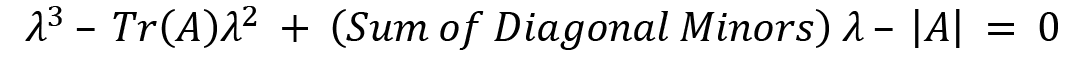
For calculating the minors, we just hide the rows and columns for the element for which we want to calculate the minor and then take the determinant of the remaining values.
Considering  , we hide the first row and the first column, and the remaining elements become the following:
, we hide the first row and the first column, and the remaining elements become the following:
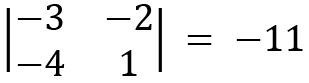
For  3, we hide the second row and the second column, and the remaining elements become this:
3, we hide the second row and the second column, and the remaining elements become this:
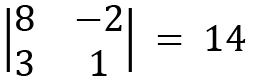
For  1, we get the following:
1, we get the following:
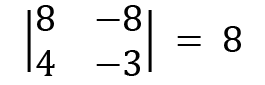
Therefore, the sum of the diagonal becomes  . The trace of
. The trace of  .
.
The final relation is this:
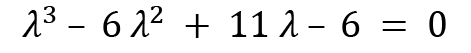
A calculator can be utilized to calculate the roots of this polynomial, and by doing so, you will get the roots of this cubic polynomial as follows:
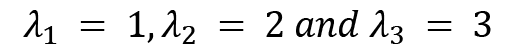
These are the eigenvalues of the operator A.
We will start by calculating the eigenvectors for A. We will start with  and put this value in the following equation:
and put this value in the following equation:
(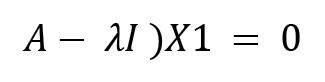
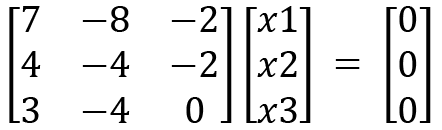
We will now utilize Cramer's rule to solve the preceding system of linear equations.
Consider any two rows or columns in the preceding matrix where adding or subtracting the values does not give 0 as an answer:
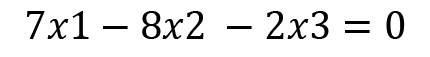
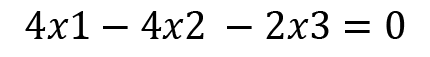
We can write  as the numerators and then write the determinants as the respective denominators, where the entries are coefficients from the other variables. This can be done as follows:
as the numerators and then write the determinants as the respective denominators, where the entries are coefficients from the other variables. This can be done as follows:
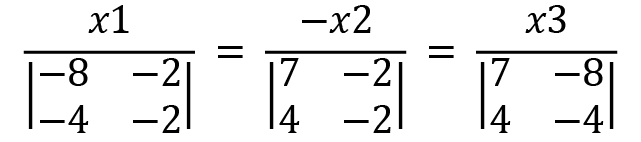
We observe that for  , we take the coefficients of
, we take the coefficients of  and
and  as the determinant entries by hiding the
as the determinant entries by hiding the  terms. A similar process is done for others as well.
terms. A similar process is done for others as well.
Solving the equation further, we will get the following result:
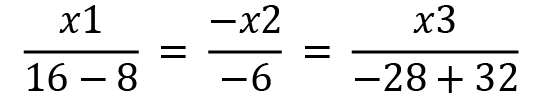
After solving a bit more, we have the following equation:
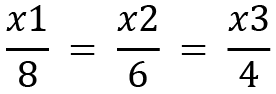
Therefore, the eigenvector  , which can be simplified further to be
, which can be simplified further to be  .
.
Similarly, for  .
.
We saw how to calculate the eigenvalues and eigenvectors of matrices/operators. Next, we are going to discuss an important concept known as tensor products.
Tensor products
In quantum computing, we often have to deal with two, three, or multi-qubit systems instead of only one qubit. A two-qubit system would be  , for example. Similarly, a three-qubit system would be
, for example. Similarly, a three-qubit system would be  . To deal with such composite systems, we use tensor products, which help us in performing various mathematical calculations on composite systems. The formal definition of a tensor product, as provided by An Introduction to Quantum Computing, is as follows:
. To deal with such composite systems, we use tensor products, which help us in performing various mathematical calculations on composite systems. The formal definition of a tensor product, as provided by An Introduction to Quantum Computing, is as follows:
The tensor product is a way of combining spaces, vectors or operators. An example is the union of two spaces H1 and H2 where each belongs to H, whose dimensions are n and m respectively. The tensor product of H1 H2 generates a new spacetime H of dimension nxm.
H2 generates a new spacetime H of dimension nxm.
You can find the referenced text in the Further reading section.
Let's now look at the calculation of tensor products for column vectors, which is the most common way of denoting a quantum state. Let's define two quantum states:
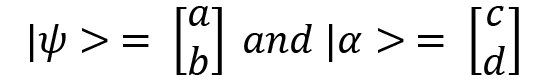
The tensor product of the two states is as follows:
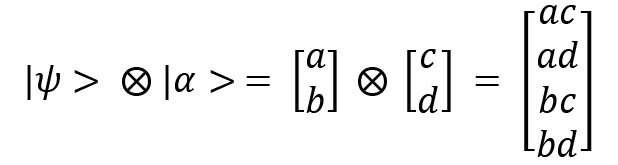
Using this, we can now describe the column vector representation of a two-qubit system. Suppose we consider  . This can be written like this:
. This can be written like this:
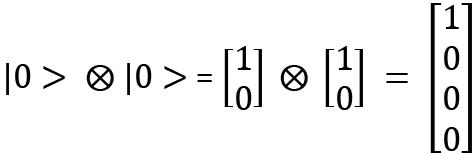
The tensor product has a distributive property, which is shown as follows:
 .
.
For example,  .
.
Proving all the properties of tensor products requires knowledge of abstract algebra and is out of the scope of this book. I highly recommend that you check out the books Finite-Dimensional Vector Space and Algebra by S. Lang (see the Further reading section) to gain a better understanding of the properties of tensor products.
The calculation of tensor products for two operators is given here. Let's define two 2x2 operators:
 and
and 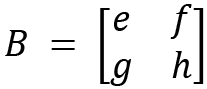
The tensor product of operators A and B is shown here:
Tensor products are very useful to verify the entanglement of quantum states. Entanglement is a useful property in quantum mechanics where two or more quantum systems can have some properties correlated with each other. As a consequence, knowing the properties of the first system can help to decipher the properties of the second system instantly.
With the conclusion of our discussion of tensor products, we also conclude our discussion of linear algebra. From the next section onward, we will discuss the visualization aspects of quantum computing, such as coordinate systems and complex numbers. We will also discuss probability theory in relation to quantum computing.
 United States
United States
 Great Britain
Great Britain
 India
India
 Germany
Germany
 France
France
 Canada
Canada
 Russia
Russia
 Spain
Spain
 Brazil
Brazil
 Australia
Australia
 Singapore
Singapore
 Canary Islands
Canary Islands
 Hungary
Hungary
 Ukraine
Ukraine
 Luxembourg
Luxembourg
 Estonia
Estonia
 Lithuania
Lithuania
 South Korea
South Korea
 Turkey
Turkey
 Switzerland
Switzerland
 Colombia
Colombia
 Taiwan
Taiwan
 Chile
Chile
 Norway
Norway
 Ecuador
Ecuador
 Indonesia
Indonesia
 New Zealand
New Zealand
 Cyprus
Cyprus
 Denmark
Denmark
 Finland
Finland
 Poland
Poland
 Malta
Malta
 Czechia
Czechia
 Austria
Austria
 Sweden
Sweden
 Italy
Italy
 Egypt
Egypt
 Belgium
Belgium
 Portugal
Portugal
 Slovenia
Slovenia
 Ireland
Ireland
 Romania
Romania
 Greece
Greece
 Argentina
Argentina
 Netherlands
Netherlands
 Bulgaria
Bulgaria
 Latvia
Latvia
 South Africa
South Africa
 Malaysia
Malaysia
 Japan
Japan
 Slovakia
Slovakia
 Philippines
Philippines
 Mexico
Mexico
 Thailand
Thailand
















