Chapter 1: Understanding the End-to-End Machine Learning Process
Welcome to the second edition of Mastering Azure Machine Learning. In this first chapter, we want to give you an understanding of what kinds of problems require the use of machine learning (ML), how the full ML process unfolds, and what knowledge is required to navigate this vast terrain. You can view it as an introduction to ML and an overview of the book itself, where for most topics we will provide you with a reference to upcoming chapters so that you can easily find your way around the book.
In the first section, we will ask ourselves what ML is, when we should use it, and where it comes from. In addition, we will reflect on how ML is just another form of programming.
In the second section, we will lay the mathematical groundwork you require to process data, and we will understand that the data you work with probably cannot be fully trusted. Further, we will look at different classes of ML algorithms, how they are defined, and how we can define the performance of a trained model.
Finally, in the third section, we will have a look at the end-to-end process of an ML project. We will understand where to get data from, how to preprocess data, how to choose a fitting model, and how to deploy this model into production environments. This will also get us into the topic of ML operations, known as MLOps.
In this chapter, we will cover the following topics:
- Grasping the idea behind ML
- Understanding the mathematical basis for statistical analysis and ML modeling
- Discovering the end-to-end ML process
Grasping the idea behind ML
The terms artificial intelligence (AI) and—partially—ML are omnipresent in today's world. However, a lot of what is found under the term AI is often nothing more than a containerized ML solution, and to make matters worse, ML is sometimes unnecessarily used to solve something extremely simple.
Therefore, in this first section, let's understand the class of problems ML tries to solve, in which scenarios to use ML, and when not to use it.
Problems and scenarios requiring ML
If you look for a definition of ML, you will often find a description such as this: It is the study of self-improving machine algorithms using data. ML is basically described as an algorithm we are trying to evolve, which in turn can be seen as one complex mathematical function.
Any computer process today follows the simple structure of the input-process-output (IPO) model. We define allowed inputs, we define a process working with those inputs, and we define an output through the type of results the process will show us. A simple example would be a word processing application, where every keystroke will result in a letter shown as the output on the screen. A completely different process might run in parallel to that one, having a time-based trigger to store the text file periodically to a hard disk.
All these processes or algorithms have one thing in common—they were manually written by someone using a high-level programming language. It is clear which actions need to be done when someone presses a letter in a word processing application. Therefore, we can easily build a process in which we implement which input values should create which output values.
Now, let's look at a more complex problem. Imagine we have a picture of a dog and want an application to just say: This is a dog. This sounds simple enough, as we know the input picture of a dog and the output value dog. Unfortunately, our brain (our own machine) is far superior to the machines we built, especially when it comes to pattern recognition. For a computer, a picture is just a square of  pixels, each containing three color channels defined by an 8-bit or 10-bit value. Therefore, an image is just a bunch of pixels made up of vectors for the computer, so in essence, a lot of numbers.
pixels, each containing three color channels defined by an 8-bit or 10-bit value. Therefore, an image is just a bunch of pixels made up of vectors for the computer, so in essence, a lot of numbers.
We could manually start writing an algorithm that maybe clusters groups of pixels, looks for edges and points of interest, and eventually, with a lot of effort, we might succeed in having an algorithm that finds dogs in pictures. That is when we get a picture of a cat.
It should be clear to you by now that we might run into a problem. Therefore, let's define one problem that ML solves, as follows:
Building the desired algorithm for a required solution programmatically is either extremely time-consuming, completely unfeasible, or impossible.
Taking this description, we can surely define good scenarios to use ML, be it finding objects in images and videos or understanding voices and extracting their intent from audio files. We will further understand what building ML solutions entails throughout this chapter (and the rest of the book, for that matter), but to make a simple statement, let's just acknowledge that building an ML model is also a time-consuming matter.
In that vein, it should be of utmost importance to avoid ML if we have the chance to do so. This might be an obvious statement, but as we (the authors) can attest, it is not for a lot of people. We have seen projects realized with ML where the output could be defined with a simple combination of if statements given some input vectors. In such scenarios, a solution could be obtained with a couple of hundred lines of code. Instead, months of training and testing an ML algorithm occurred, costing a lot of time and resources.
An example of this would be a company wanting to predict fraud (stolen money) committed by their own employees in a retail store. You might have heard that predicting fraud is a typical scenario for ML. Here, it was not necessary to use ML, as the company already knew the influencing factors (length of time the cashier was open, error codes on return receipts, and so on) and therefore wanted to be alerted when certain combinations of these factors occurred. As they knew the factors already, they could have just written the code and be done with it. But what does this scenario tell us about ML?
So far, we have looked at ML as a solution to solve a problem that, in essence, is too hard to code. Looking at the preceding scenario, you might understand another aspect or another class of problems that ML can solve. Therefore, let's add a second problem description, as follows:
Building the desired algorithm for a required solution is not feasible, as the influencing factors for the outcome of the desired outputs are only partially known or completely unknown.
Looking at this problem, you might now understand why ML relies so heavily on the field of statistics as, through the application of statistics, we can learn how data points influence one another, and therefore we might be able to solve such a problem. At the same time, we can build an algorithm that can find and predict the desired outcome.
In the previously mentioned scenario for detecting fraud, it might be prudent to still use ML, as it may be able to find a combination of influencing factors no one has thought about. But if this is not your set goal—as it was not in this case—you should not use ML for something that is easily written in code.
Now that we have discussed some of the problems solved by ML and have had a look at some scenarios for ML, let's have a look at how ML came to be.
The history of ML
To understand ML as a whole, we must first understand where it comes from. Therefore, let's delve into the history of ML. As with all events in history, different currents are happening simultaneously, adding pieces to the whole picture. We'll now look at a few important pillars that birthed the idea of ML as we know it today.
Learnings from neuroscience
A neuropsychologist named Donald O. Hebb published a book titled The Organization of Behavior in 1949. In this book, he described his theory of how neurons (neural cells) in our brain function, and how they contribute to what we understand as learning. This theory is known as Hebbian learning, and it makes the following proposition:
This basically describes that there is a process where one cell excites another repeatedly (the initiating cell) and maybe even the receiving cell is changed through a hidden process. This process is what we call learning.
To understand this a bit more visually, let's have a look at the biological structure of a neuron, as follows:
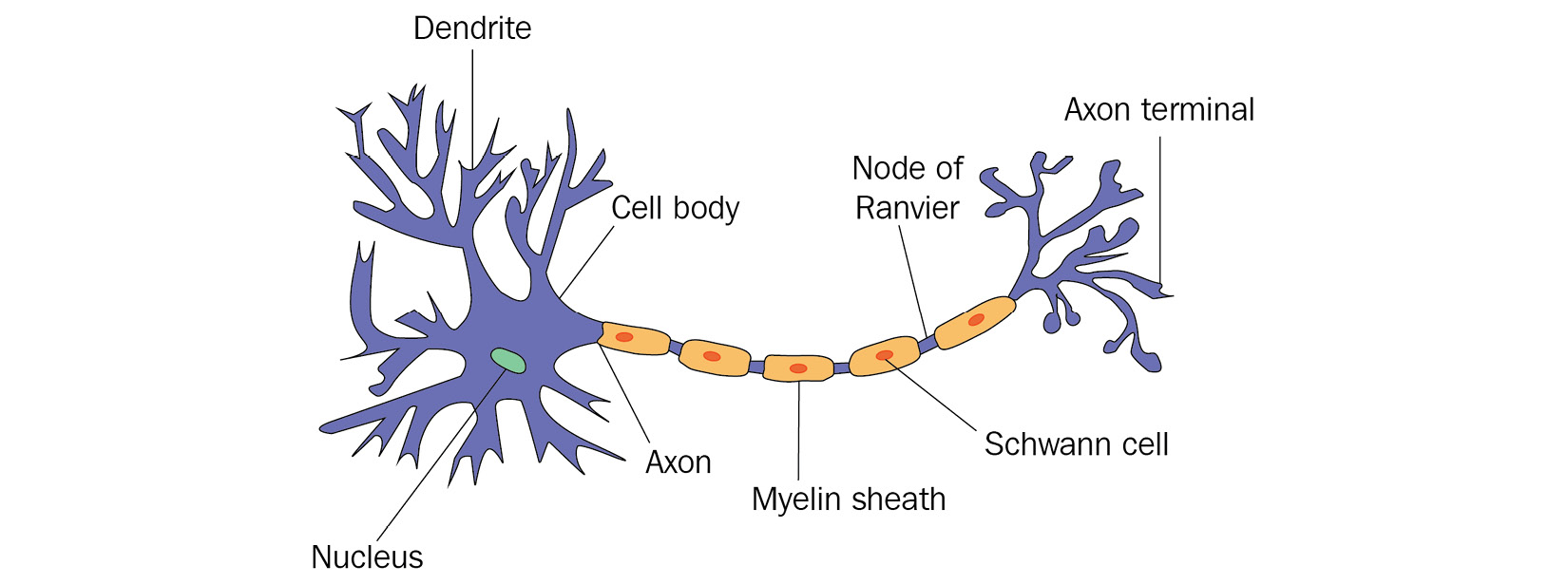
Figure 1.1 – Neuron in a biological neural network
What is visualized here? Firstly, on the left, we see the main body of the cell and its nucleus. The body receives input signals through dendrites that are connected to other neurons. In addition, there is a larger exit perturbing from the body called the axon, which connects the main body through a chain of Schwann cells to the so-called axon terminal, which in turn connects again to other neurons.
Looking at this structure with some creativity, it certainly resembles what a function or an algorithm might be. We have input signals coming from external neurons, we have some hidden process happening with these signals, and we have an output in the form of an axon terminal that connects the results to other neurons, and therefore other processes again.
It would take another decade again for someone to realize this connection.
Learnings from computer science
It is hard to talk about the history of ML in the context of computer science without mentioning one of the fathers of modern machines, Alan Turing. In a paper called Computing Machinery and Intelligence published in 1950, Turing defines a test called the Imitation Game (later called the Turing test) to evaluate whether a machine shows human behavior indistinguishable from a human. There are multiple iterations and variants of the test, but in essence, the idea is that a person would at no point in a conversation get the feeling they are not speaking with a human.
Certainly, this test is flawed, as there are ways to give relatively intelligent answers to questions while not being intelligent at all. If you want to learn more about this, have a look at ELIZA built by Joseph Weizenbaum, which passed the Turing test.
Nevertheless, this paper triggered one of the first discussions on what AI could be and what it means that a machine can learn.
Living in these exciting times, Arthur Samuel, a researcher working at International Business Machines Corporation (IBM) at that time, started developing a computer program that could make the right decisions in a game of checkers. In each move, he let the program evaluate a scoring function that tried to measure the chances of winning for each available move. Limited by the available resources at the time, it was not feasible to calculate all possible combinations of moves all the way to the end of the game.
This first step led to the definition of the so-called minimax algorithm and its accompanying search tree, which can commonly be used for any two-player adversarial game. Later, the alpha-beta pruning algorithm was added to automatically trim the tree from decisions that did not lead to better results than the ones already evaluated.
We are talking about Arthur Samuel, as it was he who coined the name machine learning, defining it as follows:
Combining these first ideas of building an evaluation function for training a machine and the research done by Donald O. Hebb in neuroscience, Frank Rosenblatt, a researcher at the Cornell Aeronautical Laboratory, invented a new linear classifier that he called a perceptron. Even though his progress in building this perceptron into hardware was relatively short-lived and would not live up to its potential, its original definition is nowadays the basis for every neuron in an artificial neural network (ANN).
Therefore, let's now dive deeper into understanding how ANNs work and what we can deduce about the inner workings of an ML algorithm from them.
Understanding the inner workings of ML through the example of ANNs
ANNs, as we know them today, are defined by the following two major components, one of which we learned about already:
- The neural network: The base structure of the system. A perceptron is basically an NN with only one neuron. By now, this structure comes in multiple facets, often involving hidden layers of hundreds of neurons, in the case of deep neural networks (DNNs).
- The backpropagation function: A rule for the system to learn and evolve. An idea thought of in the 1970s came into appreciation through a paper called Learning Representations by Back-Propagating Errors by D. Rumelhart, Geoffrey E. Hinton, Ronald J. Williams in 1986.
To understand these two components and how they work in tandem with each other, let's have a deeper look at both.
The neural network
First, let's understand how a single neuron operates, which is very close to the idea of a perceptron defined by Rosenblatt. The following diagram shows the inner workings of such an artificial neuron:

Figure 1.2 – Neuron in an ANN
We can clearly see the similarities to a real neuron. We get inputs from the connected neurons called  . Each of those inputs is weighted with a corresponding weight
. Each of those inputs is weighted with a corresponding weight 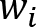 , and then, in the neuron itself, they are all summed up, including a bias
, and then, in the neuron itself, they are all summed up, including a bias  . This is often referred to as the net input function.
. This is often referred to as the net input function.
As the final operation, a so-called activation function 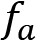 is applied to this net input that decides how the output signal of the neuron should look. This function must be continuous and differentiable and should typically create results in the range of [0:1] or [-1:1] to keep results scaled. In addition, this function could be linear or non-linear in nature, even though using a linear activation function has its downfalls, as described next:
is applied to this net input that decides how the output signal of the neuron should look. This function must be continuous and differentiable and should typically create results in the range of [0:1] or [-1:1] to keep results scaled. In addition, this function could be linear or non-linear in nature, even though using a linear activation function has its downfalls, as described next:
- You cannot learn a non-linear relationship presented in your data through a system of linear functions.
- A multilayered network made up of nodes with only linear activation functions can be broken down to just one layer of nodes with one linear activation function, making the network obsolete.
- You cannot use a linear activation function with backpropagation, as this requires calculating the derivative of this function, which we will discuss next.
Commonly used activation functions are sigmoid, hyperbolic tangent (tanh), rectified linear unit (ReLU), and softmax. Keeping this in mind, let's have a look at how we connect neurons together to achieve an ANN. A whole network is typically defined by three types of layers, as outlined here:
- Input layer: Consists of neurons accepting singular input signals (not a weighted sum) to the network. Their weights might be constant or randomized depending on the application.
- Hidden layer: Consists of the types of neurons we described before. They are defined by an activation function and given weights to the weighted sum of the input signals. In DNNs, these layers typically represent specific transformation steps.
- Output layer: Consists of neurons performing the final transformation of the data. They can behave like neurons in hidden layers, but they do not have to.
These together result in a typical ANN, as shown in the following diagram:

Figure 1.3 – ANN with one hidden layer
With this, we build a generic structure that can receive some input, realize some form of mathematical function through different layers of weights and activation functions, and in the end, hopefully show the correct output. This process of pushing information through the network from inputs to outputs is typically referred to as forward propagation. This, of course, only shows us what is happening with an input that passes through the network. The following question remains: How does it learn the desired function in the first place? The next section will answer this question.
The backpropagation function
The question that should have popped up in your mind by now is: How do we define the correct output? To have a way to change the behavior of the network, which mostly boils down to changing the values of the weights in the system, don't we need a way to quantize the error the system made?
Therefore, we need a function describing the error or loss, referred to as a loss function or error function. You might have even heard another name—a cost function. Let's define them next.
Loss Function versus Cost Function
A loss function (error function) computes the error for a single training example. A cost function, on the other hand, averages all loss function results for the entire training dataset.
This is the correct definition for those terms, but they are often used interchangeably. Just keep in mind that we are using some form of metric to measure the error we made or the distance we have from the correct results.
In classic backpropagation and other ML scenarios, the mean squared error (MSE) between the correct 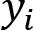 and the computed
and the computed  is used to define the error or loss of the operation. The obvious target is to now minimize this error. Therefore, the actual task to perform is to find the total minimum of this function in n-dimensional space.
is used to define the error or loss of the operation. The obvious target is to now minimize this error. Therefore, the actual task to perform is to find the total minimum of this function in n-dimensional space.
To do this, we use something that is often referred to as an optimizer, defined next.
Optimizer (Objective Function)
An optimizer is a function that implements a specific way to reach the objective of minimizing the cost function.
One such optimizer is an iterative process called gradient descent. Its idea is visualized in the following screenshot:

Figure 1.4 – Gradient descent with loss function influenced by only one input (left: finding global minimum, right: stuck in local minimum)
In gradient descent, we try to navigate an n-dimensional loss function by taking reasonably large enough steps, often defined by a learning rate, with the goal to find the global minimum, while avoiding getting stuck in a local minimum.
Keeping this in mind and without going into too much detail, let's finish this thought by going through the steps the backpropagation algorithm performs on the neural network. These are set out here:
- Pass a pair
 through the network (forward propagation).
through the network (forward propagation). - Compute the loss between the expected
 and the computed
and the computed  .
. - Compute all derivatives for all functions and weights throughout the layers using a mathematical chain rule.
- Update all weights beginning from the back of the network to the front, with slightly changed weights defined by the optimizer.
- Repeat until convergence is achieved (the weights are not receiving any meaningful updates anymore).
This is, in a nutshell, how an ANN learns. Be aware that it is vital to constantly change the pairs in Step 1, as otherwise, you might push the network too far into memorizing these couple of pairs you constantly showed it. We will discuss the phenomenon of overfitting and underfitting later in this chapter.
As a final step in this section, let's now bring together what we have learned so far about ML and what this means for building software solutions in the future.
ML and Software 2.0
What we learned so far is that ML seems to be defined by a base structure with various knobs and levers (settings and values) that can be changed. In the case of ANNs, that would be the structure of the network itself and the weights, bias, and activation function we can set in some regard.
Accompanying this base structure is some sort of rule or function as to how these knobs and levers should be transformed through a learning process. In the case of ANNs, this is defined through the backpropagation function, which combines a loss function with an optimizer and some math.
In 2017, Andrej Karpathy, the chief technical officer (CTO) of Tesla's AI division, proposed that the aforementioned idea could be just another way of programming, which he called Software 2.0 (https://karpathy.medium.com/software-2-0-a64152b37c35).
Up to this point, writing software was about explaining to the machine precisely what it must do and what outcome it must produce through defining specific commands it had to follow. In this classical software development paradigm, we define algorithms by their code and let data run through it, typically written in a reasonably readable language.
Instead of doing that, another idea could be to define a program we build by a base structure, a way to evolve this structure, and the type of data it must process. In this case, we get something very human-unfriendly to understand (an ANN with weights, for example), but it might be much better to understand for a machine.
So, we leave you at the end of this section with the thought that Andrej wanted to convey. Perhaps ML is just another form of programming machines.
Keeping all this in mind, let's now talk about math.
Understanding the mathematical basis for statistical analysis and ML modeling
Looking at what we have learned so far, it becomes abundantly clear that ML requires an ample understanding of mathematics. We already came across multiple mathematical functions we have to handle. Think about the activation function of neurons and the optimizer and loss functions for training. On top of that, we have not talked about the second aspect of our new programming paradigm—the data!
To choose the right ML algorithm and derive a good metric for a loss function, we have to take apart the data points we work with. In addition, we need to bring in the data points in relation to the domain we are working with. Therefore, when defining the role of a data scientist, you will often find a visual like this one:

Figure 1.5 – Requirements for data scientists
In this section, we will concentrate on what is referred to in Figure 1.5 as statistical research. We will understand why we need statistics and what base information we can derive from a given dataset, learn what bias is and ways to avoid that, mathematically classify possible ML algorithms, and finally, discuss how we choose useful metrics to define the performance of our trained models.
The case for statistics in ML
As we have seen, we require statistics to clean and analyze our given data. Therefore, let's start by asking: What do we understand from the term "statistics"?
A typical example of something such as this would be the prediction for the results of an election you see during the campaign or shortly after voting booths close. At those points in time, we do not know the precise result of the full population but we can acquire a sample, sometimes referred to as an observation. We get that by asking people for responses through a questionnaire. Then, based on this subset, we make a sound prediction for the full population by applying statistical methods.
We learned that in ML, we are trying to let the machine figure out a mathematical function that fits our problem, such as this:

Thinking back to our ANN, 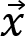 would be an input vector and
would be an input vector and  would be the resulting output vector. In ML jargon, they are known under a different name, as seen next.
would be the resulting output vector. In ML jargon, they are known under a different name, as seen next.
Features and Labels
One element of the input vector x is called a feature; the full output vector is called the label. Often, we only deal with a one-dimensional label.
Now, to bring this together, when training an ML model, we typically only have a sample of the given world, and as with any other time you are dealing with only a sample or subset of reality, you want to pick highly representative features and samples of the underlying population.
So, what does this mean? Let's think of an example. Imagine you want to train a small little robot car to be able to automatically drive through a tunnel. First, we need to think about what our features and labels in this scenario are. As features, we probably need something that measures the distance from the edges of the car to the tunnel in each direction, as we probably do not want to drive into the sides of the tunnel. Let's assume we have some infrared sensors attached to the front, the sides, and the back of the vehicle. Then, the output of our program would probably control the steering and the speed of the vehicle, which would be our labels.
Given that, as a next step, we should think of a whole bunch of scenarios in which the vehicle could find itself. This might be a simple scenario of the vehicle sitting straight-facing in the tunnel, or it could be a bad scenario where the vehicle is nearly stuck in a corner and the tunnel is going left or right from that point on. In all these cases, we read out the values of our infrared sensors and then do the more complicated tasks of making an educated guess as to how the steering has to be changed and how the motor has to operate. Eventually, we end up with a bunch of example situations and corresponding actions to take, which would be our training dataset. This can then be used to train an ANN so that the small car can learn how to follow a tunnel.
If you ever get the opportunity, try to perform this training. If you pick very good examples, you will understand the full power of ML, as you will most likely see something exciting, which I can attest to. In my setup, even though we never had a sample where we would instruct the vehicle to drive backward, the optimal function the machine trained had values where the vehicle learned to do exactly that.
In an example such as that, we would do everything from scratch and hopefully take representative samples by ourselves. In most cases you will encounter, the dataset already exists, and you need to figure out whether it is representative or whether we need to introduce additional data to achieve an optimal training result.
Therefore, let's have a look at some statistical properties you should familiarize yourself with.
Basics of statistics
We now understand that we need to be able to analyze the statistical properties of single features, derive their distribution, and analyze their relationship with other features and labels in the dataset.
Let's start with the properties of single features and their distribution. All the following operations require numerical data. This means that if you work with categorical data or something such as media files, you need to transform them into some form of numerical representation to get such results.
The following screenshot shows the main statistical properties you are after, their importance, and how you can calculate them:

Figure 1.6 – List of major statistical properties
From here onward, we can make the reasonable assumption that the underlying stochastic process follows a normal distribution. Be aware that this must not be the case, and therefore you should make yourself comfortable with other distributions (see https://www.itl.nist.gov/div898/handbook/eda/section3/eda36.htm).
The following screenshot shows a visual representation of a standard normal distribution:

Figure 1.7 – Standard normal distribution and its properties
Now, the strength of this normal distribution is that, based on the mean 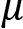 and standard deviation
and standard deviation  , we can make assumptions for the probabilities of samples to be in a certain range. As shown in Figure 1.7, there is a probability of around 68.27% for a value to have a distance from the mean of 1
, we can make assumptions for the probabilities of samples to be in a certain range. As shown in Figure 1.7, there is a probability of around 68.27% for a value to have a distance from the mean of 1 , 95.45% for a distance of
, 95.45% for a distance of 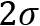 , and 99.73% for a distance of
, and 99.73% for a distance of  . Based on this, we can ask questions such as this:
. Based on this, we can ask questions such as this:
How probable is it to find a value with a distance of 5 from the mean?
from the mean?
Through questions such as this, we can start assessing whether what we see in our data is a statistical anomaly of the distribution, is a value that is simply false, or whether our suspected distribution is incorrect. This is done through a process called hypothesis testing, defined next.
Hypothesis Testing (Definition)
This is a method of testing if the so-called null hypothesis  is false, typically referring to the current suspected distribution. It means that the unlikely observation we encounter is pure chance. This hypothesis is rejected in favor of an alternative hypothesis
is false, typically referring to the current suspected distribution. It means that the unlikely observation we encounter is pure chance. This hypothesis is rejected in favor of an alternative hypothesis 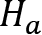 , if the probability falls below a predefined significance level (typically higher than
, if the probability falls below a predefined significance level (typically higher than  /lower than 5%). The alternative hypothesis thus presumes that the observation we have is due to a real effect that is not taken into account in the initial distribution.
/lower than 5%). The alternative hypothesis thus presumes that the observation we have is due to a real effect that is not taken into account in the initial distribution.
We will not go into further details on how to perform this test properly, but we urge you to familiarize yourself with this process thoroughly.
What we will talk about is the types of errors you can make in this process, as shown in the following screenshot:
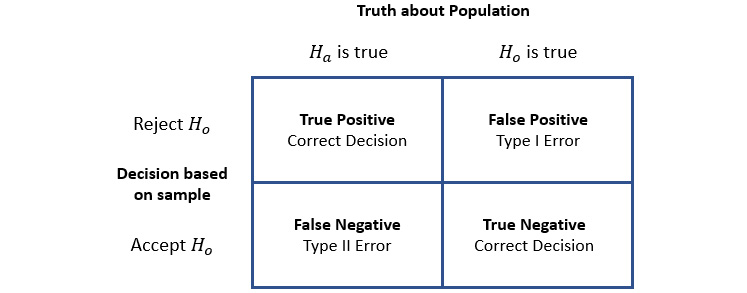
Figure 1.8 – Type I and Type II errors
We define the errors you see in Figure 1.8 as follows:
- Type I error: This denotes that we reject the hypothesis
 and the underlying distribution, even though it is correct. This is also referred to as a false-positive result or an alpha error.
and the underlying distribution, even though it is correct. This is also referred to as a false-positive result or an alpha error. - Type II error: This denotes that we do not reject the hypothesis
 and the underlying distribution, even though
and the underlying distribution, even though  is correct. This error is also referred to as a false-negative result or a beta error.
is correct. This error is also referred to as a false-negative result or a beta error.
You might have heard the term false positive before. Often, it comes up when you take a medical test. A false positive would denote that you have a positive result from a test, even though you do not have the disease you are testing for. As a medical test is also a stochastic process, as with nearly everything else in our world, the term is correctly used in this scenario.
At the end of this section, when we talk about errors and metrics in ML model training, we will come back to these definitions. As a final step, let's discuss relationships among features and between features and labels. Such a relationship is referred to as a correlation.
There are multiple ways to calculate a correlation between two vectors 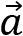 and
and  , but what they all have in common is that their results will fall in the range of [-1,1]. The result of this operation can be broadly defined by the following three categories:
, but what they all have in common is that their results will fall in the range of [-1,1]. The result of this operation can be broadly defined by the following three categories:
- Negatively correlated: The result leans toward -1. When the value of vector
 rises, the values of vector
rises, the values of vector  fall and vice versa.
fall and vice versa. - Uncorrelated: The result leans toward 0. There is no real interaction between vectors
 and
and  .
. - Positively correlated: The result leans toward 1. When the value of vector
 rises, the values of vector
rises, the values of vector  rise and vice versa.
rise and vice versa.
Through this, we can get an idea of relationships between data points, but please be aware of the differences between causation and correlation, as outlined next.
Causation versus Correlation
Even if two vectors are correlated with each other, it does not mean one of them is the cause of the other one—it simply means that one of them influences the other one. It is not causation as we probably don't see the full picture and every single influencing factor.
The mathematical theory we discussed so far should give you a good basis to build upon. In the next section, we will have a quick look at what kinds of errors we can make when taking samples, typically referred to as the bias in the data.
Understanding bias
At any stage of taking samples and when working with data, it is easily possible to introduce what is called bias. Typically, this influences the sampling quality and therefore has a big impact on any ML model we would like to fit to the data.
One example would be the causation versus correlation we just discussed. Seeing causation where none exists can have consequences in terms of the way you continue processing the data points. Other prominent biases that influence data are shown next:
- Selection bias: This bias happens when samples are taken that are not representative of the real-life distribution of data. This is the case when randomization is not properly done or when only a certain subgroup is selected for a study—for example, when a questionnaire about city planning is only given out to people in half of the neighborhoods of the city.
- Funding bias: This bias should be very well known and happens when a study or data project is funded by a sponsor and the results will therefore have a tendency toward the interests of the funding party.
- Reporting bias: This bias happens when only a selection of outcomes is represented in a dataset due to the fact that it is the tendency of people to underreport certain outcomes. Examples of this are given here: when you report bad weather events but not when there is sunshine; when you write negative reviews for a product but not positive reviews; when you only know about results written in your own language or from your own region but not from others.
- Observer bias/confirmation bias: This bias happens when someone favors results that confirm or support their own beliefs and values. Typically, this results in ignoring contrary information, not following the agreed guideline, or using ambiguous studies that support the existing preconceived opinion. The dangerous part here is that this can happen unconsciously.
- Exclusion bias: This bias happens when you remove data points during preprocessing that you consider irrelevant but are not. This includes removing null values, outliers, or other special data points. The removal might result in the loss of accuracy concerning the underlying real-life distribution.
- Automation bias: This bias happens when you favor results generated from automated systems over information taken from humans, even if they are correct.
- Overgeneralization bias: This bias happens when you project a property of your dataset toward the whole population. An example would be that you would assume that all cats have gray fur because in the large dataset you have, this is true.
- Group attribution bias: This bias happens when stereotypes are added as attributes to a whole group because of the actions of a few individuals within that group.
- Survivorship bias: This bias happens when you focus on successful examples while completely ignoring failures. An example would be that you study the competition of your company while ignoring all companies that failed, merged, or went bankrupt.
This list should give you a good understanding of problems that may arise when gathering and processing data. We can only urge you to read further into this topic while following these next guidelines.
Guidance for Handling Bias in Data
When using existing datasets, figure out the circumstances in which they were obtained to be able to judge their quality. When processing data either alone or in a team, define clear guidelines on how you define data and how you handle certain situations, and always reflect whether you are making assumptions based on your own predispositions.
To solidify your understanding that things are—most of the time—not as they seem, have a look at what is referred to as Simpson's paradox and the corresponding University of California (UC) Berkeley case (http://corysimon.github.io/articles/simpsons-paradox/).
Now that we have a good understanding of what to look out for when working with data, let's come back to the basics of ML.
Classifying ML algorithms
In the first section of this chapter, we got a glimpse into ANNs. These are special in the sense that they can be used in a so-called supervised or unsupervised training setup. To understand what is meant by this, let's define the current three major types of ML algorithms, as follows:
- Supervised learning: In supervised learning, models are trained with a so-called labeled dataset. That means besides knowing the input for the required algorithm, we also know the required output. This type of learning is split into two groups of problems—namely, classification problems and regression problems. Classification works with discrete results, where the output is a class or group, while regression works with continuous results, where the output would be a certain value. Examples of classification would be identifying fraud in money transactions or doing object detection in images. Examples of regression would be forecasting prices for houses or the stock market or predicting population growth. It is important to understand that this type of learning requires labels, which often results in the tedious task of labeling the whole dataset.
- Unsupervised learning: In unsupervised learning, models are trained on unlabeled data. This is basically self-organized learning to find patterns in data, referred to as clustering. Examples of this would be the filtering of spam emails in an inbox or the recommendation of movies or clothing a person might like to watch or purchase. Often, the learning algorithms are used in a real-time scenario where the data needs to be processed directly. The beauty of this type of learning is that we do not have to label the dataset.
- Reinforcement learning: In reinforcement learning, algorithms learn by reacting to a given environment on their own. The idea of this comes from how we as humans learn as we grow up. We did a certain action, and the outcome of that action was either good or bad or somewhere in between. We then either receive some sort of reward or we don't. Another similar example would be the way you would train a dog to behave. Technically, this is realized through a so-called agent that is guided by a policy map, deciding the probability to take actions when in a specific state. For the environment itself, we define a so-called state-value function that returns the value of being in a specific state. Good examples of this type of learning are training navigation control for a robot or an AI opponent for a game.
The following diagram provides an overview of the discussed ML types and the corresponding algorithms that are utilized in those areas:

Figure 1.9 – Types of ML algorithms
A detailed overview of many of the prominent ML algorithms can be found on the scikit-learn web page (https://scikit-learn.org/stable/), which is one of the major Python libraries for ML.
Now that we have an idea of the types of training we can perform, let's have a short look at what types of results we get from a training run and how to interpret them.
Analyzing errors and the quality of results of model training
As we discussed in the first section of this chapter, we require a loss function that we can minimize to optimize our training results. Typically, this is defined through what is referred to in mathematics as a metric. We need to differentiate at this point between metrics that are used to define a loss function and therefore used in an optimizer to train the model, and metrics that can be calculated to give additional hints toward the performance of the trained model. We will have a look at both kinds in this section.
As we have seen when looking at types of ML algorithms, we might work with an output represented by continuous data (regression), or we might work with an output represented by discrete data (classification).
The most prominent loss functions used in regression are MSE and root MSE (RMSE). Imagine you try to determine a fitted line for a bunch of samples in linear regression. The distance between the line and the sample point in two-dimensional (2D) space is your error. To calculate the RMSE for all data points, you would take the expected values 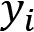 and the predicted values
and the predicted values  and calculate the following:
and calculate the following:

For classifications, this gets a little bit trickier. In most cases, the model can predict the correct class or cannot, making it a binary result. Further, we might have a binary classification problem (1 or 0—yes or no), or a multi-class problem (cat, dog, horse, and so on).
For both classification problems, there is a prominent loss function used called cross-entropy loss. To solve the problem of having a binary result, this loss function requires a model that outputs a probability 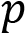 between 0 and 1 for a given data point
between 0 and 1 for a given data point 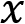 and a suggested prediction
and a suggested prediction  . For a binary classification model, it is calculated as follows:
. For a binary classification model, it is calculated as follows:
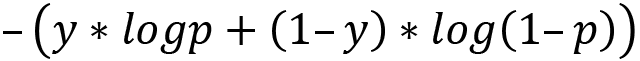
For multi-class classification, we sum up this error for all classes  , as follows:
, as follows:
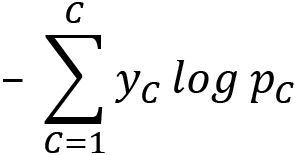
If you want to look further into this topic, consider other useful loss functions for regression, such as the absolute error loss and the Huber loss functions (used in support vector machines, or SVMs), useful loss functions for binary classification, such as the hinge loss function, and useful loss functions for multi-class classification, such as the Kullback-Leibler divergence (KL-divergence) function. The last one can also be used in RL as a metric to monitor the policy function during training.
Everything we have discussed so far requires something we can put into a mathematical formula. Imagine working with text files to build a model for natural language processing (NLP). In such a case, we do not have a useful mathematical representation for text besides something such as Unicode. We will learn in Chapter 7, Advanced Feature Extraction with NLP, how to represent it in a useful, vectorized manner. Having vectors, we can use a different kind of metric to calculate how similar vectors are, called the cosine similarity metric, which we will discuss in Chapter 6, Feature Engineering and Labeling.
So far, we have discussed how to calculate loss functions for a couple of scenarios, but how can we define the performance of our model overall?
For regression models, our loss function was defined over the whole corpus of our training set. The error of a single observation or prediction would be  . Therefore, RMSE is already a cost function and can be used by an optimizer to improve the model performance, so we can use it to judge the performance of the model.
. Therefore, RMSE is already a cost function and can be used by an optimizer to improve the model performance, so we can use it to judge the performance of the model.
For classification models, this gets a little bit more interesting. Cross-entropy can be used with an optimizer to train the model and can be used to judge the model, but besides that, we can define an additional metric to look out for.
Something obvious would be what is referred to as the accuracy of a model, calculated as follows:

Now, this looks about right. We just say that the quality of our model is the percentage of how often we guessed correctly, and the reality is that a lot of people agree with this statement. Remember when we defined false positives and false negatives? These now come into play. Let's look at an example.
Imagine a test that checks for a contagious virus. Figure 1.10 shows the results for 100 people being tested for this virus, including the correctness of the results:

Figure 1.10 – Test results for a group of 100 people
Now, what would be the accuracy of this test given these results? Let's define it again using the values for true positive (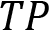 ), false positive (
), false positive ( ), false negative (
), false negative ( ), and true negative (
), and true negative (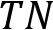 ) and calculate the results for our example, as follows:
) and calculate the results for our example, as follows:
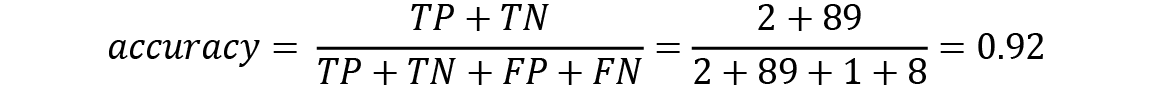
This sounds like a good test. It gives accurate results in 92% of cases, but perhaps you see the problem here. Accuracy sees everything equally. Our test misclassifies someone having the virus eight times as someone being virus-free, which might have dire ramifications. That means it might be useful having performance metrics that put more emphasis on false-positive or false-negative outcomes. Therefore, let's define two additional metrics to calculate.
The first one we call precision, a value that defines how many positive identifications were correct. The formula is shown here:
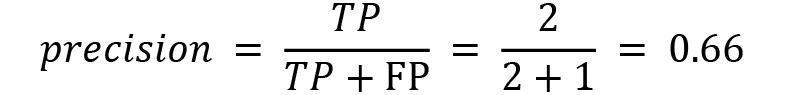
In our example, only in two out of three cases are we correct when we declare someone to be infected. A model with a precision value of 1 would have no false-positive results.
The second one we call recall, a value that defines how many positive results we identify correctly. The formula is shown here:

This means in our example, we correctly identify 20% of all infected patients, which is a bad result. A model with a recall value of 1 would have no false-negative results.
To evaluate our test or classification correctly, we need to evaluate accuracy, precision, and recall. Be aware that, as mentioned when we talked about hypothesis testing, precision and recall can work against each other. Therefore, you often have to decide whether you prefer to be precise when saying "You have the virus" or whether you prefer to find everyone who has the virus. You might now understand why such tests are often designed toward recall.
With this, we conclude the section on the mathematical basis required to get better at building ML models and working with data. Based on what we have learned so far, you should take the next point with you.
Important Note
Never just use methods from ML libraries for data analysis and modeling; understand them mathematically.
In the next section, we will guide you through the structure of the end-to-end ML process and the structure of this book.
Discovering the end-to-end ML process
We have finally arrived at the main topic of this chapter. After reviewing the past and understanding the purpose of ML and how it takes its roots in mathematical data analysis, let's now get a clear picture of which steps need to be taken to create a high-quality ML model.
The following diagram shows an overview of the (sometimes recursive) steps from data to model to deployed model:

Figure 1.11 – End-to-end ML process
Looking at this flow, we can define the following distinct steps to take:
- Excavating data and sources
- Preparing and cleaning data
- Defining labels and engineering features
- Training models
- Deploying models
These show the steps for running one single ML project. When you deal with a lot of projects and data, it becomes increasingly important to adopt some form of automation and operationalization, which is typically referred to as MLOps.
In this section, we will give an overview of each of these steps, including MLOps and its importance, and explain in which chapters we will delve deeper into the corresponding topic. Before we start going through those steps, reflect on the following question:
As a percentage, how much time would you put aside for each of those steps?
After you are done, have a look at the following screenshot, which shows you the typical time investment required for those tasks:

Figure 1.12 – ML time invested
Was your guess reasonably close to this? You might be surprised that only 20% of the time, you will work on something that has to do with the actual training and deployment of ML models. Therefore, you should take the next point to heart.
Important Note
In an ML project, you should spend most of your time taking apart your datasets and finding other useful data sources.
Failure to do so will have ramifications on the quality of your model and its performance. Now, having said that, let's go through the steps one by one, starting with where to source your data from.
Excavating data and sources
When you start an ML project, you probably have some outcome in mind, and often, you have some form of existing dataset you or your company wants to start with. This is where you start familiarizing yourself with the given data, understanding what you have and what is missing by doing analysis, which we will come back to in the following steps.
At some point, you might realize that you are missing additional—but crucial—data points to increase the quality of your results. This highly depends on what you are missing—whether it is something you or your company can obtain or whether you need to find it somewhere else. To give you some ideas, let's have a look at the following options to acquire additional data and what you should be aware of:
- In-house data sources: If you are running this project in or with a company, the first point to look is internally. Advantages of this are that it is free of charge, it is often standardized, and you should be able to find a person that knows this data and how it was obtained. Depending on the project, it might also be the only place you can acquire the required data. Disadvantages of this option are that you might not find what you are looking for, that the data is poorly documented, and that the quality might be in question due to bias in the data.
- Open data sources: Another option is to use freely available datasets. Advantages of those are that they are typically gigantic in size (terabytes (TB) of data), they cover different time periods, and they are typically well structured and documented. Disadvantages are that some data fields might be hard to understand (and the creator is not available), the quality might also vary due to bias in the data, and often when used, they require you to publish your results. Examples of this would be the National Oceanic and Atmospheric Administration (NOAA) (https://www.ncei.noaa.gov/weather-climate-links) and the European Union (EU) Open Data Portal (https://data.europa.eu/en), among many others.
- Data seller (data as a service, or DaaS): A final option would be to buy data from a data seller, either by purchasing an existing dataset or by requesting the creation of one. Advantages of this option are that it saves you time, it can give you access to an individualized dataset, and you might even get access to preprocessed data. Disadvantages are that this is expensive, you still need to do all the other following steps to make this data useful, and there might be questions concerning privacy and ethics.
Now that we have a good idea of where to get data initially or additionally, let's look at the next step: preparing and cleaning the data.
Preparing and cleaning data
As alluded to before, descriptive data exploration is without a doubt one of the most important steps in an ML project. If you want to clean data and build derived features or select an ML algorithm to predict a target variable in your dataset, then you need to understand your data first. Your data will define many of the necessary cleaning and preprocessing steps. It will define which algorithms you can choose, and it will ultimately define the performance of your predictive model.
The exploration should be done as a structured analytical process rather than a set of experimental tasks. Therefore, we will go through a checklist of data exploration tasks that you can perform as an initial step in every ML project, before starting any data cleaning, preprocessing, feature engineering, or model selection. By applying these steps, you will be able to understand the data and gain knowledge about the required preprocessing tasks.
Along with that, it will give you a good estimate of what kinds of difficulties you can expect in your prediction task, which is essential for judging the required algorithms and validation strategies. You will also gain an insight into which possible feature engineering methods could apply to your dataset and have a better understanding of how to select a good loss function.
Let's have a look at the required steps.
Storing and preparing data
Your data might come in a variety of different formats. You might work with tabular data stored in a comma-separated values (CSV) file; you might have images stored as Joint Photographic Experts Group (JPEG) or Portable Network Graphics (PNG) files, text stored in a JavaScript Object Notation (JSON) file, or audio files in MP3 or M4V format. CSV can be a good format as it is human-readable and can be parsed efficiently. You can open and browse it using any text editor.
If you work on your own, you might just store this raw data in a folder on your system, but when you are working with a cloud infrastructure or even just a company infrastructure in general, you might need some form of cloud storage. Certainly, you can just upload your raw data by hand to such storage, but often, the data you work with is coming from a live system and needs to be extracted from there. This means it might be worthwhile having a look at so-called extract-transform-load (ETL) tools that can automate this process and bring the required raw data into cloud storage.
After all of the preprocessing steps are done, you will have some form of layered data in your storage, from raw to cleaned to labeled to processed datasets.
We will dive deeper into this topic in Chapter 4, Ingesting Data and Managing Datasets. For now, just understand that we will automate this process of making data available for processing.
Cleaning data
In this step, we have a look at inconsistency and structural errors in the data itself. This step is often required for tabular data and sometimes text files, but not so much for image or audio files. For the latter, we might be able to crop images and change their brightness or contrast, but it might be required to go back to the source to create better-quality samples. The same goes for audio files.
For tabular datasets, we have much more options for processing. Let's go through what to look out for, as follows:
- Duplicates: Through mistakes in copying data or due to a combination of different data sources, you might find duplicate samples. Typically, copies can be deleted. Just make sure that these are not two different samples that look the same.
- Irrelevant information: In most cases, you will have datasets with a lot of different features, some of which will be completely unnecessary for your project. The obvious ones you should just remove in the beginning; others you will be able to remove later after analyzing the data further.
- Structural errors: This refers to the values you can see in the samples. You might run into different entries with the same meaning (such as
USandUnited States) or simply typos. These should be standardized or cleaned up. A good way to do this is by visualizing all available values of a feature. - Anomalies (outliers): This refers to very unlikely values for which you need to decide whether they are errors or actually true. This is typically done after analyzing the data when you know the distribution of a feature.
- Missing values: This refers to cells in your data that are either blank or have some generic value in them, such as
NAorNaN. There are different ways to rectify this besides deleting entire samples. It is also prudent to wait until you have more insight from analyzing the data, as you might see better ways to replace them.
After this step, we can start analyzing the cleaned version of our dataset further.
Analyzing data
In this step, we apply our understanding of statistics to get some insights into our features and labels. This includes calculating statistical properties for each feature, visualizing them, finding correlated features, and measuring something that is called feature importance, which calculates the impact of a feature on the label, also referred to as the target variable.
Through these methods, we get ideas about relationships among features and between features and targets, which can help us to make a decision. In this decision-making process, we also start adding something vitally important—our domain knowledge. If you do not know what the data represents, you will have a hard time pruning it and choosing optimal features and samples for training.
There are a lot more techniques that can be applied in this step, including something called dimensional reduction. If you have thousands of features (a numerical representation of an image, for example), it gets very complicated for humans and even for ML processes to understand relationships. In such cases, it might be useful to map this high-dimensional sample to a two-dimensional or three-dimensional representation in the form of a vector. Through this, we can easily find similarities in different samples.
We will dive deeper into the topics of cleaning and analyzing data in Chapter 5, Performing Data Analysis and Visualization.
Having done all these steps, we will have a good understanding of the data we have at hand, and we might already know what we are missing. As the final step in preprocessing our data, we will have a look at creating and transforming features, typically referred to as feature engineering, and creating labels when missing.
Defining labels and engineering features
In the second part of the preprocessing of data, we will discuss the labeling of data and the actions we can perform on features. To perform these steps, we need the knowledge obtained through the exploratory steps we've discussed so far. Let's start by looking at labeling data.
Labeling
Let's start with a bummer: this process is very tedious. Labeling, also called annotation, is the least exciting part of an ML project yet one of the most important tasks in the whole process. The goal is to feed high-quality training data into the ML algorithms.
While proper labels greatly help to improve prediction performance, the labeling process will also help you to study the dataset in greater detail. Let me clarify that labeling data requires deep insight and understanding of the context of the dataset and the prediction process, which you should have acquired at this point. If we were, for example, aiming to predict breast cancer using computerized tomography (CT) scans, we would also need to understand how breast cancer can be detected in CT images to label the data.
Mislabeling the training data has a couple of consequences, such as label noise, which you want to avoid as it will affect the performance of every downstream process in the ML pipeline. In some cases, your labeling methodology is dependent on the chosen ML approach for a prediction problem. A good example is the difference between object detection and segmentation, both of which require completely differently labeled data.
There are some techniques and tooling available to speed up the labeling process that make use of the fact that we can use ML algorithms not only for the desired project but also to learn how to label our data. Such models start proposing labels during your manual annotation of the dataset.
Feature engineering
In a nutshell, in this step, we will start transforming the features or adding new features. Obviously, we are not doing such actions on a whim, but rather due to the knowledge we gathered in the previous steps. We might have understood, for example, that the full date and time are far too precise, and we need just the day of the week or the month. Whatever it might be, we will try to shape and extract what we need.
Typically, we will perform one of the following actions:
- Feature creation: Create new features from a given set of features or from additional information sources.
- Feature transformation: Transform single features to make them useful and stable for the utilized ML algorithm.
- Feature extraction: Create derived features from the original data.
- Feature selection: Choose the most prominent and predictive features.
We will dive deeper into labeling and the multitude of methods to apply to our features in Chapter 6, Feature Engineering and Labeling. In addition, we will have a detailed look at a more complex example of feature engineering when working with text data in an NLP project. You will find this in Chapter 7, Advanced Feature Extraction with NLP.
We conclude this step by reiterating how important the whole preprocessing data steps are and how much influence they have on the next step, where we will discuss model training. Further, we remember that we might need to come back to this after model training in case of lackluster performance of our model.
Training models
We finally reached the point where we can bring ML algorithms into play. As with data experimentation and preprocessing, training an ML model is an analytical, step-by-step process. Each step involves a thought process that evaluates the pros and cons of each algorithm according to the results of the experimentation phase. As in every other scientific process, it is recommended that you come up with a hypothesis first and verify whether this hypothesis is true afterward.
Let's look at the steps that define the process of training an ML model, as follows:
- Define your ML task: First, we need to define the ML task we are facing, which most of the time is defined by the business decision behind your use case. Depending on the amount of labeled data, you can choose between unsupervised and supervised learning methods, as well as many other subcategories.
- Pick a suitable model: Pick a suitable model for the chosen ML task. This might be a logistical regression, a gradient-boosted ensemble tree, or a DNN, just to name a few popular ML model choices. The choice is mainly dependent on the training (or production) infrastructure (such as Python, R, Julia, C, and so on) and the shape and type of the data.
- Pick or implement a loss function and an optimizer: During the data experimentation phase, you should have already come up with a strategy on how to test your model performance. Hence, you should have picked a data split, loss function, and optimizer already. If you have not done so, you should at this point evaluate what you want to measure and optimize.
- Pick a dataset split: Splitting your data into different sets—namely, training, validation, and test sets—gives you additional insights into the performance of your training and optimization process and helps you to avoid overfitting your model to your training data.
- Train a simple model using cross-validation: When all the preceding choices are made, you can go ahead and train your ML model. Optimally, this is done as cross-validation on a training and validation set, without leaking training data into validation. After training a baseline model, it's time to interpret the error metric of the validation runs. Does it make sense? Is it as high or low as expected? Is it (hopefully) better than random and better than always predicting the most popular target?
- Tune the model: Finally, you can either tune the outcome of the model by working with the so-called hyperparameters of a model, do model stacking or other advanced methods, or you might have to go back to the initial data and work on that before training the model again.
These are the base steps we perform when training our model. In the following section, we will give some more insights into the aforementioned steps, starting with how to choose a model.
Choosing a model
When it comes to choosing a good model for your data, it is recommended that you favor simple traditional models before going toward the more complex options. An example would be ensemble models, such as gradient-boosted tree ensembles, when training data is limited. These models perform well on a broad set of input values (ordinal, nominal, and numeric) as well as training efficiently, and they are understandable.
Tree-based ensemble models combine many weak learners into a single predictor based on decision trees. This greatly reduces the problem of the overfitting and instability aspects of a single decision tree. The output, after a few iterations using the default parameter, usually delivers great baseline results for many different applications.
In Chapter 9, Building ML Models Using Azure Machine Learning, we dedicate a complete section to training a gradient-boosted tree ensemble classifier using LightGBM, a popular tree ensemble library from Microsoft.
To capture the meaning of large amounts of complex training data, we need large parametric models. However, training parametric models with many hundreds of millions of parameters is no easy task, due to exploding and vanishing gradients, loss propagation through such a complex model, numerical instability, and normalization. In recent years, a branch of such high-parametric models achieved extremely good results through many complex tasks—namely, deep learning (DL).
DL basically spans up a multilayer ANN, where each layer is seen as a certain step in the data processing pipeline of the model.
In Chapter 10, Training Deep Neural Networks on Azure, and Chapter 12, Distributed Machine Learning on Azure, we will delve deeper into how to train large and complex DL models on single machines and on a distributed GPU cluster.
Finally, you might work with a completely different form of data, such as audio or text data. In such cases, there are specialized ways to preprocess and score this data. One of these fields would be recommendation engines, which we will discuss thoroughly in Chapter 13, Building a Recommendation Engine in Azure.
Choosing a loss function and an optimizer
As we discussed in the previous section, there are many metrics to choose from, depending on the type of training and model you want to use. After looking at the relationship between the feature and target dimensions, as well as the separability of the data, you should continue to evaluate which loss function and optimizer you will use to train your model.
Many ML practitioners don't value the importance of a proper error metric highly enough and just use what is easy, such as accuracy and RMSE. This choice is critical. Furthermore, it is useful to understand the baseline performance and the model's robustness to noise. The first can be achieved by computing the error metric using only the target variable with the highest occurrence as a prediction. This will be your baseline performance. The second can be done by modifying the random seed of your ML model and observing the changes to the error metric. This will show you which decimal place you can trust the error metric to.
Keep in mind that it is prudent to evaluate the chosen error metric and any additional metric you desire after training runs, and experiment whether others might be more beneficial.
As for the optimizer, it highly depends on the model you chose as to which options you have in this regard. Just remember the optimizer is how we get to the target, and the target is defined by the loss function.
Splitting the dataset
Once you have selected an ML model, a loss function, and an optimizer, you need to think about splitting your dataset for training. Optimally, the data should be split into three disjointed sets: a training, a validation, and a test dataset. We use multiple sets to ensure that the model generalizes well on unseen data and that the reported error metric can be trusted. Hence, you can see that dividing the data into representative sets is a task that should be performed as an analytical process. These sets are defined as follows:
- Training dataset: The subset of data used to fit/train the model.
- Validation dataset: The subset of data used to provide an evaluation during training to tune hyperparameters. The algorithm sees this data during training, but never learns from it. Therefore, it has an indirect influence on the model.
- Test dataset: The subset of data used to run an unbiased evaluation of the trained model after training.
If training data leaks into the validation or testing set, you risk overfitting the model and skewing the validation and testing results. Overfitting is a problem that you must handle besides underfitting the model. Both are defined as follows:
Underfitting versus Overfitting
An underfitted model performs purely on the data. The reasons for that are often that the model is too simplistic to understand the relationship between the features and the target variables, or that your initial data is lacking useful features. An overfitted model performs perfectly on the training dataset and purely on any other data. The reason for that is that it basically memorized the training data and is unable to generalize.
There are different discussions on what the size of these splits should be and many different further techniques to choose samples for each category, such as stratified splitting (sampling based on class distributions), temporal splitting, and group-based splitting. We will take a deeper look at these in Chapter 9, Building ML Models Using Azure Machine Learning.
Running the model training
In most cases, you will not build an ANN structure and an optimizer from scratch. You will use ready-made ML libraries, such as scikit-learn, TensorFlow, or PyTorch. Most of these frameworks and libraries are written in Python, which should therefore be the language of choice for your ML projects.
When writing your code for model training, it is a good idea to logically divide the required code into two files, as follows:
- Authoring script (authoring environment): The script that defines the environment (libraries, training location, and so on) in which the ML training will take place and the one triggering the execution script
- Execution script (execution environment): The script that only contains the actual ML training
By splitting your code in this way, you avoid updating the actual training script when your target environment changes. This will make code versioning and MLOps much cleaner.
To understand what types of class methods we might encounter in an ML library, let's have a look at a short code snippet from TensorFlow here:
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),…])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=5)
model.evaluate(x_test, y_test)
Looking at this code, we see that we are using a model called Sequential that is a basic ANN defined by a sequential set of layers with one input and one output. We see in the model creation step that there are layers defined and some omitted other settings. In addition, in the compile() method, we define an optimizer, a loss function, and some additional metrics we are interested in. Finally, we see a method called fit() running on the training dataset and a method called evaluate() running on the test dataset. Now, what do these methods do exactly? Before we get to that, let's first define something.
Hyperparameters versus Parameters of a Model
There are two kinds of settings that are adjusted during model training. Settings such as the weights and the bias in an ANN are referred to as the parameters. They are changed during the training phase. Other settings—such as the activation functions and the number of layers in an ANN, the data split, the learning rate, or the chosen optimizer—are referred to as hyperparameters. Those are the meta settings we adjust before a training run.
Having this out of the way, let's define the typical methods you will encounter, as follows:
- Hyperparameter methods: These are methods used to define the characteristics of the model. They are often found in the constructor (as for the
Sequentialclass), in a special function such ascompile(), or they are part of the training method we discuss next. - Training method: Often named
fit()ortrain(), this is the main method that trains the parameter of the model based on the training dataset, the loss function, and the optimizer. These methods do not return any type of value—they just update the model object and its parameters. - Test method: Often named
evaluate(),transform(),score(), orpredict(). In most cases, these return some form of result, as they are typically running the test dataset against the trained model.
This is the typical structure of methods you will encounter for a model in an ML library. Now that we have a good idea of how to set up our coding environment and use available ML libraries, let's look at how to tune the model after our initial training.
Tuning the model
After we have trained a simple ensemble model that performs reasonably better than the baseline model and achieves acceptable performance according to the expected performance estimated during data preparation, we can progress with optimization. This is a point we really want to emphasize. It's strongly discouraged to begin model optimization and stacking when a simple ensemble technique fails to deliver useful results. If this is the case, it would be much better to take a step back and dive deeper into data analysis and feature engineering.
Common ML optimization techniques—such as hyperparameter optimization, model stacking, and even automated machine learning (AutoML)—help you get the last 10% of performance boost out of your model.
Hyperparameter optimization concentrates on changing the initial settings of the model training to improve its final performance. Similarly, model stacking is a very common technique used to improve prediction performance by putting a combination of multiple different model types into a single stacked model. Hence, the output of each model is fed into a meta-model, which itself is trained through cross-validation and hyperparameter tuning. By combining significantly different models into a single stacked model, you can always outperform a single model.
If you decide to use any of those optimization techniques, it is advised to perform them in parallel and fully automated on a distributed cluster. After seeing too many ML practitioners manually parametrizing, tuning, and stacking models together, we want to raise this important message: optimizing ML models is boring.
It should rarely be done manually as it is much faster to perform it automatically as an end-to-end optimization process. Most of your time and effort should go into experimentation, data preparation, and feature engineering—that is, everything that cannot be easily automated and optimized using raw compute power. We will delve deeper into the topic of model tuning in Chapter 11, Hyperparameter Tuning and Automated Machine Learning.
This concludes all important topics to know about model training. Next, we will have a look at options for the deployment of ML models.
Deploying models
Once you have trained and optimized an ML model, it is ready for deployment. This step is typically referred to as inferencing or scoring a model. Many data science teams, in practice, stop here and move the model to production as a Docker image, often embedded in a REpresentational State Transfer (REST) API using Flask or similar frameworks. However, as you can imagine, this is not always the best solution, depending on your requirements. An ML or data engineer's responsibility doesn't stop here.
The deployment and operation of an ML pipeline can be best seen when testing the model on live data in production. A test is done to collect insights and data to continuously improve the model. Hence, collecting model performance over time is an essential step to guaranteeing and improving the performance of the model.
In general, we differentiate two main architectures for ML-scoring pipelines, as follows:
- Batch scoring using pipelines: An offline process where you evaluate an ML model against a batch of data. The result of this scoring technique is usually not time-critical, and the data to be scored is usually larger than the model.
- Real-time scoring using a container-based web service endpoint: This refers to a technique where we score single data inputs. This is very common in stream processing, where single events are scored in real time. It's obvious that this task is highly time-critical, and the execution is blocked until the resulting score is computed.
We will discuss these two architectures in more detail in Chapter 14, Model Deployments, Endpoints, and Operations. There, we will also investigate an efficient way of collecting runtimes, latency, and other operational metrics, as well as model performance.
The model files we create, and the previously mentioned options, are typically defined by a standard hardware architecture. As mentioned, we probably create a Docker image that is deployed to a virtual machine (VM) or a web service. What if we want to deploy our model to a highly specialized hardware environment, such as a GPU or a field-programmable gate array (FPGA)?
To explore this further, we will dive deeper into alternative deployment targets and methods in Chapter 15, Model Interoperability, Hardware Optimization, and Integrations. There, we will have a look at a framework called Open Neural Network eXchange (ONNX) that allows us to convert our model into a standardized model format to be deployed to virtually any environment. Additionally, we have a look at FPGAs and why they might be a good deployment target for ML, and finally, we will explore other Azure services such as Azure IoT Edge and Power BI for integration.
This step wraps up the end-to-end process for a single ML model. Next, we will see a short overview of how to make such ML projects operational in an enterprise-grade environment using MLOps.
Developing and operating enterprise-grade ML solutions
To operationalize ML projects requires the use of automated pipelines and development-operations (DevOps) methodologies such as continuous integration (CI) and continuous delivery/continuous deployment (CD). These combined are typically referred to as MLOps.
When looking at the steps we performed in an ML project, we can see that there are typically two major operations happening—the training of a model and the deployment of a model. As these can happen independently of one another, it is worthwhile defining two different automated pipelines, as follows:
- Training pipeline: This includes loading datasets (possibly even including an ETL pipeline), transformation, model training, and registering final models. This pipeline could be triggered by changes in the dataset or possible detected data drift in a deployed model.
- Deployment pipeline: This includes loading of models from the registry, creating and deploying Docker images, creating and deploying operational scripts, and the final deployment of the model to the target. This pipeline could be triggered by new versions of an ML model.
We will have a deep dive into ML pipelining with Azure Machine Learning in Chapter 8, Azure Machine Learning Pipelines.
Having these pipelines, we can then turn our eye on Azure DevOps besides other tooling. With that, we can build a life cycle for our ML projects defined by the following parts:
- Creating or retraining a model: Here, we use training pipelines to create or retrain our model while version-controlling the pipelines and the code.
- Deploying the model and creating scoring files and dependencies: Here, we use a deployment pipeline to deploy a specific model version while version-controlling the pipeline and the code.
- Creating an audit trail: Through CI/CD pipelines and version control, we create an audit trail for all assets ensuring integrity and compliance.
- Monitoring model in production: We monitor the performance and possible data drift, which might automatically trigger retraining of the model.
We will discuss these topics and others in more detail in Chapter 16, Bringing Models into Production with MLOps.
This concludes our discussion on the end-to-end ML process and this chapter. If you hadn't already, you should now have a good understanding of ML and what to expect in the rest of the book.
Summary
In this chapter, we learned in which situations we should use ML and where it is coming from, we understood basic concepts of statistics and the mathematical knowledge we require for ML, and we discovered the steps we need to go through to create a performing ML model. In addition, we had a first glimpse at what is required to operationalize ML projects. This should give a base idea of what ML is about and what we will dive into in this book.
As this book not only covers ML but also the cloud platform Azure, in the next two chapters, we will go deeper into a topic that we have not covered so far—we will speak about tooling for ML. Therefore, in the next chapter, we will discover what Azure has to offer in the form of tools and services for ML, and in the third chapter, we will use the most useful tool to run our first hands-on experimentation with ML on Azure.




















 Download code from GitHub
Download code from GitHub
