Managing and Understanding Data
A key early component of any machine learning project involves managing and understanding data. Although this may not be as gratifying as building and deploying models—the stages in which you begin to see the fruits of your labor—it is unwise to ignore this important preparatory work.
Any learning algorithm is only as good as its training data, and in many cases, this data is complex, messy, and spread across multiple sources and formats. Due to this complexity, often the largest portion of effort invested in machine learning projects is spent on data preparation and exploration.
This chapter approaches data preparation in three ways. The first section discusses the basic data structures R uses to store data. You will become very familiar with these structures as you create and manipulate datasets. The second section is practical, as it covers several functions that are used for getting data in and out of R. In the third section, methods for understanding data are illustrated while exploring a real-world dataset.
By the end of this chapter, you will understand:
- How to use R’s basic data structures to store and manipulate values
- Simple functions to get data into R from common source formats
- Typical methods to understand and visualize complex data
The ways R handles data will dictate the ways you must work with data, so it is helpful to understand R’s data structures before jumping directly into data preparation. However, if you are already familiar with R programming, feel free to skip ahead to the section on data preprocessing.
All code files for this book can be found at https://github.com/PacktPublishing/Machine-Learning-with-R-Fourth-Edition
R data structures
There are numerous types of data structures found in programming languages, each with strengths and weaknesses suited to specific tasks. Since R is a programming language used widely for statistical data analysis, the data structures it utilizes were designed with this type of work in mind.
The R data structures used most frequently in machine learning are vectors, factors, lists, arrays, matrices, and data frames. Each is tailored to a specific data management task, which makes it important to understand how they will interact in your R project. In the sections that follow, we will review their similarities and differences.
Vectors
The fundamental R data structure is a vector, which stores an ordered set of values called elements. A vector can contain any number of elements. However, all of a vector’s elements must be of the same type; for instance, a vector cannot contain both numbers and text. To determine the type of vector v, use the typeof(v) command. Note that R is a case-sensitive language, which means that lower-case v and upper-case V could represent two different vectors. This is also true for R’s built-in functions and keywords, so be sure to always use the correct capitalization when typing R commands or expressions.
Several vector types are commonly used in machine learning: integer (numbers without decimals), double (numbers with decimals), character (text data, also commonly called “string” data), and logical (TRUE or FALSE values). Some R functions will report both integer and double vectors as numeric, while others distinguish between the two; generally, this distinction is unimportant. Vectors of logical values are used often in R, but notice that the TRUE and FALSE values must be written in all caps. This is slightly different from some other programming languages.
There are also two special values that are relevant to all vector types: NA, which indicates a missing value, and NULL, which is used to indicate the absence of any value. Although these two may seem to be synonymous, they are indeed slightly different. The NA value is a placeholder for something else and therefore has a length of one, while the NULL value is truly empty and has a length of zero.
It is tedious to enter large amounts of data by hand, but simple vectors can be created by using the c() combine function. The vector can also be given a name using the arrow <- operator. This is R’s assignment operator, used much like the = assignment operator used in many other programming languages.
R also allows the use of the = operator for assignment, but it is considered a poor coding style according to commonly accepted style guidelines.
For example, let’s construct a set of vectors containing data on three medical patients. We’ll create a character vector named subject_name to store the three patient names, a numeric vector named temperature to store each patient’s body temperature in degrees Fahrenheit, and a logical vector named flu_status to store each patient’s diagnosis (TRUE if they have influenza, FALSE otherwise). As shown in the following code, the three vectors are:
> subject_name <- c("John Doe", "Jane Doe", "Steve Graves")
> temperature <- c(98.1, 98.6, 101.4)
> flu_status <- c(FALSE, FALSE, TRUE)
Values stored in R vectors retain their order. Therefore, data for each patient can be accessed using their position in the set, beginning at 1, then supplying this number inside square brackets (that is, [ and ]) following the name of the vector. For instance, to obtain the temperature value for patient Jane Doe, the second patient, simply type:
> temperature[2]
[1] 98.6
R offers a variety of methods to extract data from vectors. A range of values can be obtained using the colon operator. For instance, to obtain the body temperature of the second and third patients, type:
> temperature[2:3]
[1] 98.6 101.4
Items can be excluded by specifying a negative item number. To exclude the second patient’s temperature data, type:
> temperature[-2]
[1] 98.1 101.4
It is also sometimes useful to specify a logical vector indicating whether each item should be included. For example, to include the first two temperature readings but exclude the third, type:
> temperature[c(TRUE, TRUE, FALSE)]
[1] 98.1 98.6
The importance of this type of operation is clearer with the realization that the result of a logical expression like temperature > 100 is a logical vector. This expression returns TRUE or FALSE depending on whether the temperature is greater than 100 degrees Fahrenheit, which indicates a fever. Therefore, the following commands will identify the patients exhibiting a fever:
> fever <- temperature > 100
> subject_name[fever]
[1] "Steve Graves"
Alternatively, the logical expression can also be moved inside the brackets, which returns the same result in a single step:
> subject_name[temperature > 100]
[1] "Steve Graves"
As you will see shortly, the vector provides the foundation for many other R data structures and can be combined with programming expressions to complete more complex operations for selecting data and constructing new features. Therefore, knowing the various vector operations is crucial for working with data in R.
Factors
Recall from Chapter 1, Introducing Machine Learning, that nominal features represent a characteristic with categories of values. Although it is possible to use a character vector to store nominal data, R provides a data structure specifically for this task.
A factor is a special type of vector that is solely used for representing categorical or ordinal data. In the medical dataset we are building, we might use a factor to represent the patients’ biological sex and record two categories: male and female.
Why use factors rather than character vectors? One advantage of factors is that the category labels are stored only once. Rather than storing MALE, MALE, FEMALE, the computer may store 1, 1, 2, which can reduce the memory needed to store the values. Additionally, many machine learning algorithms handle nominal and numeric features differently. Coding categorical features as factors allows R to treat the categorical features appropriately.
A factor should not be used for character vectors with values that don’t truly fall into categories. If a vector stores mostly unique values such as names or identification codes like social security numbers, keep it as a character vector.
To create a factor from a character vector, simply apply the factor() function. For example:
> gender <- factor(c("MALE", "FEMALE", "MALE"))
> gender
[1] MALE FEMALE MALE
Levels: FEMALE MALE
Notice that when the gender factor was displayed, R printed additional information about its levels. The levels comprise the set of possible categories the factor could take, in this case, MALE or FEMALE.
When we create factors, we can add additional levels that may not appear in the original data. Suppose we created another factor for blood type, as shown in the following example:
> blood <- factor(c("O", "AB", "A"),
levels = c("A", "B", "AB", "O"))
> blood
[1] O AB A
Levels: A B AB O
When we defined the blood factor, we specified an additional vector of four possible blood types using the levels parameter. As a result, even though our data includes only blood types O, AB, and A, all four types are retained with the blood factor, as the output shows. Storing the additional level allows for the possibility of adding patients with the other blood type in the future. It also ensures that if we were to create a table of blood types, we would know that type B exists, despite it not being found in our initial data.
The factor data structure also allows us to include information about the order of a nominal feature’s categories, which provides a method for creating ordinal features. For example, suppose we have data on the severity of patient symptoms, coded in increasing order of severity from mild, to moderate, to severe. We indicate the presence of ordinal data by providing the factor’s levels in the desired order, listed ascending from lowest to highest, and setting the ordered parameter to TRUE as shown:
> symptoms <- factor(c("SEVERE", "MILD", "MODERATE"),
levels = c("MILD", "MODERATE", "SEVERE"),
ordered = TRUE)
The resulting symptoms factor now includes information about the requested order. Unlike our prior factors, the levels of this factor are separated by < symbols to indicate the presence of a sequential order from MILD to SEVERE:
> symptoms
[1] SEVERE MILD MODERATE
Levels: MILD < MODERATE < SEVERE
A helpful feature of ordered factors is that logical tests work as you would expect. For instance, we can test whether each patient’s symptoms are more severe than moderate:
> symptoms > "MODERATE"
[1] TRUE FALSE FALSE
Machine learning algorithms capable of modeling ordinal data will expect ordered factors, so be sure to code your data accordingly.
Lists
A list is a data structure, much like a vector, in that it is used for storing an ordered set of elements. However, where a vector requires all its elements to be the same type, a list allows different R data types to be collected. Due to this flexibility, lists are often used to store various types of input and output data and sets of configuration parameters for machine learning models.
To illustrate lists, consider the medical patient dataset we have been constructing, with data for three patients stored in six vectors. If we wanted to display all the data for the first patient, we would need to enter five R commands:
> subject_name[1]
[1] "John Doe"
> temperature[1]
[1] 98.1
> flu_status[1]
[1] FALSE
> gender[1]
[1] MALE
Levels: FEMALE MALE
> blood[1]
[1] O
Levels: A B AB O
> symptoms[1]
[1] SEVERE
Levels: MILD < MODERATE < SEVERE
If we expect to examine the patient’s data again in the future, rather than retyping these commands, a list allows us to group all the values into one object we can use repeatedly.
Similar to creating a vector with c(), a list is created using the list() function, as shown in the following example. One notable difference is that when a list is constructed, each component in the sequence should be given a name. The names are not strictly required, but allow the values to be accessed later by name rather than by numbered position and a mess of square brackets. To create a list with named components for the first patient’s values, type the following:
> subject1 <- list(fullname = subject_name[1],
temperature = temperature[1],
flu_status = flu_status[1],
gender = gender[1],
blood = blood[1],
symptoms = symptoms[1])
This patient’s data is now collected in the subject1 list:
> subject1
$fullname
[1] "John Doe"
$temperature
[1] 98.1
$flu_status
[1] FALSE
$gender
[1] MALE
Levels: FEMALE MALE
$blood
[1] O
Levels: A B AB O
$symptoms
[1] SEVERE
Levels: MILD < MODERATE < SEVERE
Note that the values are labeled with the names we specified in the preceding command. As a list retains order like a vector, its components can be accessed using numeric positions, as shown here for the temperature value:
> subject1[2]
$temperature
[1] 98.1
The result of using vector-style operators on a list object is another list object, which is a subset of the original list. For example, the preceding code returned a list with a single temperature component. To instead return a single list item in its native data type, use double brackets ([[ and ]]) when selecting the list component. For example, the following command returns a numeric vector of length 1:
> subject1[[2]]
[1] 98.1
For clarity, it is often better to access list components by name, by appending a $ and the component name to the list name as follows:
> subject1$temperature
[1] 98.1
Like the double-bracket notation, this returns the list component in its native data type (in this case, a numeric vector of length 1).
Accessing the value by name also ensures that the correct item is retrieved even if the order of the list elements is changed later.
It is possible to obtain several list items by specifying a vector of names. The following returns a subset of the subject1 list, which contains only the temperature and flu_status components:
> subject1[c("temperature", "flu_status")]
$temperature
[1] 98.1
$flu_status
[1] FALSE
Entire datasets could be constructed using lists, and lists of lists. For example, you might consider creating a subject2 and subject3 list and grouping these into a list object named pt_data. However, constructing a dataset in this way is common enough that R provides a specialized data structure specifically for this task.
Data frames
By far the most important R data structure for machine learning is the data frame, a structure analogous to a spreadsheet or database in that it has both rows and columns of data. In R terms, a data frame can be understood as a list of vectors or factors, each having exactly the same number of values. Because the data frame is literally a list of vector-type objects, it combines aspects of both vectors and lists.
Let’s create a data frame for our patient dataset. Using the patient data vectors we created previously, the data.frame() function combines them into a data frame:
> pt_data <- data.frame(subject_name, temperature,
flu_status, gender, blood, symptoms)
When displaying the pt_data data frame, we see that the structure is quite different from the data structures we’ve worked with previously:
> pt_data
subject_name temperature flu_status gender blood symptoms
1 John Doe 98.1 FALSE MALE O SEVERE
2 Jane Doe 98.6 FALSE FEMALE AB MILD
3 Steve Graves 101.4 TRUE MALE A MODERATE
Compared to one-dimensional vectors, factors, and lists, a data frame has two dimensions and is displayed in a tabular format. Our data frame has one row for each patient and one column for each vector of patient measurements. In machine learning terms, the data frame’s rows are the examples, and the columns are the features or attributes.
To extract entire columns (vectors) of data, we can take advantage of the fact that a data frame is simply a list of vectors. Like lists, the most direct way to extract a single element is by referring to it by name. For example, to obtain the subject_name vector, type:
> pt_data$subject_name
[1] "John Doe" "Jane Doe" "Steve Graves"
Like lists, a vector of names can be used to extract multiple columns from a data frame:
> pt_data[c("temperature", "flu_status")]
temperature flu_status
1 98.1 FALSE
2 98.6 FALSE
3 101.4 TRUE
When we request data frame columns by name, the result is a data frame containing all rows of data for the specified columns. The command pt_data[2:3] will also extract the temperature and flu_status columns. However, referring to the columns by name results in clear and easy-to-maintain R code, which will not break if the data frame is later reordered.
To extract specific values from the data frame, methods like those for accessing values in vectors are used. However, there is an important distinction—because the data frame is two-dimensional, both the desired rows and columns must be specified. Rows are specified first, followed by a comma, followed by the columns in a format like this: [rows, columns]. As with vectors, rows and columns are counted beginning at one.
For instance, to extract the value in the first row and second column of the patient data frame, use the following command:
> pt_data[1, 2]
[1] 98.1
If you would like more than a single row or column of data, specify vectors indicating the desired rows and columns. The following statement will pull data from the first and third rows and the second and fourth columns:
> pt_data[c(1, 3), c(2, 4)]
temperature gender
1 98.1 MALE
3 101.4 MALE
To refer to every row or every column, simply leave the row or column portion blank. For example, to extract all rows of the first column:
> pt_data[, 1]
[1] "John Doe" "Jane Doe" "Steve Graves"
To extract all columns for the first row:
> pt_data[1, ]
subject_name temperature flu_status gender blood symptoms
1 John Doe 98.1 FALSE MALE O SEVERE
And to extract everything:
> pt_data[ , ]
subject_name temperature flu_status gender blood symptoms
1 John Doe 98.1 FALSE MALE O SEVERE
2 Jane Doe 98.6 FALSE FEMALE AB MILD
3 Steve Graves 101.4 TRUE MALE A MODERATE
Of course, columns are better accessed by name rather than position, and negative signs can be used to exclude rows or columns of data. Therefore, the output of the command:
> pt_data[c(1, 3), c("temperature", "gender")]
temperature gender
1 98.1 MALE
3 101.4 MALE
is equivalent to:
> pt_data[-2, c(-1, -3, -5, -6)]
temperature gender
1 98.1 MALE
3 101.4 MALE
We often need to create new columns in data frames—perhaps, for instance, as a function of existing columns. For example, we may need to convert the Fahrenheit temperature readings in the patient data frame into the Celsius scale. To do this, we simply use the assignment operator to assign the result of the conversion calculation to a new column name as follows:
> pt_data$temp_c <- (pt_data$temperature - 32) * (5 / 9)
To confirm the calculation worked, let’s compare the new Celsius-based temp_c column to the previous Fahrenheit-scale temperature column:
> pt_data[c("temperature", "temp_c")]
temperature temp_c
1 98.1 36.72222
2 98.6 37.00000
3 101.4 38.55556
Seeing these side by side, we can confirm that the calculation has worked correctly.
As these types of operations are crucial for much of the work we will do in upcoming chapters, it is important to become very familiar with data frames. You might try practicing similar operations with the patient dataset, or even better, use data from one of your own projects—the functions to load your own data files into R will be described later in this chapter.
Matrices and arrays
In addition to data frames, R provides other structures that store values in tabular form. A matrix is a data structure that represents a two-dimensional table with rows and columns of data. Like vectors, R matrices can contain only one type of data, although they are most often used for mathematical operations and therefore typically store only numbers.
To create a matrix, simply supply a vector of data to the matrix() function, along with a parameter specifying the number of rows (nrow) or number of columns (ncol). For example, to create a 2x2 matrix storing the numbers one to four, we can use the nrow parameter to request the data be divided into two rows:
> m <- matrix(c(1, 2, 3, 4), nrow = 2)
> m
[,1] [,2]
[1,] 1 3
[2,] 2 4
This is equivalent to the matrix produced using ncol = 2:
> m <- matrix(c(1, 2, 3, 4), ncol = 2)
> m
[,1] [,2]
[1,] 1 3
[2,] 2 4
You will notice that R loaded the first column of the matrix first before loading the second column. This is called column-major order, which is R’s default method for loading matrices.
To override this default setting and load a matrix by rows, set the parameter byrow = TRUE when creating the matrix.
To illustrate this further, let’s see what happens if we add more values to the matrix. With six values, requesting two rows creates a matrix with three columns:
> m <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 2)
> m
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
Requesting two columns creates a matrix with three rows:
> m <- matrix(c(1, 2, 3, 4, 5, 6), ncol = 2)
> m
[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
As with data frames, values in matrices can be extracted using [row, column] notation. For instance, m[1, 1] will return the value 1 while m[3, 2] will extract 6 from the m matrix. Additionally, entire rows or columns can be requested:
> m[1, ]
[1] 1 4
> m[, 1]
[1] 1 2 3
Closely related to the matrix structure is the array, which is a multidimensional table of data. Where a matrix has rows and columns of values, an array has rows, columns, and one or more additional layers of values. Although we will occasionally use matrices in later chapters, the use of arrays is unnecessary within the scope of this book.
Managing data with R
One of the challenges faced while working with massive datasets involves gathering, preparing, and otherwise managing data from a variety of sources. Although we will cover data preparation, data cleaning, and data management in depth by working on real-world machine learning tasks in later chapters, this section highlights the basic functionality for getting data in and out of R.
Saving, loading, and removing R data structures
When you’ve spent a lot of time getting a data frame into the desired form, you shouldn’t need to recreate your work each time you restart your R session.
To save data structures to a file that can be reloaded later or transferred to another system, the save() function can be used to write one or more R data structures to the location specified by the file parameter. R data files have an .RData or .rda extension.
Suppose you had three objects named x, y, and z that you would like to save to a permanent file. These might be vectors, factors, lists, data frames, or any other R object. To save them to a file named mydata.RData, use the following command:
> save(x, y, z, file = "mydata.RData")
The load() command can recreate any data structures that have been saved to an .RData file. To load the mydata.RData file created in the preceding code, simply type:
> load("mydata.RData")
This will recreate the x, y, and z data structures in your R environment.
Be careful what you are loading! All data structures stored in the file you are importing with the load() command will be added to your workspace, even if they overwrite something else you are working on.
Alternatively, the saveRDS() function can be used to save a single R object to a file. Although it is much like the save() function, a key distinction is that the corresponding loadRDS() function allows the object to be loaded with a different name to the original object. For this reason, saveRDS() may be safer to use when transferring R objects across projects, because it reduces the risk of accidentally overwriting existing objects in the R environment.
The saveRDS() function is especially helpful for saving machine learning model objects. Because some machine learning algorithms take a long time to train the model, saving the model to an .rds file can help avoid a long re-training process when a project is resumed. For example, to save a model object named my_model to a file named my_model.rds, use the following syntax:
> saveRDS(my_model, file = "my_model.rds")
To load the model, use the readRDS() function and assign the result an object name as follows:
> my_model <- readRDS("my_model.rds")
After you’ve been working in an R session for some time, you may have accumulated unused data structures. In RStudio, these objects are visible in the Environment tab of the interface, but it is also possible to access these objects programmatically using the listing function ls(), which returns a vector of all data structures currently in memory.
For example, if you’ve been following along with the code in this chapter, the ls() function returns the following:
> ls()
[1] "blood" "fever" "flu_status" "gender"
[5] "m" "pt_data" "subject_name" "subject1"
[9] "symptoms" "temperature"
R automatically clears all data structures from memory upon quitting the session, but for large objects, you may want to free up the memory sooner. The remove function rm() can be used for this purpose. For example, to eliminate the m and subject1 objects, simply type:
> rm(m, subject1)
The rm() function can also be supplied with a character vector of object names to remove. This works with the ls() function to clear the entire R session:
> rm(list = ls())
Be very careful when executing the preceding code, as you will not be prompted before your objects are removed!
If you need to wrap up your R session in a hurry, the save.image() command will write your entire session to a file simply called .RData. By default, when quitting R or RStudio, you will be asked if you would like to create this file. R will look for this file the next time you start R, and if it exists, your session will be recreated just as you had left it.
Importing and saving datasets from CSV files
It is common for public datasets to be stored in text files. Text files can be read on virtually any computer or operating system, which makes the format nearly universal. They can also be exported and imported from and to programs such as Microsoft Excel, providing a quick and easy way to work with spreadsheet data.
A tabular (as in “table”) data file is structured in matrix form, such that each line of text reflects one example, and each example has the same number of features. The feature values on each line are separated by a predefined symbol known as a delimiter. Often, the first line of a tabular data file lists the names of the data columns. This is called a header line.
Perhaps the most common tabular text file format is the comma-separated values (CSV) file, which, as the name suggests, uses the comma as a delimiter. CSV files can be imported to and exported from many common applications. A CSV file representing the medical dataset constructed previously could be stored as:
subject_name,temperature,flu_status,gender,blood_type
John Doe,98.1,FALSE,MALE,O
Jane Doe,98.6,FALSE,FEMALE,AB
Steve Graves,101.4,TRUE,MALE,A
Given a patient data file named pt_data.csv located in the R working directory, the read.csv() function can be used as follows to load the file into R:
> pt_data <- read.csv("pt_data.csv")
This will read the CSV file into a data frame titled pt_data. If your dataset resides outside the R working directory, the full path to the CSV file (for example, "/path/to/mydata.csv") can be used when calling the read.csv() function.
By default, R assumes that the CSV file includes a header line listing the names of the features in the dataset. If a CSV file does not have a header, specify the option header = FALSE as shown in the following command, and R will assign generic feature names by numbering the columns sequentially as V1, V2, and so on:
> pt_data <- read.csv("pt_data.csv", header = FALSE)
As an important historical note, in versions of R prior to 4.0, the read.csv() function automatically converted all character type columns into factors due to a stringsAsFactors parameter that was set to TRUE by default. This feature was occasionally helpful, especially on the smaller and simpler datasets used in the earlier years of R. However, as datasets have become larger and more complex, this feature began to cause more problems than it solved. Now, starting with version 4.0, R sets stringsAsFactors = FALSE by default. If you are certain that every character column in a CSV file is truly a factor, it is possible to convert them using the following syntax:
> pt_data <- read.csv("pt_data.csv", stringsAsFactors = TRUE)
We will set stringsAsFactors = TRUE occasionally throughout the book, when working with datasets in which all character columns are truly factors.
Getting results data out of R can be almost as important as getting it in! To save a data frame to a CSV file, use the write.csv() function. For a data frame named pt_data, simply enter:
> write.csv(pt_data, file = "pt_data.csv", row.names = FALSE)
This will write a CSV file with the name pt_data.csv to the R working folder. The row.names parameter overrides R’s default setting, which is to output row names in the CSV file. Generally, this output is unnecessary and will simply inflate the size of the resulting file.
For more sophisticated control over reading in files, note that read.csv() is a special case of the read.table() function, which can read tabular data in many different forms. This includes other delimited formats such as tab-separated values (TSV) and vertical bar (|) delimited files. For more detailed information on the read.table() family of functions, refer to the R help page using the ?read.table command.
Importing common dataset formats using RStudio
For more complex importation scenarios, the RStudio Desktop software offers a simple interface, which will guide you through the process of writing R code that can be used to load the data into your project. Although it has always been relatively easy to load plaintext data formats like CSV, importing other common analytical data formats like Microsoft Excel (.xls and .xlsx), SAS (.sas7bdat and .xpt), SPSS (.sav and .por), and Stata (.dta) was once a tedious and time-consuming process, requiring knowledge of specific tricks and tools across multiple R packages. Now, the functionality is available via the Import Dataset command near the upper right of the RStudio interface, as shown in Figure 2.1:

Figure 2.1: RStudio’s “Import Dataset” feature provides options to load data from a variety of common formats
Depending on the data format selected, you may be prompted to install R packages that are required for the functionality in question. Behind the scenes, these packages will translate the data format so that it can be used in R. You will then be presented with a dialog box allowing you to choose the options for the data import process and see a live preview of how the data will appear in R as these changes are made.
The following screenshot illustrates the process of importing a Microsoft Excel version of the used cars dataset using the readxl package (https://readxl.tidyverse.org), but the process is similar for any of the dataset formats:

Figure 2.2: The data import dialog provides a “Code Preview” that can be copy-and-pasted into your R code file
The Code Preview in the bottom-right of this dialog provides the R code to perform the importation with the specified options. Selecting the Import button will immediately execute the code; however, a better practice is to copy and paste the code into your R source code file, so that you can re-import the dataset in future sessions.
The read_excel() function RStudio uses to load Excel data creates an R object called a “tibble” rather than a data frame. The differences are so subtle that you may not even notice! However, tibbles are an important R innovation enabling new ways to work with data frames. The tibble and its functionality are discussed in Chapter 12, Advanced Data Preparation.
The RStudio interface has made it easier than ever to work with data in a variety of formats, but more advanced functionality exists for working with large datasets. In particular, if you have data residing in database platforms like Microsoft SQL, MySQL, PostgreSQL, and others, it is possible to connect R to such databases to pull the data into R, or even utilize the database hardware itself to perform big data computations prior to bringing the results into R. Chapter 15, Making Use of Big Data, introduces these techniques and provides instructions for connecting to common databases using RStudio.
Exploring and understanding data
After collecting data and loading it into R data structures, the next step in the machine learning process involves examining the data in detail. It is during this step that you will begin to explore the data’s features and examples and realize the peculiarities that make your data unique. The better you understand your data, the better you will be able to match a machine learning model to your learning problem.
The best way to learn the process of data exploration is by example. In this section, we will explore the usedcars.csv dataset, which contains actual data about used cars advertised for sale on a popular US website in the year 2012.
The usedcars.csv dataset is available for download on the Packt Publishing support page for this book. If you are following along with the examples, be sure that this file has been downloaded and saved to your R working directory.
Since the dataset is stored in CSV form, we can use the read.csv() function to load the data into an R data frame:
> usedcars <- read.csv("usedcars.csv")
Using the usedcars data frame, we will now assume the role of a data scientist who has the task of understanding the used car data. Although data exploration is a fluid process, the steps can be imagined as a sort of investigation in which questions about the data are answered. The exact questions may vary across projects, but the types of questions are always similar.
You should be able to adapt the basic steps of this investigation to any dataset you like, whether large or small.

Figure 2.3: “Do pricing algorithms get a test drive?” (image created by Midjourney AI with the prompt of “cute cartoon robot buying a used car”)
Exploring the structure of data
The first questions to ask in an investigation of a new dataset should be about how the dataset is organized. If you are fortunate, your source will provide a data dictionary, a document that describes the dataset’s features. In our case, the used car data does not come with this documentation, so we’ll need to create our own.
The str() function provides a method for displaying the structure of R objects, such as data frames, vectors, or lists. It can be used to create the basic outline for our data dictionary:
> str(usedcars)
'data.frame': 150 obs. of 6 variables:
$ year : int 2011 2011 2011 2011 ...
$ model : chr "SEL" "SEL" "SEL" "SEL" ...
$ price : int 21992 20995 19995 17809 ...
$ mileage : int 7413 10926 7351 11613 ...
$ color : chr "Yellow" "Gray" "Silver" "Gray" ...
$ transmission: chr "AUTO" "AUTO" "AUTO" "AUTO" ...
For such a simple command, we learn a wealth of information about the dataset. The statement 150 obs informs us that the data includes 150 observations, which is just another way of saying that the dataset contains 150 rows or examples. The number of observations is often simply abbreviated as n.
Since we know that the data describes used cars, we can now presume that we have examples of n = 150 automobiles for sale.
The 6 variables statement refers to the six features that were recorded in the data. The term variable is borrowed from the field of statistics, and simply means a mathematical object that can take various values—like the x and y variables you might solve for in an algebraic equation. These features, or variables, are listed by name on separate lines. Looking at the line for the feature called color, we note some additional details:
$ color : chr "Yellow" "Gray" "Silver" "Gray" ...
After the variable’s name, the chr label tells us that the feature is the character type. In this dataset, three of the variables are character while three are noted as int, which refers to the integer type. Although the usedcars dataset includes only character and integer features, you are also likely to encounter num, or numeric type, when using non-integer data. Any factors would be listed as the factor type. Following each variable’s type, R presents a sequence of the first few feature values. The values "Yellow" "Gray" "Silver" "Gray" are the first four values of the color feature.
Applying a bit of subject-area knowledge to the feature names and values allows us to make some assumptions about what the features represent. year could refer to the year the vehicle was manufactured, or it could specify the year the advertisement was posted. We’ll have to investigate this feature later in more detail, since the four example values (2011 2011 2011 2011) could be used to argue for either possibility. The model, price, mileage, color, and transmission most likely refer to the characteristics of the car for sale.
Although our data appears to have been given meaningful names, this is not always the case. Sometimes datasets have features with nonsensical names or codes, like V1. In these cases, it may be necessary to do additional sleuthing to determine what a feature represents. Still, even with helpful feature names, it is always prudent to be skeptical about the provided labels. Let’s investigate further.
Exploring numeric features
To investigate the numeric features in the used car data, we will employ a common set of measurements for describing values known as summary statistics. The summary() function displays several common summary statistics. Let’s look at a single feature, year:
> summary(usedcars$year)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2000 2008 2009 2009 2010 2012
Ignoring the meaning of the values for now, the fact that we see numbers such as 2000, 2008, and 2009 leads us to believe that year indicates the year of manufacture rather than the year the advertisement was posted, since we know the vehicle listings were obtained in 2012.
By supplying a vector of column names, we can also use the summary() function to obtain summary statistics for several numeric columns at the same time:
> summary(usedcars[c("price", "mileage")])
price mileage
Min. : 3800 Min. : 4867
1st Qu.:10995 1st Qu.: 27200
Median :13592 Median : 36385
Mean :12962 Mean : 44261
3rd Qu.:14904 3rd Qu.: 55124
Max. :21992 Max. :151479
The six summary statistics provided by the summary() function are simple, yet powerful tools for investigating data. They can be divided into two types: measures of center and measures of spread.
Measuring the central tendency – mean and median
Measures of central tendency are a class of statistics used to identify a value that falls in the middle of a set of data. You are most likely already familiar with one common measure of center: the average. In common use, when something is deemed average, it falls somewhere between the extreme ends of the scale. An average student might have marks falling in the middle of their classmates’. An average weight is neither unusually light nor heavy. In general, an average item is typical and not too unlike the others in its group. You might think of it as an exemplar by which all the others are judged.
In statistics, the average is also known as the mean, which is a measurement defined as the sum of all values divided by the number of values. For example, to calculate the mean income in a group of three people with incomes of $36,000, $44,000, and $56,000, we could type:
> (36000 + 44000 + 56000) / 3
[1] 45333.33
R also provides a mean() function, which calculates the mean for a vector of numbers:
> mean(c(36000, 44000, 56000))
[1] 45333.33
The mean income of this group of people is about $45,333. Conceptually, this can be imagined as the income each person would have if the total income was divided equally across every person.
Recall that the preceding summary() output listed mean values for price and mileage. These values suggest that the typical used car in this dataset was listed at a price of $12,962 and had an odometer reading of 44,261. What does this tell us about our data? We can note that because the average price is relatively low, we might expect that the dataset contains economy-class cars. Of course, the data could also include late-model luxury cars with high mileage, but the relatively low mean mileage statistic doesn’t provide evidence to support this hypothesis. On the other hand, it doesn’t provide evidence to ignore the possibility either. We’ll need to keep this in mind as we examine the data further.
Although the mean is by far the most cited statistic for measuring the center of a dataset, it is not always the most appropriate one. Another commonly used measure of central tendency is the median, which is the value that occurs at the midpoint of an ordered list of values. As with the mean, R provides a median() function, which we can apply to our salary data as shown in the following example:
> median(c(36000, 44000, 56000))
[1] 44000
So, because the middle value is 44000, the median income is $44,000.
If a dataset has an even number of values, there is no middle value. In this case, the median is commonly calculated as the average of the two values at the center of the ordered list. For example, the median of the values 1, 2, 3, and 4 is 2.5.
At first glance, it seems like the median and mean are very similar measures. Certainly, the mean value of $45,333 and the median value of $44,000 are not very far apart. Why have two measures of central tendency? The reason relates to the fact that the mean and median are affected differently by values falling at the far ends of the range. In particular, the mean is highly sensitive to outliers, or values that are atypically high or low relative to the majority of data. A more nuanced take on outliers will be presented in Chapter 11, Being Successful with Machine Learning, but for now, we can consider them extreme values that tend to shift the mean higher or lower relative to the median, because the median is largely insensitive to the outlying values.
Recall again the reported median values in the summary() output for the used car dataset. Although the mean and median for price are similar (differing by approximately five percent), there is a much larger difference between the mean and median for mileage. For mileage, the mean of 44,261 is more than 20 percent larger than the median of 36,385. Since the mean is more sensitive to extreme values than the median, the fact that the mean is much higher than the median might lead us to suspect that there are some used cars with extremely high mileage values relative to the others in the dataset. To investigate this further, we’ll need to add additional summary statistics to our analysis.
Measuring spread – quartiles and the five-number summary
The mean and median provide ways to quickly summarize values, but these measures of center tell us little about whether there is diversity in the measurements. To measure the diversity, we need to employ another type of summary statistics concerned with the spread of the data, or how tightly or loosely the values are spaced. Knowing about the spread provides a sense of the data’s highs and lows, and whether most values are like or unlike the mean and median.
The five-number summary is a set of five statistics that roughly depict the spread of a feature’s values. All five statistics are included in the summary() function output. Written in order, they are:
- Minimum (
Min.) - First quartile, or Q1 (
1st Qu.) - Median, or Q2 (
Median) - Third quartile, or Q3 (
3rd Qu.) - Maximum (
Max.)
As you would expect, the minimum and maximum are the most extreme feature values, indicating the smallest and largest values respectively. R provides the min() and max() functions to calculate these for a vector.
The span between the minimum and maximum value is known as the range. In R, the range() function returns both the minimum and maximum value:
> range(usedcars$price)
[1] 3800 21992
Combining range() with the difference function diff() allows you to compute the range statistic with a single line of code:
> diff(range(usedcars$price))
[1] 18192
One quarter of the dataset’s values fall below the first quartile (Q1), and another quarter is above the third quartile (Q3). Along with the median, which is the midpoint of the data values, the quartiles divide a dataset into four portions, each containing 25 percent of the values.
Quartiles are a special case of a type of statistic called quantiles, which are numbers that divide data into equally sized quantities. In addition to quartiles, commonly used quantiles include tertiles (three parts), quintiles (five parts), deciles (10 parts), and percentiles (100 parts). Percentiles are often used to describe the ranking of a value; for instance, a student whose test score was ranked at the 99th percentile performed better than or equal to 99 percent of the other test takers.
The middle 50 percent of data, found between the first and third quartiles, is of particular interest because it is a simple measure of spread. The difference between Q1 and Q3 is known as the interquartile range (IQR), and can be calculated with the IQR() function:
> IQR(usedcars$price)
[1] 3909.5
We could have also calculated this value by hand from the summary() output for the usedcars$price vector by computing 14904 – 10995 = 3909. The small difference between our calculation and the IQR() output is due to the fact that R automatically rounds the summary() output.
The quantile() function provides a versatile tool for identifying quantiles for a set of values. By default, quantile() returns the five-number summary. Applying the function to the usedcars$price vector results in the same summary statistics as before:
> quantile(usedcars$price)
0% 25% 50% 75% 100%
3800.0 10995.0 13591.5 14904.5 21992.0
When computing quantiles, there are many methods for handling ties among sets of values with no single middle value. The quantile() function allows you to specify among nine different tie-breaking algorithms by specifying the type parameter. If your project requires a precisely defined quantile, it is important to read the function documentation using the ?quantile command.
By supplying an additional probs parameter for a vector denoting cut points, we can obtain arbitrary quantiles, such as the 1st and 99th percentiles:
> quantile(usedcars$price, probs = c(0.01, 0.99))
1% 99%
5428.69 20505.00
The sequence function seq() generates vectors of evenly spaced values. This makes it easy to obtain other slices of data, such as the quintiles (five groups) shown in the following command:
> quantile(usedcars$price, seq(from = 0, to = 1, by = 0.20))
0% 20% 40% 60% 80% 100%
3800.0 10759.4 12993.8 13992.0 14999.0 21992.0
Equipped with an understanding of the five-number summary, we can re-examine the used car summary() output. For price, the minimum was $3,800 and the maximum was $21,992. Interestingly, the difference between the minimum and Q1 is about $7,000, as is the difference between Q3 and the maximum; yet, the difference from Q1 to the median to Q3 is roughly $2,000. This suggests that the lower and upper 25 percent of values are more widely dispersed than the middle 50 percent of values, which seem to be more tightly grouped around the center. We also see a similar trend with mileage. As you will learn later in this chapter, this pattern of spread is common enough that it has been called a “normal” distribution of data.
The spread of mileage also exhibits another interesting property—the difference between Q3 and the maximum is far greater than that between the minimum and Q1. In other words, the larger values are far more spread out than the smaller values. This finding helps explain why the mean value is much greater than the median. Because the mean is sensitive to extreme values, it is pulled higher, while the median stays in relatively the same place. This is an important property, which becomes more apparent when the data is presented visually.
Visualizing numeric features – boxplots
Visualizing numeric features can help diagnose data problems that might negatively affect machine learning model performance. A common visualization of the five-number summary is a boxplot, also known as a box-and-whisker plot. The boxplot displays the center and spread of a numeric variable in a format that allows you to quickly obtain a sense of its range and skew or compare it to other features.
Let’s look at a boxplot for the used car price and mileage data. To obtain a boxplot for a numeric vector, we will use the boxplot() function. We will also specify a pair of extra parameters, main and ylab, to add a title to the figure and label the y axis (the vertical axis), respectively. The commands to create the price and mileage boxplots are:
> boxplot(usedcars$price, main = "Boxplot of Used Car Prices",
ylab = "Price ($)")
> boxplot(usedcars$mileage, main = "Boxplot of Used Car Mileage",
ylab = "Odometer (mi.)")
R will produce figures as follows:
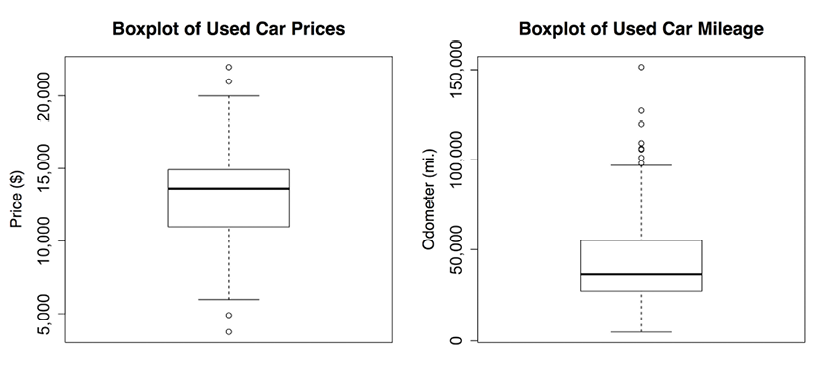
Figure 2.4: Boxplots of used car price and mileage data
A boxplot depicts the five-number summary using horizontal lines and dots. The horizontal lines forming the box in the middle of each figure represent Q1, Q2 (the median), and Q3 when reading the plot from bottom to top. The median is denoted by the dark line, which lines up with $13,592 on the vertical axis for price and 36,385 mi. on the vertical axis for mileage.
In simple boxplots, such as those in the preceding diagram, the box width is arbitrary and does not illustrate any characteristic of the data. For more sophisticated analyses, it is possible to use the shape and size of the boxes to facilitate comparisons of the data across several groups. To learn more about such features, begin by examining the notch and varwidth options in the R boxplot() documentation by typing the ?boxplot command.
The minimum and maximum values can be illustrated using whiskers that extend below and above the box; however, a widely used convention only allows the whiskers to extend to a minimum or maximum of 1.5 times the IQR below Q1 or above Q3. Any values that fall beyond this threshold are considered outliers and are denoted as circles or dots. For example, recall that the IQR for price was 3,909 with Q1 of 10,995 and Q3 of 14,904. An outlier is therefore any value that is less than 10995 - 1.5 * 3909 = 5131.5 or greater than 14904 + 1.5 * 3909 = 20767.5.
The price boxplot shows two outliers on both the high and low ends. On the mileage boxplot, there are no outliers on the low end and thus the bottom whisker extends to the minimum value of 4,867. On the high end, we see several outliers beyond the 100,000-mile mark. These outliers are responsible for our earlier finding, which noted that the mean value was much greater than the median.
Visualizing numeric features – histograms
A histogram is another way to visualize the spread of a numeric feature. It is like a boxplot in that it divides the feature values into a predefined number of portions or bins, which act as containers for values. Their similarities end there, however. Where a boxplot creates four portions containing the same number of values but varying in range, a histogram uses a larger number of portions of identical range and allows the bins to contain different numbers of values.
We can create a histogram for the used car price and mileage data using the hist() function. As we did with the boxplot, we will specify a title for the figure using the main parameter and label the x axis with the xlab parameter. The commands to create the histograms are:
> hist(usedcars$price, main = "Histogram of Used Car Prices",
xlab = "Price ($)")
> hist(usedcars$mileage, main = "Histogram of Used Car Mileage",
xlab = "Odometer (mi.)")
This produces the following diagrams:
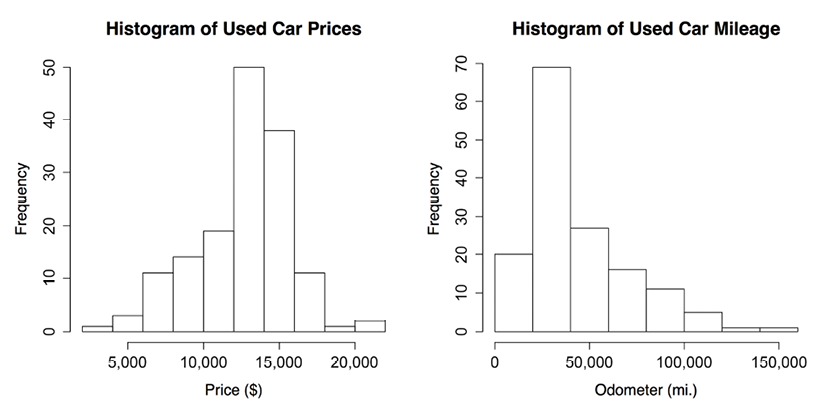
Figure 2.5: Histograms of used car price and mileage data
The histogram is composed of a series of bars with heights indicating the count, or frequency, of values falling within each of the equal-width bins partitioning the values. The vertical lines that separate the bars, as labeled on the horizontal axis, indicate the start and end points of the range of values falling within the bin.
You may have noticed that the preceding histograms have differing numbers of bins. This is because the hist() function attempts to identify the optimal number of bins for the feature’s range. If you’d like to override this default, use the breaks parameter. Supplying an integer such as breaks = 10 creates exactly 10 bins of equal width, while supplying a vector such as c(5000, 10000, 15000, 20000) creates bins that break at the specified values.
On the price histogram, each of the 10 bars spans an interval of $2,000, beginning at $2,000 and ending at $22,000. The tallest bar in the center of the figure covers the range from $12,000 to $14,000 and has a frequency of 50. Since we know our data includes 150 cars, we know that one-third of all the cars are priced from $12,000 to $14,000. Nearly 90 cars—more than half—are priced from $12,000 to $16,000.
The mileage histogram includes eight bars representing bins of 20,000 miles each, beginning at 0 and ending at 160,000 miles. Unlike the price histogram, the tallest bar is not in the center of the data, but on the left-hand side of the diagram. The 70 cars contained in this bin have odometer readings from 20,000 to 40,000 miles.
You might also notice that the shape of the two histograms is somewhat different. It seems that the used car prices tend to be evenly divided on both sides of the middle, while the car mileages stretch further to the right.
This characteristic is known as skew, or more specifically right skew, because the values on the high end (right side) are far more spread out than the values on the low end (left side). As shown in the following diagram, histograms of skewed data look stretched on one of the sides:

Figure 2.6: Three skew patterns visualized with idealized histograms
The ability to quickly diagnose such patterns in our data is one of the strengths of the histogram as a data exploration tool. This will become even more important as we start examining other patterns of spread in numeric data.
Understanding numeric data – uniform and normal distributions
Histograms, boxplots, and statistics describing the center and spread provide ways to examine the distribution of a feature’s values. A variable’s distribution describes how likely a value is to fall within various ranges.
If all values are equally likely to occur—say, for instance, in a dataset recording the values rolled on a fair six-sided die—the distribution is said to be uniform. A uniform distribution is easy to detect with a histogram because the bars are approximately the same height. The histogram may look something like the following diagram:

Figure 2.7: A uniform distribution visualized with an idealized histogram
It’s important to note that not all random events are uniform. For instance, rolling a weighted six-sided trick die would result in some numbers coming up more often than others. While each roll of the die results in a randomly selected number, they are not equally likely.
The used car price and mileage data are also clearly not uniform, since some values are seemingly far more likely to occur than others. In fact, on the price histogram, it seems that values become less likely to occur as they are further away from both sides of the center bar, which results in a bell-shaped distribution of data. This characteristic is so common in real-world data that it is the hallmark of the so-called normal distribution. The stereotypical bell-shaped curve of the normal distribution is shown in the following diagram:
Figure 2.8: A normal distribution visualized with an idealized histogram
Although there are numerous types of non-normal distributions, many real-world phenomena generate data that can be described by the normal distribution. Therefore, the normal distribution’s properties have been studied in detail.
Measuring spread – variance and standard deviation
Distributions allow us to characterize a large number of values using a smaller number of parameters. The normal distribution, which describes many types of real-world data, can be defined with just two: center and spread. The center of the normal distribution is defined by its mean value, which we have used before. The spread is measured by a statistic called the standard deviation.
To calculate the standard deviation, we must first obtain the variance, which is defined as the average of the squared differences between each value and the mean value. In mathematical notation, the variance of a set of n values in a set named x is defined by the following formula:

In this formula, the Greek letter mu (written as  ) denotes the mean of the values, and the variance itself is denoted by the Greek letter sigma squared (written as
) denotes the mean of the values, and the variance itself is denoted by the Greek letter sigma squared (written as  ).
).
The standard deviation is the square root of the variance, and is denoted by sigma (written as  ) as shown in the following formula:
) as shown in the following formula:

In R, the var() and sd() functions save us the trouble of calculating the variance and standard deviation by hand. For example, computing the variance and standard deviation of the price and mileage vectors, we find:
> var(usedcars$price)
[1] 9749892
> sd(usedcars$price)
[1] 3122.482
> var(usedcars$mileage)
[1] 728033954
> sd(usedcars$mileage)
[1] 26982.1
When interpreting the variance, larger numbers indicate that the data is spread more widely around the mean. The standard deviation indicates, on average, how much each value differs from the mean.
If you compute these statistics by hand using the formulas in the preceding diagrams, you will obtain a slightly different result than the built-in R functions. This is because the preceding formulas use the population variance (which divides by n), while R uses the sample variance (which divides by n - 1). Except for very small datasets, the distinction is minor.
The standard deviation can be used to quickly estimate how extreme a given value is under the assumption that it came from a normal distribution. The 68–95–99.7 rule states that 68 percent of values in a normal distribution fall within one standard deviation of the mean, while 95 percent and 99.7 percent of values fall within two and three standard deviations, respectively. This is illustrated in the following diagram:
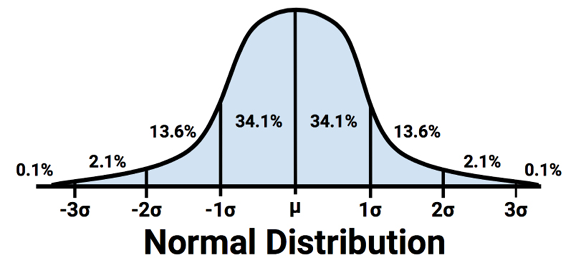
Figure 2.9: The percent of values within one, two, and three standard deviations of a normal distribution’s mean
Applying this information to the used car data, we know that the mean and standard deviation of price were $12,962 and $3,122 respectively. Therefore, by assuming that the prices are normally distributed, approximately 68 percent of cars in our data were advertised at prices between $12,962 - $3,122 = $9,840 and $12,962 + $3,122 = $16,804.
Although, strictly speaking, the 68–95–99.7 rule only applies to normal distributions, the basic principle applies to almost any data; values more than three standard deviations away from the mean tend to be exceedingly rare events.
Exploring categorical features
If you recall, the used car dataset contains three categorical features: model, color, and transmission. Additionally, although year is stored as a numeric vector, each year can be imagined as a category applying to multiple cars. We might therefore consider treating it as categorical as well.
In contrast to numeric data, categorical data is typically examined using tables rather than summary statistics. A table that presents a single categorical feature is known as a one-way table. The table() function can be used to generate one-way tables for the used car data:
> table(usedcars$year)
2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012
3 1 1 1 3 2 6 11 14 42 49 16 1
> table(usedcars$model)
SE SEL SES
78 23 49
> table(usedcars$color)
Black Blue Gold Gray Green Red Silver White Yellow
35 17 1 16 5 25 32 16 3
The table() output lists the categories of the nominal variable and a count of the number of values falling into each category. Since we know there are 150 used cars in the dataset, we can determine that roughly one-third of all the cars were manufactured in 2010, given that 49/150 = 0.327.
R can also perform the calculation of table proportions directly, by using the prop.table() command on a table produced by the table() function:
> model_table <- table(usedcars$model)
> prop.table(model_table)
SE SEL SES
0.5200000 0.1533333 0.3266667
The results of prop.table() can be combined with other R functions to transform the output. Suppose we would like to display the results in percentages with a single decimal place. We can do this by multiplying the proportions by 100, then using the round() function while specifying digits = 1, as shown in the following example:
> color_table <- table(usedcars$color)
> color_pct <- prop.table(color_table) * 100
> round(color_pct, digits = 1)
Black Blue Gold Gray Green Red Silver White Yellow
23.3 11.3 0.7 10.7 3.3 16.7 21.3 10.7 2.0
Although this includes the same information as the default prop.table() output, the changes make it easier to read. The results show that black is the most common color, with nearly a quarter (23.3 percent) of all advertised cars. Silver is a close second with 21.3 percent, and red is third with 16.7 percent.
Measuring the central tendency – the mode
In statistics terminology, the mode of a feature is the value occurring most often. Like the mean and median, the mode is another measure of central tendency. It is typically used for categorical data, since the mean and median are not defined for nominal variables.
For example, in the used car data, the mode of year is 2010, while the modes for the model and color variables are SE and Black, respectively. A variable may have more than one mode; a variable with a single mode is unimodal, while a variable with two modes is bimodal. Data with multiple modes is more generally called multimodal.
Although you might suspect that you could use the mode() function, R uses this to obtain the type of variable (as in numeric, list, and so on) rather than the statistical mode. Instead, to find the statistical mode, simply look at the table() output for the category with the greatest number of values.
The mode or modes are used in a qualitative sense to gain an understanding of important values. Even so, it would be dangerous to place too much emphasis on the mode since the most common value is not necessarily a majority. For instance, although black was the single most common car color, it was only about a quarter of all advertised cars.
It is best to think about the modes in relation to the other categories. Is there one category that dominates all others, or are there several? Thinking about modes this way may help to generate testable hypotheses by raising questions about what makes certain values more common than others. If black and silver are common used car colors, we might believe that the data represents luxury cars, which tend to be sold in more conservative colors. Alternatively, these colors could indicate economy cars, which are sold with fewer color options. We will keep these questions in mind as we continue to examine this data.
Thinking about the modes as common values allows us to apply the concept of the statistical mode to numeric data. Strictly speaking, it would be unlikely to have a mode for a continuous variable, since no two values are likely to repeat. However, if we think about modes as the highest bars on a histogram, we can discuss the modes of variables such as price and mileage. It can be helpful to consider the mode when exploring numeric data, particularly to examine whether the data is multimodal.

Figure 2.10: Hypothetical distributions of numeric data with one and two modes
Exploring relationships between features
So far, we have examined variables one at a time, calculating only univariate statistics. During our investigation, we raised questions that we were unable to answer before:
- Does the
priceandmileagedata imply that we are examining only economy-class cars, or are there luxury cars with high mileage? - Do relationships between
modelandcolorprovide insight into the types of cars we are examining?
These types of questions can be addressed by looking at bivariate relationships, which consider the relationship between two variables. Relationships of more than two variables are called multivariate relationships. Let’s begin with the bivariate case.
Visualizing relationships – scatterplots
A scatterplot is a diagram that visualizes a bivariate relationship between numeric features. It is a two-dimensional figure in which dots are drawn on a coordinate plane using the values of one feature to provide the horizontal x coordinates, and the values of another feature to provide the vertical y coordinates. Patterns in the placement of dots reveal underlying associations between the two features.
To answer our question about the relationship between price and mileage, we will examine a scatterplot. We’ll use the plot() function, along with the main, xlab, and ylab parameters used previously to label the diagram.
To use plot(), we need to specify x and y vectors containing the values used to position the dots on the figure. Although the conclusions would be the same regardless of the variable used to supply the x and y coordinates, convention dictates that the y variable is the one that is presumed to depend on the other (and is therefore known as the dependent variable). Since a seller cannot modify a car’s odometer reading, mileage is unlikely to be dependent on the car’s price. Instead, our hypothesis is that a car’s price depends on the odometer mileage. Therefore, we will select price as the dependent y variable.
The full command to create our scatterplot is:
> plot(x = usedcars$mileage, y = usedcars$price,
main = "Scatterplot of Price vs. Mileage",
xlab = "Used Car Odometer (mi.)",
ylab = "Used Car Price ($)")
This produces the following scatterplot:
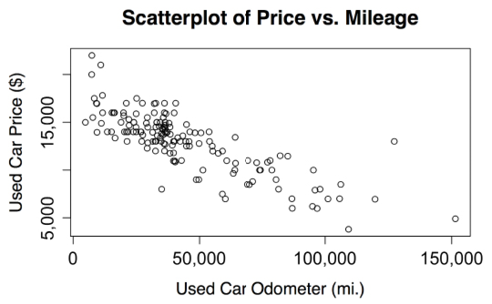
Figure 2.11: The relationship between used car price and mileage
Using the scatterplot, we notice a clear relationship between the price of a used car and the odometer reading. To read the plot, examine how the values of the y axis variable change as the values on the x axis increase. In this case, car prices tend to be lower as the mileage increases. If you have ever sold or shopped for a used car, this is not a profound insight.
Perhaps a more interesting finding is the fact that there are very few cars that have both high price and high mileage, aside from a lone outlier at about 125,000 miles and $14,000. The absence of more points like this provides evidence to support the conclusion that our dataset is unlikely to include any high-mileage luxury cars. All the most expensive cars in the data, particularly those above $17,500, seem to have extraordinarily low mileage, which implies that we could be looking at a single type of car that retails for a price of around $20,000 when new.
The relationship we’ve observed between car prices and mileage is known as a negative association because it forms a pattern of dots in a line sloping downward. A positive association would appear to form a line sloping upward. A flat line, or a seemingly random scattering of dots, is evidence that the two variables are not associated at all. The strength of a linear association between two variables is measured by a statistic known as correlation. Correlations are discussed in detail in Chapter 6, Forecasting Numeric Data – Regression Methods, which covers methods for modeling linear relationships.
Keep in mind that not all associations form straight lines. Sometimes the dots form a U shape or V shape, while sometimes the pattern seems to be weaker or stronger for increasing values of the x or y variable. Such patterns imply that the relationship between the two variables is not linear, and thus correlation would be a poor measure of their association.
Examining relationships – two-way cross-tabulations
To examine a relationship between two nominal variables, a two-way cross-tabulation is used (also known as a crosstab or contingency table). A cross-tabulation is like a scatterplot in that it allows you to examine how the values of one variable vary by the values of another. The format is a table in which the rows are the levels of one variable, while the columns are the levels of another. Counts in each of the table’s cells indicate the number of values falling into the row and column combination.
To answer our earlier question about whether there is a relationship between model and color, we will examine a crosstab. There are several functions to produce two-way tables in R, including table(), which we used before for one-way tables. The CrossTable() function in the gmodels package by Gregory R. Warnes is perhaps the most user-friendly, as it presents the row, column, and margin percentages in a single table, saving us the trouble of computing them ourselves. To install the gmodels package if you haven’t already done so using the instructions in the prior chapter, use the following command:
> install.packages("gmodels")
After the package installs, type library(gmodels) to load the package. Although you only need to install the package once, you will need to load the package with the library() command during each R session in which you plan to use the CrossTable() function.
Before proceeding with our analysis, let’s simplify our project by reducing the number of levels in the color variable. This variable has nine levels, but we don’t really need this much detail. What we are truly interested in is whether the car’s color is conservative. Toward this end, we’ll divide the nine colors into two groups—the first group will include the conservative colors black, gray, silver, and white; the second group will include blue, gold, green, red, and yellow. We’ll create a logical vector indicating whether the car’s color is conservative by our definition. The following returns TRUE if the car is one of the four conservative colors, and FALSE otherwise:
> usedcars$conservative <-
usedcars$color %in% c("Black", "Gray", "Silver", "White")
You may have noticed a new command here. The %in% operator returns TRUE or FALSE for each value in the vector on the left-hand side of the operator, indicating whether the value is found in the vector on the right-hand side. In simple terms, you can translate this line as “is the used car color in the set of black, gray, silver, and white?”
Examining the table() output for our newly created variable, we see that about two-thirds of the cars have conservative colors while one-third do not:
> table(usedcars$conservative)
FALSE TRUE
51 99
Now, let’s look at a cross-tabulation to see how the proportion of conservatively colored cars varies by model. Since we’re assuming that the model of car dictates the choice of color, we’ll treat the conservative color indicator as the dependent (y) variable. The CrossTable() command is therefore:
> CrossTable(x = usedcars$model, y = usedcars$conservative)
This results in the following table:
Cell Contents
|-------------------------|
| N |
| Chi-square-contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 150
| usedcars$conservative
usedcars$model | FALSE | TRUE | Row Total |
-----------------------|----------|-------------|-------------|
SE | 27 | 51 | 78 |
| 0.009 | 0.004 | |
| 0.346 | 0.654 | 0.520 |
| 0.529 | 0.515 | |
| 0.180 | 0.340 | |
-----------------------|----------|-------------|-------------|
SEL | 7 | 16 | 23 |
| 0.086 | 0.044 | |
| 0.304 | 0.696 | 0.153 |
| 0.137 | 0.612 | |
| 0.047 | 0.107 | |
-----------------------|----------|-------------|-------------|
SES | 17 | 32 | 49 |
| 0.007 | 0.004 | |
| 0.347 | 0.653 | 0.327 |
| 0.333 | 0.323 | |
| 0.113 | 0.213 | |
-----------------------|----------|-------------|-------------|
Column Total | 51 | 99 | 150 |
| 0.340 | 0.660 | |
-----------------------|----------|-------------|-------------|
The CrossTable() output is dense with numbers, but the legend at the top (labeled Cell Contents) indicates how to interpret each value. The table rows indicate the three models of used cars: SE, SEL, and SES (plus an additional row for the total across all models). The columns indicate whether the car’s color is conservative (plus a column totaling across both types of color).
The first value in each cell indicates the number of cars with that combination of model and color. The proportions indicate each cell’s contribution to the chi-square statistic, the row total, the column total, and the table’s overall total.
What we are most interested in is the proportion of conservative cars for each model. The row proportions tell us that 0.654 (65 percent) of SE cars are colored conservatively, in comparison to 0.696 (70 percent) of SEL cars, and 0.653 (65 percent) of SES. These differences are relatively small, which suggests that there are no substantial differences in the types of colors chosen for each model of car.
The chi-square values refer to the cell’s contribution in the Pearson’s chi-squared test for independence between two variables. Although a complete discussion of the statistics behind this test is highly technical, the test measures how likely it is that the difference in cell counts in the table is due to chance alone, which can help us confirm our hypothesis that the differences by group are not substantial. Beginning by adding the cell contributions for the six cells in the table, we find 0.009 + 0.004 + 0.086 + 0.044 + 0.007 + 0.004 = 0.154. This is the chi-squared test statistic.
To calculate the probability that this statistic is observed under the hypothesis that there is no association between the variables, we pass the test statistic to the pchisq() function as follows:
> pchisq(0.154, df = 2, lower.tail = FALSE)
[1] 0.9258899
The df parameter refers to the degrees of freedom, which is a component of the statistical test related to the number of rows and columns in the table; again, ignoring what it means, it can be computed as (rows - 1) * (columns - 1), or 1 for a 2x2 table and 2 for the 3x2 table used here. Setting lower.tail = FALSE requests the right-tailed probability of about 0.926, which can be understood intuitively as the probability of obtaining a test statistic of at least 0.154 or greater due to chance alone.
If the probability of the chi-squared test is very low—perhaps below ten, five, or even one percent—it provides strong evidence that the two variables are associated, because the observed association in the table is unlikely to have happened by chance. In our case, the probability is much closer to 100 percent than to 10 percent, so it is unlikely we are observing an association between model and color for cars in this dataset.
Rather than computing this by hand, you can also obtain the chi-squared test results by adding an additional parameter specifying chisq = TRUE when calling the CrossTable() function. For example:
> CrossTable(x = usedcars$model, y = usedcars$conservative,
chisq = TRUE)
Pearson's Chi-squared test
------------------------------------------------------------
Chi^2 = 0.1539564 d.f. = 2 p = 0.92591
Note that, aside from slight differences due to rounding, this produces the same chi-squared test statistic and probability as was computed by hand.
The chi-squared test performed here is one of many types of formal hypothesis testing that can be performed using traditional statistics. If you’ve ever heard the phrase “statistically significant,” it means a statistical test like chi-squared (or one of many others) was performed, and it reached a “significant” level—typically, a probability less than five percent. Although hypothesis testing is somewhat beyond the scope of this book, it will be encountered again briefly in Chapter 6, Forecasting Numeric Data – Regression Methods.
Summary
In this chapter, we learned about the basics of managing data in R. We started by taking an in-depth look at the structures used for storing various types of data. The foundational R data structure is the vector, which is extended and combined into more complex data types, such as lists and data frames. The data frame is an R data structure that corresponds to the notion of a dataset having both features and examples. R provides functions for reading and writing data frames to spreadsheet-like tabular data files.
We then explored a real-world dataset containing the prices of used cars. We examined numeric variables using common summary statistics of center and spread, and visualized relationships between prices and odometer readings with a scatterplot. Next, we examined nominal variables using tables. In examining the used car data, we followed an exploratory process that can be used to understand any dataset. These skills will be required for the other projects throughout this book.
Now that we have spent some time understanding the basics of data management with R, you are ready to begin using machine learning to solve real-world problems. In the next chapter, we will tackle our first classification task using nearest neighbor methods. You may be surprised to discover that with just a few lines of R code, a machine can achieve human-like performance on a challenging medical diagnosis task.
Join our book’s Discord space
Join our Discord community to meet like-minded people and learn alongside more than 4000 people at:






















 Download code from GitHub
Download code from GitHub
