Introduction - Machine Learning and Statistical Science
Machine learning has definitely been one of the most talked about fields in recent years, and for good reason. Every day new applications and models are discovered, and researchers around the world announce impressive advances in the quality of results on a daily basis.
Each day, many new practitioners decide to take courses and search for introductory materials so they can employ these newly available techniques that will improve their applications. But in many cases, the whole corpus of machine learning, as normally explained in the literature, requires a good understanding of mathematical concepts as a prerequisite, thus imposing a high bar for programmers who typically have good algorithmic skills but are less familiar with higher mathematical concepts.
This first chapter will be a general introduction to the field, covering the main study areas of machine learning, and will offer an overview of the basic statistics, probability, and calculus, accompanied by source code examples in a way that allows you to experiment with the provided formulas and parameters.
In this first chapter, you will learn the following topics:
- What is machine learning?
- Machine learning areas
- Elements of statistics and probability
- Elements of calculus
The world around us provides huge amounts of data. At a basic level, we are continually acquiring and learning from text, image, sound, and other types of information surrounding us. The availability of data, then, is the first step in the process of acquiring the skills to perform a task.
A myriad of computing devices around the world collect and store an overwhelming amount of information that is image-, video-, and text-based. So, the raw material for learning is clearly abundant, and it's available in a format that a computer can deal with.
That's the starting point for the rise of the discipline discussed in this book: the study of techniques and methods allowing computers to learn from data without being explicitly programmed.
A more formal definition of machine learning, from Tom Mitchell, is as follows:
This definition is complete, and reinstates the elements that play a role in every machine learning project: the task to perform, the successive experiments, and a clear and appropriate performance measure. In simpler words, we have a program that improves how it performs a task based on experience and guided by a certain criterion.
Machine learning in the bigger picture
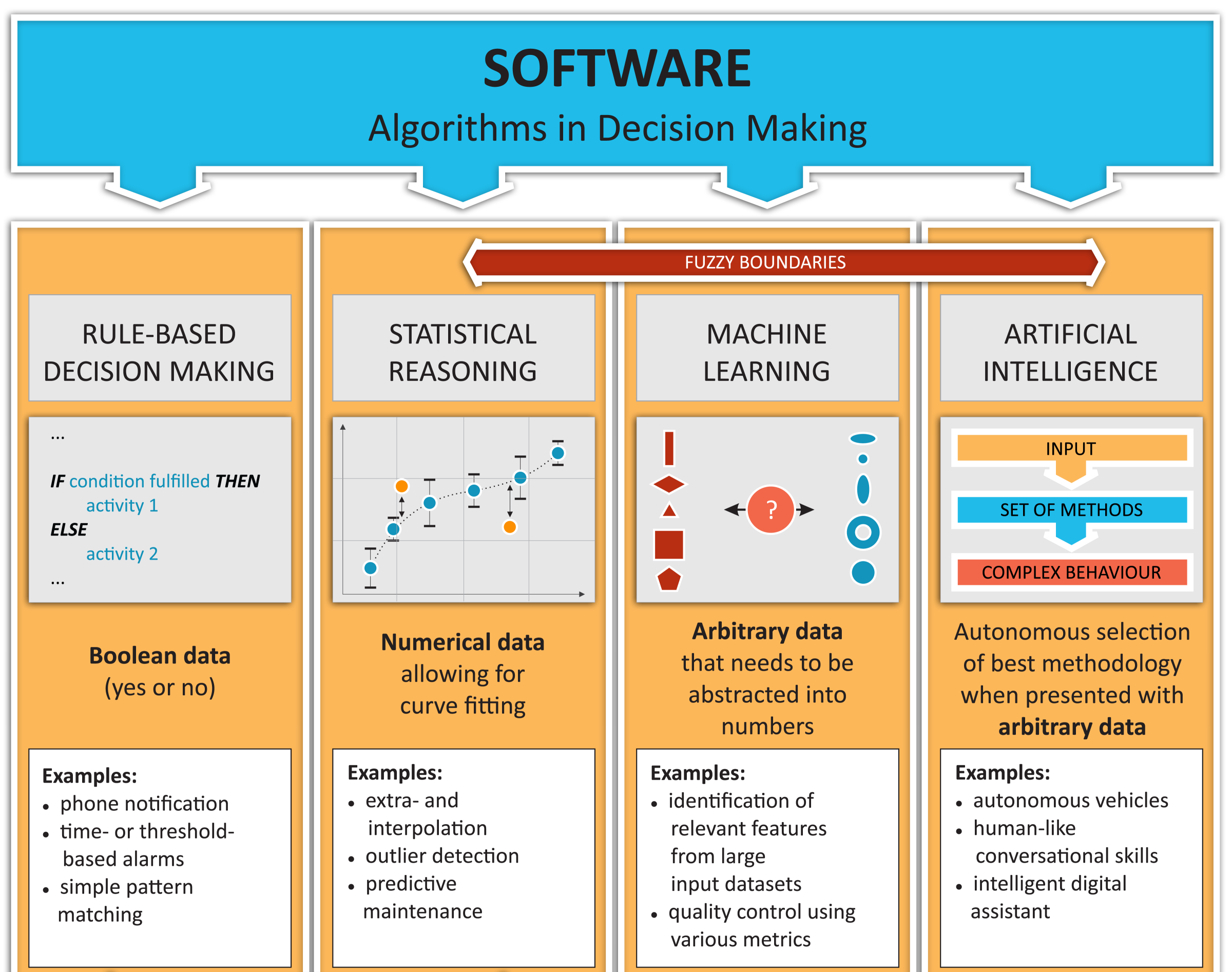
Machine learning as a discipline is not an isolated field—it is framed inside a wider domain, Artificial Intelligence (AI). But as you can guess, machine learning didn't appear from the void. As a discipline it has its predecessors, and it has been evolving in stages of increasing complexity in the following four clearly differentiated steps:
- The first model of machine learning involved rule-based decisions and a simple level of data-based algorithms that includes in itself, and as a prerequisite, all the possible ramifications and decision rules, implying that all the possible options will be hardcoded into the model beforehand by an expert in the field. This structure was implemented in the majority of applications developed since the first programming languages appeared in 1950. The main data type and function being handled by this kind of algorithm is the Boolean, as it exclusively dealt with yes or no decisions.
- During the second developmental stage of statistical reasoning, we started to let the probabilistic characteristics of the data have a say, in addition to the previous choices set up in advance. This better reflects the fuzzy nature of real-world problems, where outliers are common and where it is more important to take into account the nondeterministic tendencies of the data than the rigid approach of fixed questions. This discipline adds to the mix of mathematical tools elements of Bayesian probability theory. Methods pertaining to this category include curve fitting (usually of linear or polynomial), which has the common property of working with numerical data.
- The machine learning stage is the realm in which we are going to be working throughout this book, and it involves more complex tasks than the simplest Bayesian elements of the previous stage.
The most outstanding feature of machine learning algorithms is that they can generalize models from data but the models are capable of generating their own feature selectors, which aren't limited by a rigid target function, as they are generated and defined as the training process evolves. Another differentiator of this kind of model is that they can take a large variety of data types as input, such as speech, images, video, text, and other data susceptible to being represented as vectors. - AI is the last step in the scale of abstraction capabilities that, in a way, include all previous algorithm types, but with one key difference: AI algorithms are able to apply the learned knowledge to solve tasks that had never been considered during training. The types of data with which this algorithm works are even more generic than the types of data supported by machine learning, and they should be able, by definition, to transfer problem-solving capabilities from one data type to another, without a complete retraining of the model. In this way, we could develop an algorithm for object detection in black and white images and the model could abstract the knowledge to apply the model to color images.
In the following diagram, we represent these four stages of development towards real AI applications:
Types of machine learning
Let's try to dissect the different types of machine learning project, starting from the grade of previous knowledge from the point of view of the implementer. The project can be of the following types:
- Supervised learning: In this type of learning, we are given a sample set of real data, accompanied by the result the model should give us after applying it. In statistical terms, we have the outcome of all the training set experiments.
- Unsupervised learning: This type of learning provides only the sample data from the problem domain, but the task of grouping similar data and applying a category has no previous information from which it can be inferred.
- Reinforcement learning: This type of learning doesn't have a labeled sample set and has a different number of participating elements, which include an agent, an environment, and learning an optimum policy or set of steps, maximizing a goal-oriented approach by using rewards or penalties (the result of each attempt).
Take a look at the following diagram:

Grades of supervision
The learning process supports gradual steps in the realm of supervision:
- Unsupervised Learning doesn't have previous knowledge of the class or value of any sample, it should infer it automatically.
- Semi-Supervised Learning, needs a seed of known samples, and the model infers the remaining samples class or value from that seed.
- Supervised Learning: This approach normally includes a set of known samples, called training set, another set used to validate the model's generalization, and a third one, called test set, which is used after the training process to have an independent number of samples outside of the training set, and warranty independence of testing.
In the following diagram, depicts the mentioned approaches:

Supervised learning strategies - regression versus classification
This type of learning has the following two main types of problem to solve:
- Regression problem: This type of problem accepts samples from the problem domain and, after training the model, minimizes the error by comparing the output with the real answers, which allows the prediction of the right answer when given a new unknown sample
- Classification problem: This type of problem uses samples from the domain to assign a label or group to new unknown samples
Unsupervised problem solving–clustering
The vast majority of unsupervised problem solving consist of grouping items by looking at similarities or the value of shared features of the observed items, because there is no certain information about the a priori classes. This type of technique is called clustering.
Outside of these main problem types, there is a mix of both, which is called semi-supervised problem solving, in which we can train a labeled set of elements and also use inference to assign information to unlabeled data during training time. To assign data to unknown entities, three main criteria are used—smoothness (points close to each other are of the same class), cluster (data tends to form clusters, a special case of smoothness), and manifold (data pertains to a manifold of much lower dimensionality than the original domain).
Tools of the trade–programming language and libraries
As this book is aimed at developers, we think that the approach of explaining the mathematical concepts using real code comes naturally.
When choosing the programming language for the code examples, the first approach was to use multiple technologies, including some cutting-edge libraries. After consulting the community, it was clear that a simple language would be preferable when explaining the concepts.
Among the options, the ideal candidate would be a language that is simple to understand, with real-world machine learning adoption, and that is also relevant.
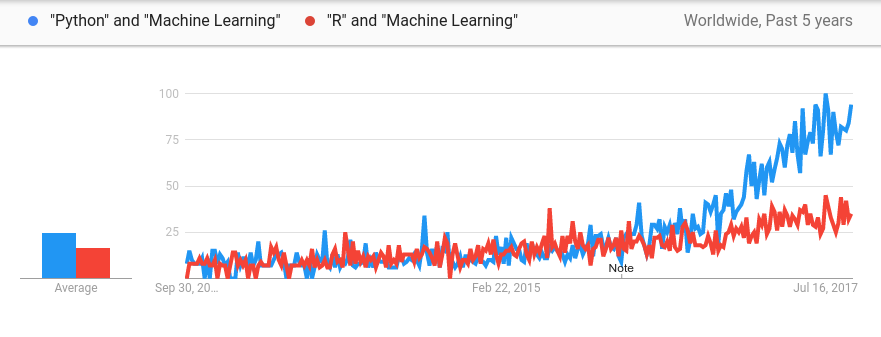
The clearest candidate for this task was Python, which fulfils all these conditions, and especially in the last few years has become the go-to language for machine learning, both for newcomers and professional practitioners.
In the following graph, we compare the previous star in the machine learning programming language field, R, and we can clearly conclude the huge, favorable tendency towards using Python. This means that the skills you acquire in this book will be relevant now and in the foreseeable future:
In addition to Python code, we will have the help of a number of the most well-known numerical, statistical, and graphical libraries in the Python ecosystem, namely pandas, NumPy, and matplotlib. For the deep neural network examples, we will use the Keras library, with TensorFlow as the backend.
The Python language
Python is a general-purpose scripting language, created by the Dutch programmer Guido Van Rossum in 1989. It possesses a very simple syntax with great extensibility, thanks to its numerous extension libraries, making it a very suitable language for prototyping and general coding. Because of its native C bindings, it can also be a candidate for production deployment.
The language is actually used in a variety of areas, ranging from web development to scientific computing, in addition to its use as a general scripting tool.
The NumPy library
If we had to choose a definitive must-use library for use in this book, and a non-trivial mathematical application written in Python, it would have to be NumPy. This library will help us implement applications using statistics and linear algebra routines with the following components:
- A versatile and performant N-dimensional array object
- Many mathematical functions that can be applied to these arrays in a seamless manner
- Linear algebra primitives
- Random number distributions and a powerful statistics package
- Compatibility with all the major machine learning packages
The matplotlib library
Data plotting is an integral part of data science and is normally the first step an analyst performs to get a sense of what's going on in the provided set of data.
For this reason, we need a very powerful library to be able to graph the input data, and also to represent the resulting output. In this book, we will use Python's matplotlib library to describe concepts and the results from our models.
What's matplotlib?
Matplotlib is an extensively used plotting library, especially designed for 2D graphs. From this library, we will focus on using the pyplot module, which is a part of the API of matplotlib and has MATLAB-like methods, with direct NumPy support. For those of you not familiar with MATLAB, it has been the default mathematical notebook environment for the scientific and engineering fields for decades.
The method described will be used to illustrate a large proportion of the concepts involved, and in fact, the reader will be able to generate many of the examples in this book with just these two libraries, and using the provided code.
Pandas
Pandas complements the previously mentioned libraries with a special structure, called DataFrame, and also adds many statistical and data mangling methods, such as I/O, for many different formats, such as slicing, subsetting, handling missing data, merging, and reshaping, among others.
The DataFrame object is one of the most useful features of the whole library, providing a special 2D data structure with columns that can be of different data types. Its structure is very similar to a database table, but immersed in a flexible programming runtime and ecosystem, such as SciPy. These data structures are also compatible with NumPy matrices, so we can also apply high-performance operations to the data with minimal effort.
SciPy
SciPy is a stack of very useful scientific Python libraries, including NumPy, pandas, matplotlib, and others, but it also the core library of the ecosystem, with which we can also perform many additional fundamental mathematical operations, such as integration, optimization, interpolation, signal processing, linear algebra, statistics, and file I/O.
Jupyter notebook
Jupyter is a clear example of a successful Python-based project, and it's also one of the most powerful devices we will employ to explore and understand data through code.
Jupyter notebooks are documents consisting of intertwined cells of code, graphics, or formatted text, resulting in a very versatile and powerful research environment. All these elements are wrapped in a convenient web interface that interacts with the IPython interactive interpreter.
Once a Jupyter notebook is loaded, the whole environment and all the variables are in memory and can be changed and redefined, allowing research and experimentation, as shown in the following screenshot:

This tool will be an important part of this book's teaching process, because most of the Python examples will be provided in this format. In the last chapter of the book, you will find the full installation instructions.
Basic mathematical concepts
As we saw in the previous sections, this main target audience of the book is developers who want to understand machine learning algorithms. But in order to really grasp the motivations and reason behind them, it's necessary to review and build all the fundamental reasoning, which includes statistics, probability, and calculus.
We will first start with some of the fundamentals of statistics.
Statistics - the basic pillar of modeling uncertainty
Statistics can be defined as a discipline that uses data samples to extract and support conclusions about larger samples of data. Given that machine learning comprises a big part of the study of the properties of data and the assignment of values to data, we will use many statistical concepts to define and justify the different methods.
Descriptive statistics - main operations
In the following sections, we will start defining the fundamental operations and measures of the discipline of statistics in order to be able to advance from the fundamental concepts.
Mean
This is one of the most intuitive and most frequently used concepts in statistics. Given a set of numbers, the mean of that set is the sum of all the elements divided by the number of elements in the set.
The formula that represents the mean is as follows:

Although this is a very simple concept, we will write a Python code sample in which we will create a sample set, represent it as a line plot, and mark the mean of the whole set as a line, which should be at the weighted center of the samples. It will serve as an introduction to Python syntax, and also as a way of experimenting with Jupyter notebooks:
import matplotlib.pyplot as plt #Import the plot library
def mean(sampleset): #Definition header for the mean function
total=0
for element in sampleset:
total=total+element
return total/len(sampleset)
myset=[2.,10.,3.,6.,4.,6.,10.] #We create the data set
mymean=mean(myset) #Call the mean funcion
plt.plot(myset) #Plot the dataset
plt.plot([mymean] * 7) #Plot a line of 7 points located on the mean
This program will output a time series of the dataset elements, and will then draw a line at the mean height.
As the following graph shows, the mean is a succinct (one value) way of describing the tendency of a sample set:

In this first example, we worked with a very homogeneous sample set, so the mean is very informative regarding its values. But let's try the same sample with a very dispersed sample set (you are encouraged to play with the values too):

Variance
As we saw in the first example, the mean isn't sufficient to describe non-homogeneous or very dispersed samples.
In order to add a unique value describing how dispersed the sample set's values are, we need to look at the concept of variance, which needs the mean of the sample set as a starting point, and then averages the distances of the samples from the provided mean. The greater the variance, the more scattered the sample set.
The canonical definition of variance is as follows:

Let's write the following sample code snippet to illustrate this concept, adopting the previously used libraries. For the sake of clarity, we are repeating the declaration of the mean function:
import math #This library is needed for the power operation
def mean(sampleset): #Definition header for the mean function
total=0
for element in sampleset:
total=total+element
return total/len(sampleset)
def variance(sampleset): #Definition header for the mean function
total=0
setmean=mean(sampleset)
for element in sampleset:
total=total+(math.pow(element-setmean,2))
return total/len(sampleset)
myset1=[2.,10.,3.,6.,4.,6.,10.] #We create the data set
myset2=[1.,-100.,15.,-100.,21.]
print "Variance of first set:" + str(variance(myset1))
print "Variance of second set:" + str(variance(myset2))
The preceding code will generate the following output:
Variance of first set:8.69387755102
Variance of second set:3070.64
As you can see, the variance of the second set was much higher, given the really dispersed values. The fact that we are computing the mean of the squared distance helps to really outline the differences, as it is a quadratic operation.
Standard deviation
Standard deviation is simply a means of regularizing the square nature of the mean square used in the variance, effectively linearizing this term. This measure can be useful for other, more complex operations.
Here is the official form of standard deviation:

Probability and random variables
We are now about to study the single most important discipline required for understanding all the concepts of this book.
Probability is a mathematical discipline, and its main occupation is the study of random events. In a more practical definition, probability normally tries to quantify the level of certainty (or conversely, uncertainty) associated with an event, from a universe of possible occurrences.
Events
In order to understand probabilities, we first need to define events. An event is, given an experiment in which we perform a determined action with different possible results, a subset of all the possible outcomes for that experiment.
Examples of events are a particular dice number appearing, and a product defect of particular type appearing on an assembly line.
Probability
Following the previous definitions, probability is the likelihood of the occurrence of an event. Probability is quantified as a real number between 0 and 1, and the assigned probability P increases towards 1 when the likelihood of the event occurring increases.
The mathematical expression for the probability of the occurrence of an event is P(E).
Random variables and distributions
When assigning event probabilities, we could also try to cover the entire sample and assign one probability value to each of the possible outcomes for the sample domain.
This process does indeed have all the characteristics of a function, and thus we will have a random variable that will have a value for each one of the possible event outcomes. We will call this function a random function.
These variables can be of the following two types:
- Discrete: If the number of outcomes is finite, or countably infinite
- Continuous: If the outcome set belongs to a continuous interval
This probability function is also called probability distribution.
Useful probability distributions
Between the multiple possible probability distributions, there are a number of functions that have been studied and analyzed for their special properties, or the popular problems they represent.
We will describe the most common ones that have a special effect on the development of machine learning.
Bernoulli distributions
Let's begin with a simple distribution: one that has a binary outcome, and is very much like tossing a (fair) coin.
This distribution represents a single event that takes the value 1 (let's call this heads) with a probability of p, and 0 (lets call this tails), with probability 1-p.
In order to visualize this, let's generate a large number of events of a Bernoulli distribution using np and graph the tendency of this distribution, with the following only two possible outcomes:
plt.figure()
distro = np.random.binomial(1, .6, 10000)/0.5
plt.hist(distro, 2 , normed=1)
The following graph shows the binomial distribution, through an histogram, showing the complementary nature of the outcomes' probabilities:

So, here we see the very clear tendency of the complementing probabilities of the possible outcomes. Now let's complement the model with a larger number of possible outcomes. When their number is greater than 2, we are talking about a multinomial distribution:
plt.figure()
distro = np.random.binomial(100, .6, 10000)/0.01
plt.hist(distro, 100 , normed=1)
plt.show()
Take a look at the following graph:

Uniform distribution
This very common distribution is the first continuous distribution that we will see. As the name implies, it has a constant probability value for any interval of the domain.
In order to integrate to 1, a and b being the extreme of the function, this probability has the value of 1/(b-a).
Let's generate a plot with a sample uniform distribution using a very regular histogram, as generated by the following code:
plt.figure()
uniform_low=0.25
uniform_high=0.8
plt.hist(uniform, 50, normed=1)
plt.show()
Take look at the following graph:

Normal distribution
This very common continuous random function, also called a Gaussian function, can be defined with the simple metrics of the mean and the variance, although in a somewhat complex form.
This is the canonical form of the function:

Take a look at the following code snippet:
import matplotlib.pyplot as plt #Import the plot library
import numpy as np
mu=0.
sigma=2.
distro = np.random.normal(mu, sigma, 10000)
plt.hist(distro, 100, normed=True)
plt.show()
The following graph shows the generated distribution's histogram:

Logistic distribution
This distribution is similar to the normal distribution, but with the morphological difference of having a more elongated tail. The main importance of this distribution lies in its cumulative distribution function (CDF), which we will be using in the following chapters, and will certainly look familiar.
Let's first represent the base distribution by using the following code snippet:
import matplotlib.pyplot as plt #Import the plot library
import numpy as np
mu=0.5
sigma=0.5
distro2 = np.random.logistic(mu, sigma, 10000)
plt.hist(distro2, 50, normed=True)
distro = np.random.normal(mu, sigma, 10000)
plt.hist(distro, 50, normed=True)
plt.show()
Take a look at the following graph:

Then, as mentioned before, let's compute the CDF of the logistic distribution so that you will see a very familiar figure, the sigmoid curve, which we will see again when we review neural network activation functions:
plt.figure()
logistic_cumulative = np.random.logistic(mu, sigma, 10000)/0.02
plt.hist(logistic_cumulative, 50, normed=1, cumulative=True)
plt.show()
Take a look at the following graph:

Statistical measures for probability functions
In this section, we will see the most common statistical measures that can be applied to probabilities. The first measures are the mean and variance, which do not differ from the definitions we saw in the introduction to statistics.
Skewness
This measure represents the lateral deviation, or in general terms, the deviation from the center, or the symmetry (or lack thereof) of a probability distribution. In general, if skewness is negative, it implies a deviation to the right, and if it is positive, it implies a deviation to the left:

Take a look at the following diagram, which depicts the skewness statistical distribution:

Kurtosis
Kurtosis gives us an idea of the central concentration of a distribution, defining how acute the central area is, or the reverse—how distributed the function's tail is.
The formula for kurtosis is as follows:

In the following diagram, we can clearly see how the new metrics that we are learning can be intuitively understood:

Differential calculus elements
To cover the minimum basic knowledge of machine learning, especially the learning algorithms such as gradient descent, we will introduce you to the concepts involved in differential calculus.
Preliminary knowledge
Covering the calculus terminology necessary to get to gradient descent theory would take many chapters, so we will assume you have an understanding of the concepts of the properties of the most well-known continuous functions, such as linear, quadratic, logarithmic, and exponential, and the concept of limit.
For the sake of clarity, we will develop the concept of the functions of one variable, and then expand briefly to cover multivariate functions.
In search of changes–derivatives
We established the concept of functions in the previous section. With the exception of constant functions defined in the entire domain, all functions have some sort of value dynamics. That means that f(x1) is different than f(x2) for some determined values of x.
The purpose of differential calculus is to measure change. For this specific task, many mathematicians of the 17th century (Leibniz and Newton were the most prominent exponents) worked hard to find a simple model to measure and predict how a symbolically defined function changed over time.
This research guided the field to one wonderful concept—a symbolic result that, under certain conditions, tells you how much and in which direction a function changes at a certain point. This is the concept of a derivative.
Sliding on the slope
If we want to measure how a function changes over time, the first intuitive step would be to take the value of a function and then measure it at the subsequent point. Subtracting the second value from the first would give us an idea of how much the function changes over time:
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
def quadratic(var):
return 2* pow(var,2)
x=np.arange(0,.5,.1)
plt.plot(x,quadratic(x))
plt.plot([1,4], [quadratic(1), quadratic(4)], linewidth=2.0)
plt.plot([1,4], [quadratic(1), quadratic(1)], linewidth=3.0,
label="Change in x")
plt.plot([4,4], [quadratic(1), quadratic(4)], linewidth=3.0,
label="Change in y")
plt.legend()
plt.plot (x, 10*x -8 )
plt.plot()
In the preceding code example, we first defined a sample quadratic equation (2*x2) and then defined the part of the domain in which we will work with the arange function (from 0 to 0.5, in 0.1 steps).
Then, we define an interval for which we measure the change of y over x, and draw lines indicating this measurement, as shown in the following graph:

In this case, we measure the function at x=1 and x=4, and define the rate of change for this interval as follows:

Applying the formula, the result for the sample is (36-0)/3= 12.
This initial approach can serve as a way of approximately measuring this dynamic, but it's too dependent on the points at which we take the measurement, and it has to be taken at every interval we need.
To have a better idea of the dynamics of a function, we need to be able to define and measure the instantaneous change rate at every point in the function's domain.
This idea of instantaneous change brings to us the need to reduce the distance between the domain's x values, taken at a point where there are very short distances between them. We will formulate this approach with an initial value x, and the subsequent value, x + Δx:

In the following code, we approximate the difference, reducing Δx progressively:
initial_delta = .1
x1 = 1
for power in range (1,6):
delta = pow (initial_delta, power)
derivative_aprox= (quadratic(x1+delta) - quadratic (x1) )/
((x1+delta) - x1 )
print "del ta: " + str(delta) + ", estimated derivative: " +
str(derivative_aprox)
In the preceding code, we first defined an initial delta, which brought an initial approximation. Then, we apply the difference function, with diminishing values of delta, thanks us to powering 0.1 with incremental powers. The results we get are as follows:
delta: 0.1, estimated derivative: 4.2
delta: 0.01, estimated derivative: 4.02
delta: 0.001, estimated derivative: 4.002
delta: 0.0001, estimated derivative: 4.0002
delta: 1e-05, estimated derivative: 4.00002
As the separation diminishes, it becomes clear that the change rate will hover around 4. But when does this process stop? In fact, we could say that this process can be followed ad infinitum, at least in a numeric sense.
This is when the concept of limit intuitively appears. We will then define this process, of making Δ indefinitely smaller, and will call it the derivative of f(x) or f'(x):

This is the formal definition of the derivative.
But mathematicians didn't stop with these tedious calculations, making a large number of numerical operations (which were mostly done manually of the 17th century), and wanted to further simplify these operations.
What if we perform another step that can symbolically define the derivative of a function?
That would require building a function that gives us the derivative of the corresponding function, just by replacing the x variable value. That huge step was also reached in the 17th century, for different function families, starting with the parabolas (y=x2+b), and following with more complex functions:

Chain rule
One very important result of the symbolic determination of a function's derivative is the chain rule. This formula, first mentioned in a paper by Leibniz in 1676, made it possible to solve the derivatives of composite functions in a very simple and elegant manner, simplifying the solution for very complex functions.
In order to define the chain rule, if we suppose a function f, which is defined as a function of another function g, f(g(x)) of F, the derivative can be defined as follows:

The formula of the chain rule allows us to differentiate formulas whose input values depend on another function. This is the same as searching the rate of change of a function that is linked to a previous one. The chain rule is one of the main theoretical concepts employed in the training phase of neural networks, because in those layered structures, the output of the first neuron layers will be the inputs of the following, giving, as a result, a composite function that, most of the time, is of more than one nesting level.
Partial derivatives
Until now we've been working with univariate functions, but the type of function we will mostly work with from now on will be multivariate, as the dataset will contain much more than one column and each one of them will represent a different variable.
In many cases, we will need to know how the function changes in a relationship with only one dimension, which will involve looking at how one column of the dataset contributes to the total number of function changes.
The calculation of partial derivatives consists of applying the already known derivation rules to the multivariate function, considering the variables are not being derived as constant.
Take a look at the following power rule:
f(x,y) = 2x3y
When differentiating this function with respect to x, considering y a constant, we can rewrite it as 3 . 2 y x2, and applying the derivative to the variable x allows us to obtain the following derivative:
d/dx (f(x,y)) = 6y*x2
Using these techniques, we can proceed with the more complex multivariate functions, which will be part of our feature set, normally consisting of much more than two variables.
Summary
In this chapter, we worked through many different conceptual elements, including an overview of some basic mathematical concepts, which serve as a base for the machine learning concepts.
These concepts will be useful when we formally explain the mechanisms of the different modeling methods, and we encourage you to improve your understanding of them as much as possible, before and while reading the chapters, to better grasp how the algorithm works.
In the next chapter, we will have a quick overview of the the the complete workflow of a machine learning project, which will help us to understand the various elements involved, from data gathering to result evaluation.




















 Download code from GitHub
Download code from GitHub

