Mathematics is the language of physics and the foundation of computer science. Since quantum computing evolved from these two disciplines, it is essential to understand the mathematics behind it. The math you need is linear in nature, and that is where we will start. By the time we are done, you will have the mathematical foundation to fundamentally understand quantum computing. Let's get started!

In this chapter, we are going to cover the following main topics:

• Vectors
• Linear combinations
• Superposition

A long time ago in a country far, far away, there lived an ancient Greek mathematician named Euclid. He wrote a book that defined space using only three dimensions. We will use his vector space to define superposition in quantum computing. Don't be fooled—vector spaces have evolved tremendously since Euclid's days, and our definition of them will evolve too as the book progresses. But for now, we will stick to real numbers, and we'll actually only need two out of the three dimensions Euclid proposed.

To start, we will define a Euclidean vector as being a line segment with a length or magnitude and pointing in a certain direction, as shown in the following screenshot:

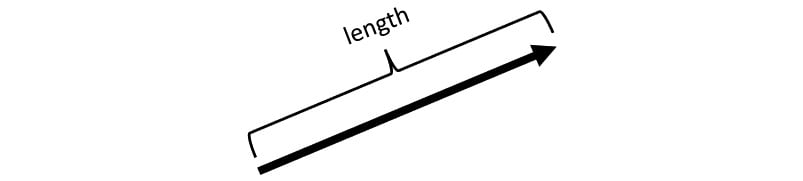
Figure 1.1 – Euclidean vector

Two vectors are equal if they have the same length and direction, so the following vectors are all equal:

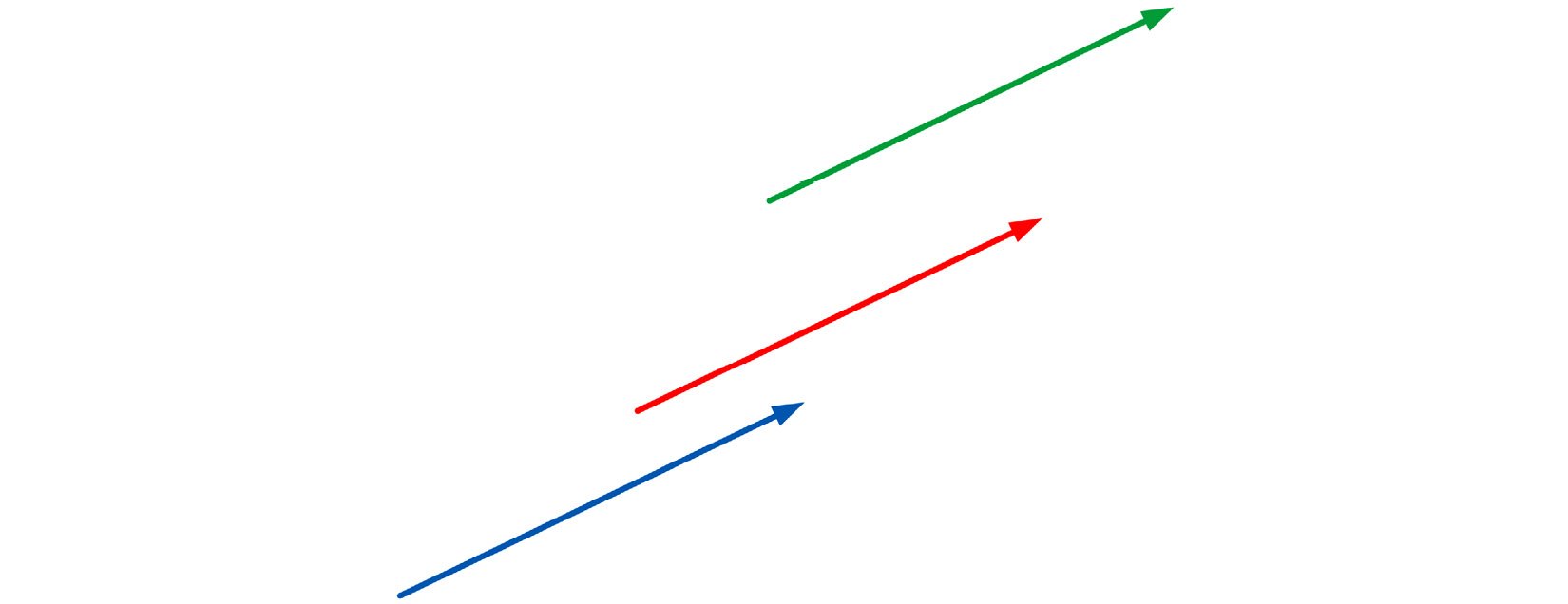
Figure 1.2 – Equal vectors

Vectors can be represented algebraically by their components. The simplest way to do this is to have them start at the origin (the point (0,0)) and use their x and y coordinates, as shown in the following screenshot:

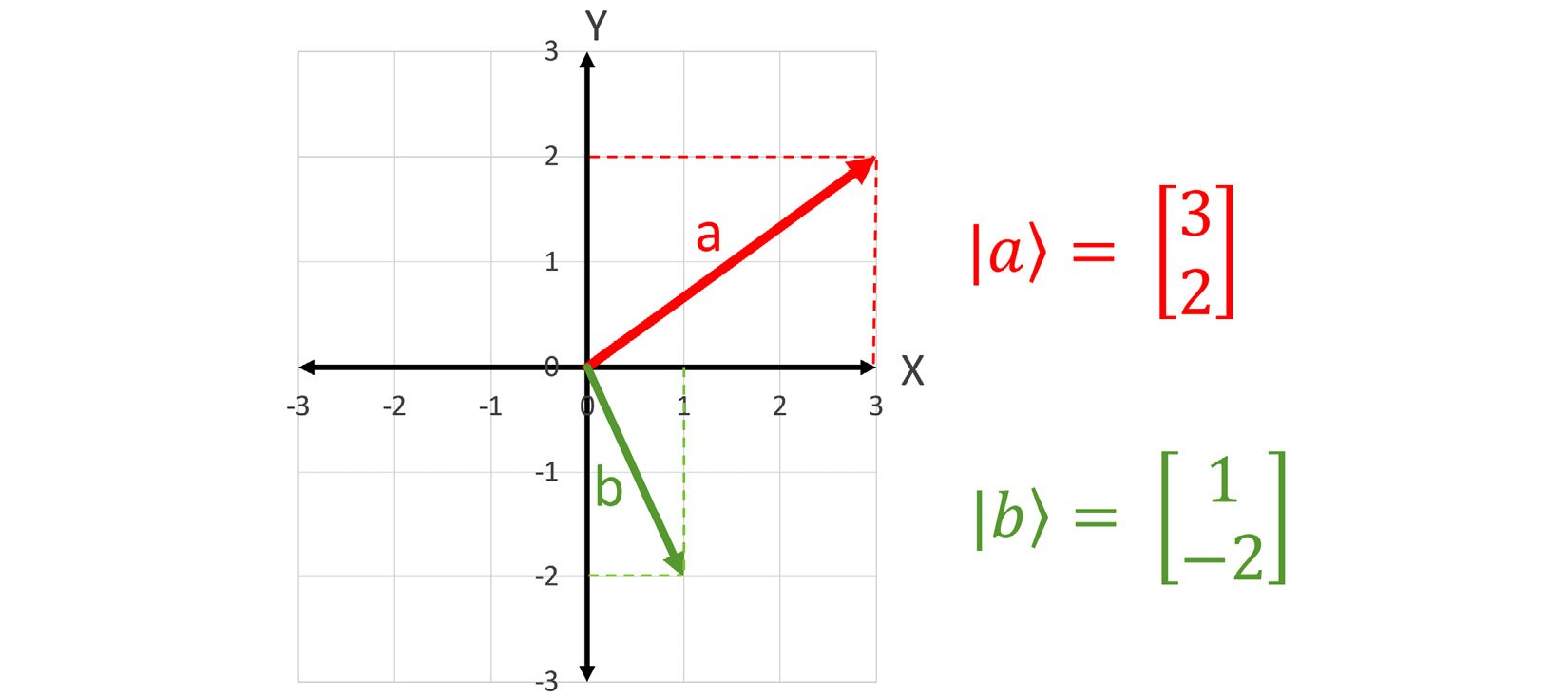
Figure 1.3 – Vectors represented geometrically and algebraically

You should note that I am using a special notation to label the vectors. It is called bra-ket notation. The appendix has more information on this notation, but for now, we will use a vertical bar or pipe, |, followed by the variable name for the vector and then an angle bracket, ⟩, to denote a vector (for example, |a⟩). The coordinates of our vectors will be enclosed in brackets [ ]. The x coordinate will be on top and the y coordinate on the bottom. Vectors are also called "kets" in this notation—for example, ket a, but for now, we will stick with the name vector.

Vector addition

So, it ends up that we can add vectors together both geometrically and algebraically, as shown in the following screenshot:

Figure 1.4 – Vector addition

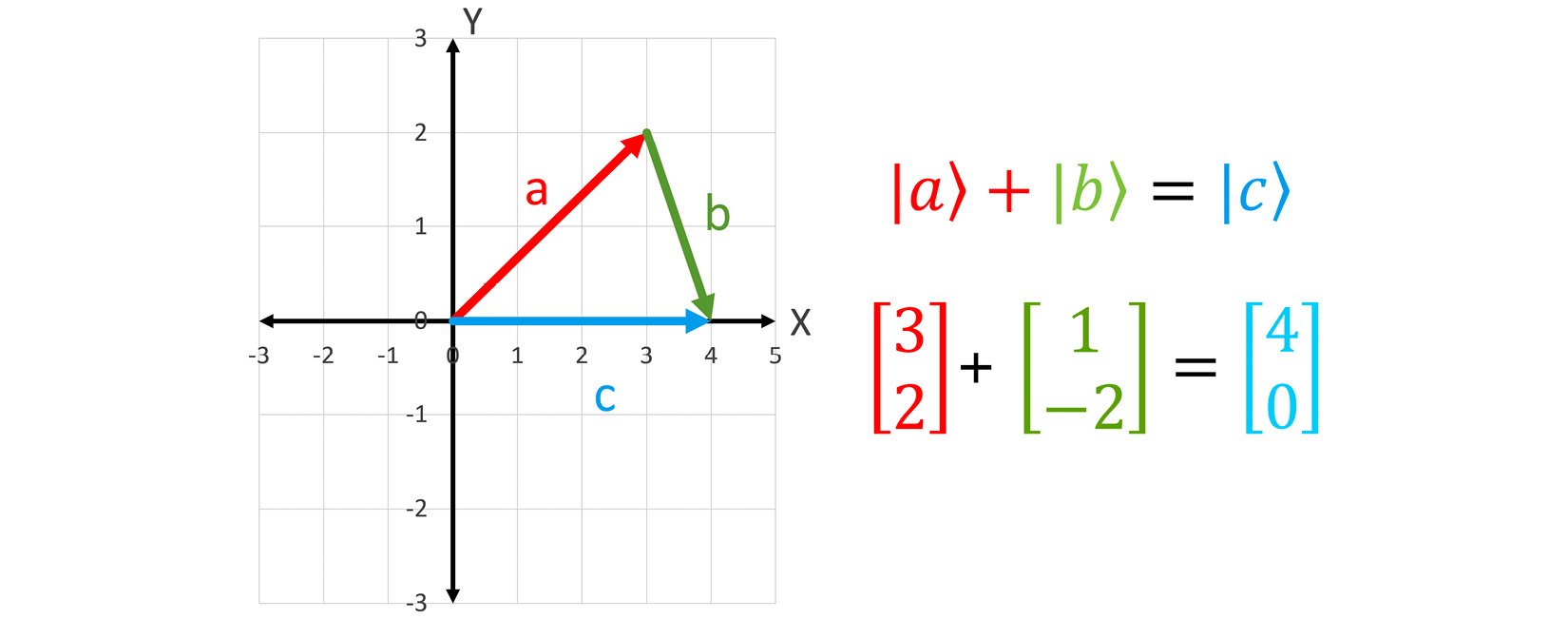
As you can see, we can take vectors and move them in the XY-plane as long as we preserve their length and direction. We have taken the vector |b⟩ from our first graph and moved its start position to the end of vector |a⟩. Once we do that, we can draw a third vector |c⟩ that connects the start of |a⟩ and the end of |b⟩ to form their sum. If we look at the coordinates of |c⟩, it is four units in the x direction and zero units in the y direction. This corresponds to the answer we see on the right of Figure 1.4.

We can also do this addition without the help of a graph, as shown on the right of Figure 1.4. Just adding the first components (3 and 1) gives 4, and adding the second components of the vectors (2 and -2) gives 0. Thus, vector addition works both geometrically and algebraically in two dimensions. So, let's look at an example.

Example

What is the sum of |m⟩ and |n⟩ here?

The solution is:

Exercise 1

Now, you try. The answers are at the end of this chapter:

• What is |m⟩ - |n⟩?
• What is |n⟩ - |m⟩?
• Solve the following expression (notice we use three-dimensional (3D) vectors, but everything works the same):

Scalar multiplication

We can also multiply our vectors by numbers or scalars. They are called scalars because they "scale" a vector, as we will see. The following screenshot shows a vector that is multiplied by a number on the left and the same thing algebraically on the right:

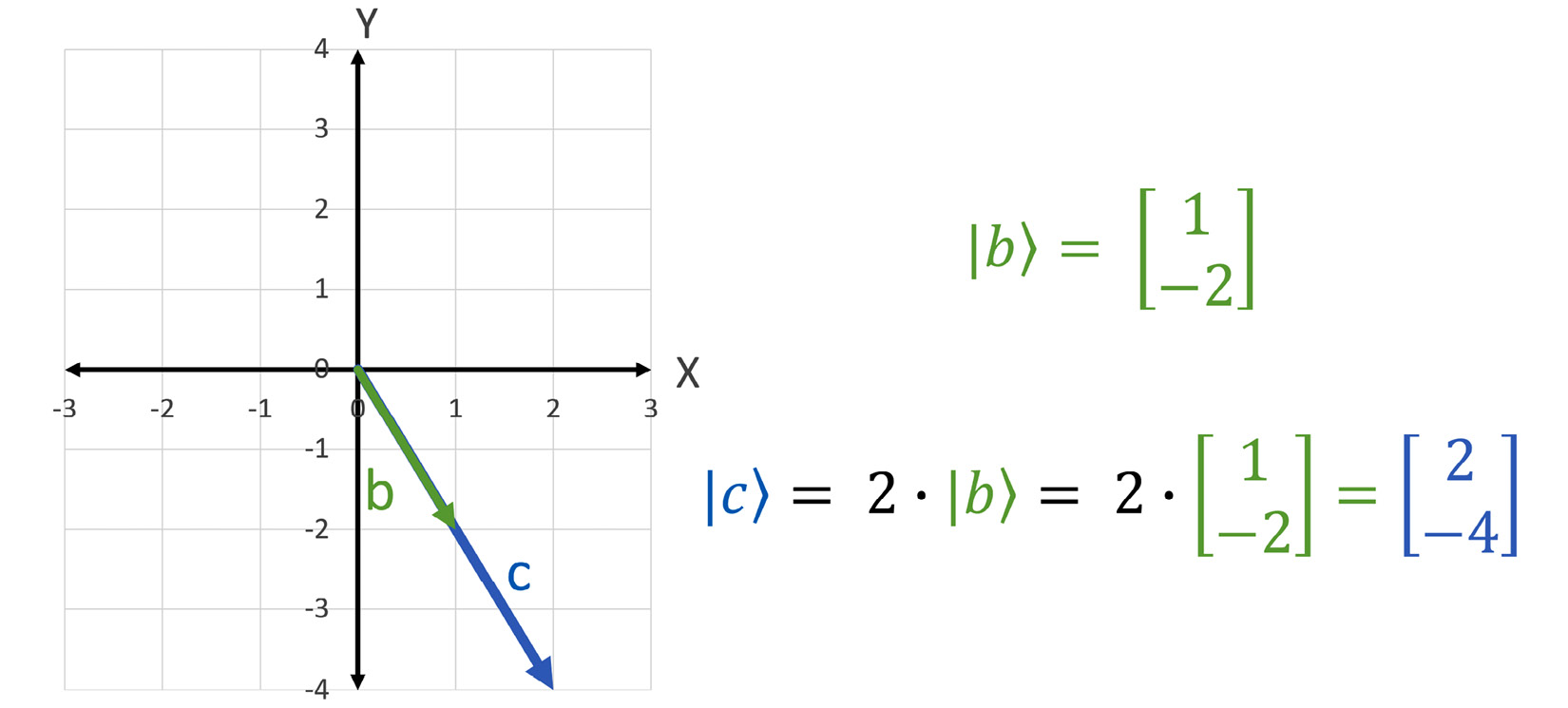
Figure 1.5 – Scalar multiplication

The vector |b⟩ is doubled or multiplied by two. Geometrically, we take the vector |b⟩ and scale its length by two while preserving its direction. Algebraically, we can just multiply the components of the vector by the number or scalar two.

Example

What is triple the vector |x⟩ shown here?

The solution is:

Exercise 2

• What is 4|x⟩?
• What is -2|x⟩?

Once we have established that we can add our vectors and multiply them by scalars, we can start to talk about linear combinations. Linear combinations are just the scaling and addition of vectors to form new vectors. Let's start with our two vectors we have been working with the whole time, |a⟩ and |b⟩. I want to scale my vector |a⟩ by two to get a new vector |c⟩, as shown in the following screenshot:

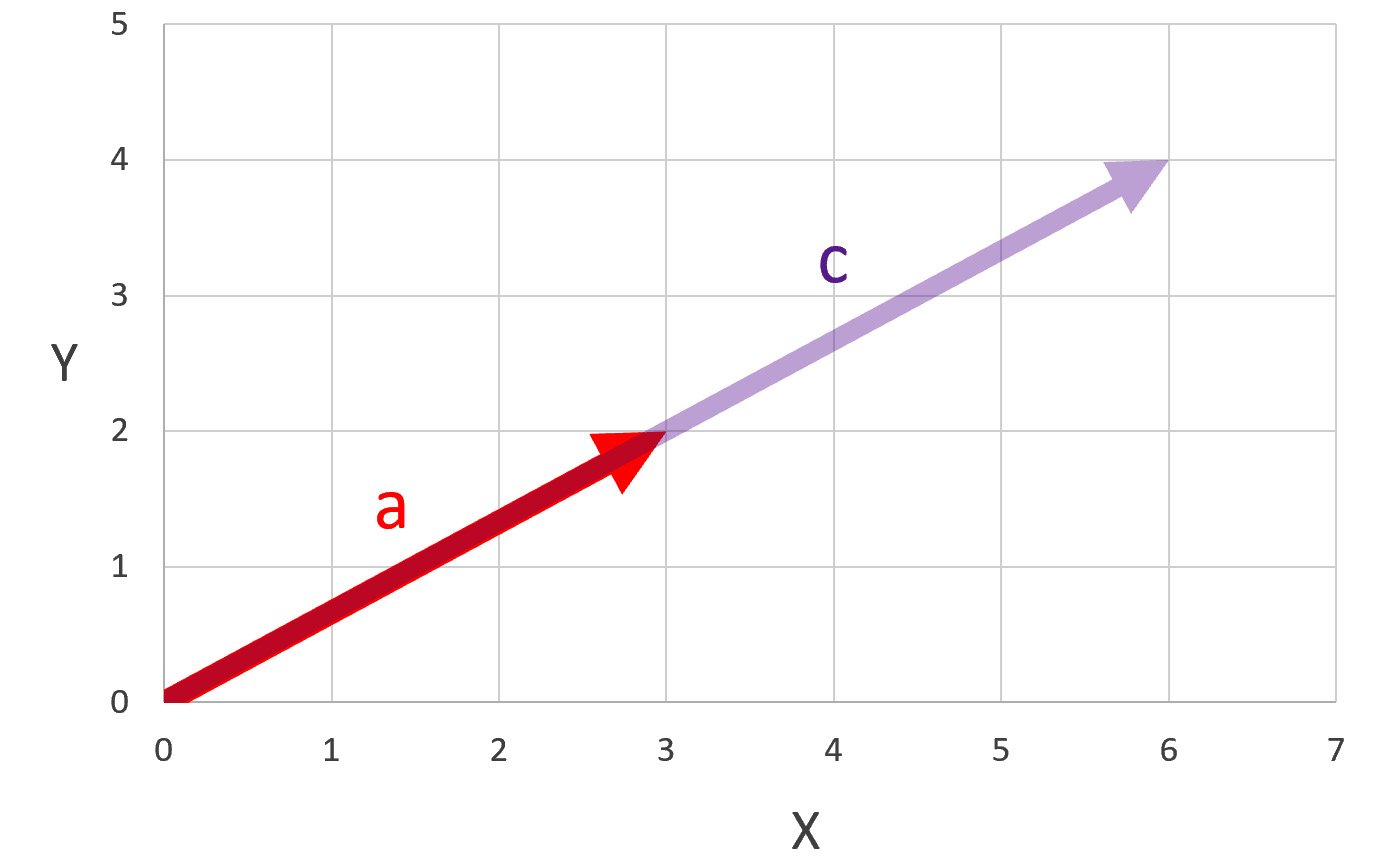
Figure 1.6 – |a⟩ scaled by two to produce |c⟩

As we have said, we can do this algebraically as well, as the following equation shows:

Then, I want to take my vector |b⟩ and scale it by two to get a new vector, |d⟩, as shown in the following screenshot:

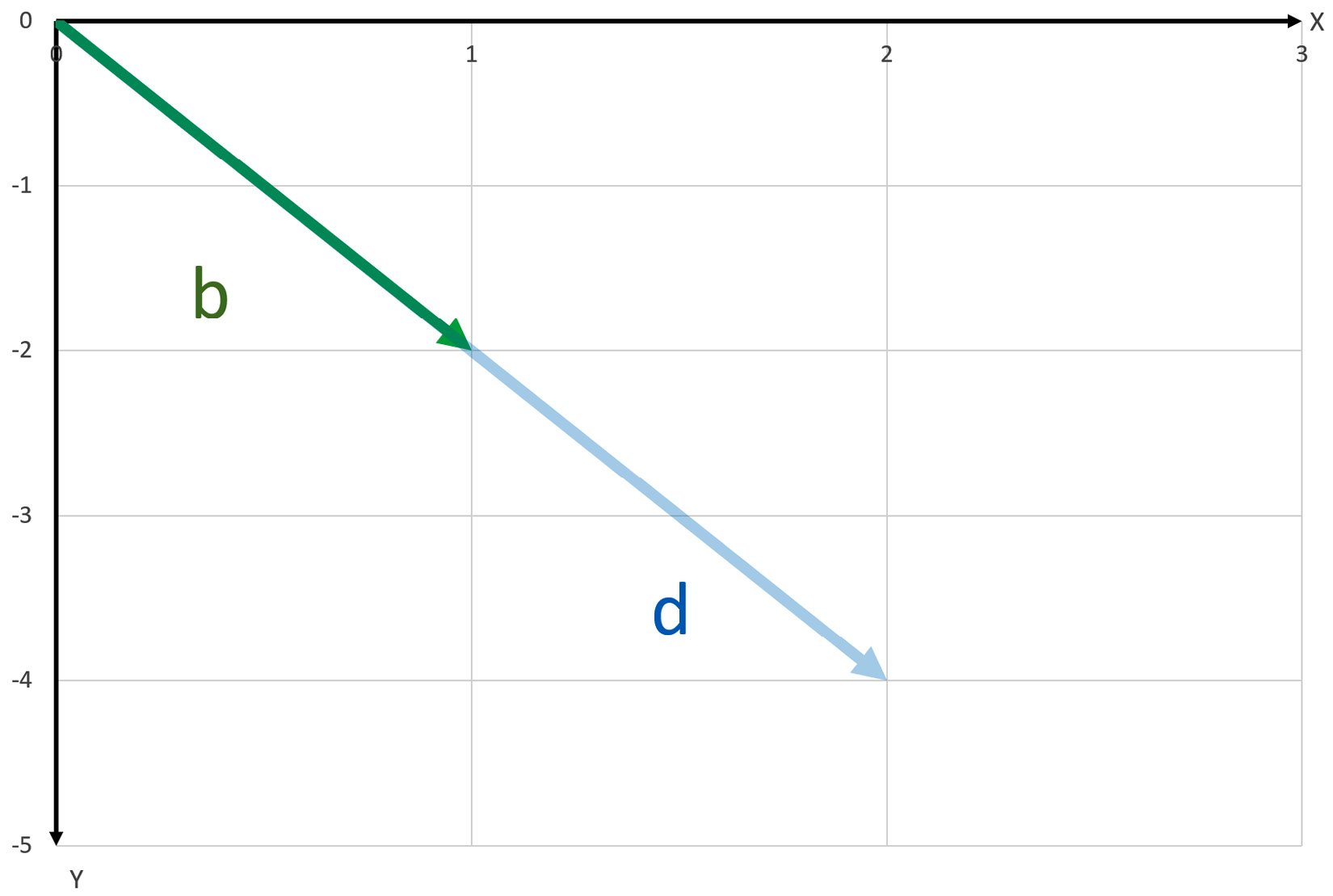
Figure 1.7 – |b⟩ scaled by two to produce |d⟩

So, now, we have a vector |c⟩ that is two times |a⟩, and a vector |d⟩ that is two times |b⟩:

Can I add these two new vectors, |c⟩ and |d⟩? Certainly! I will do that, but I will express |e⟩ as a linear combination of |a⟩ and |b⟩ in the following way:

Vector |e⟩ is a linear combination of vectors |a⟩ and |b⟩! Now, I can show this all geometrically, as follows:

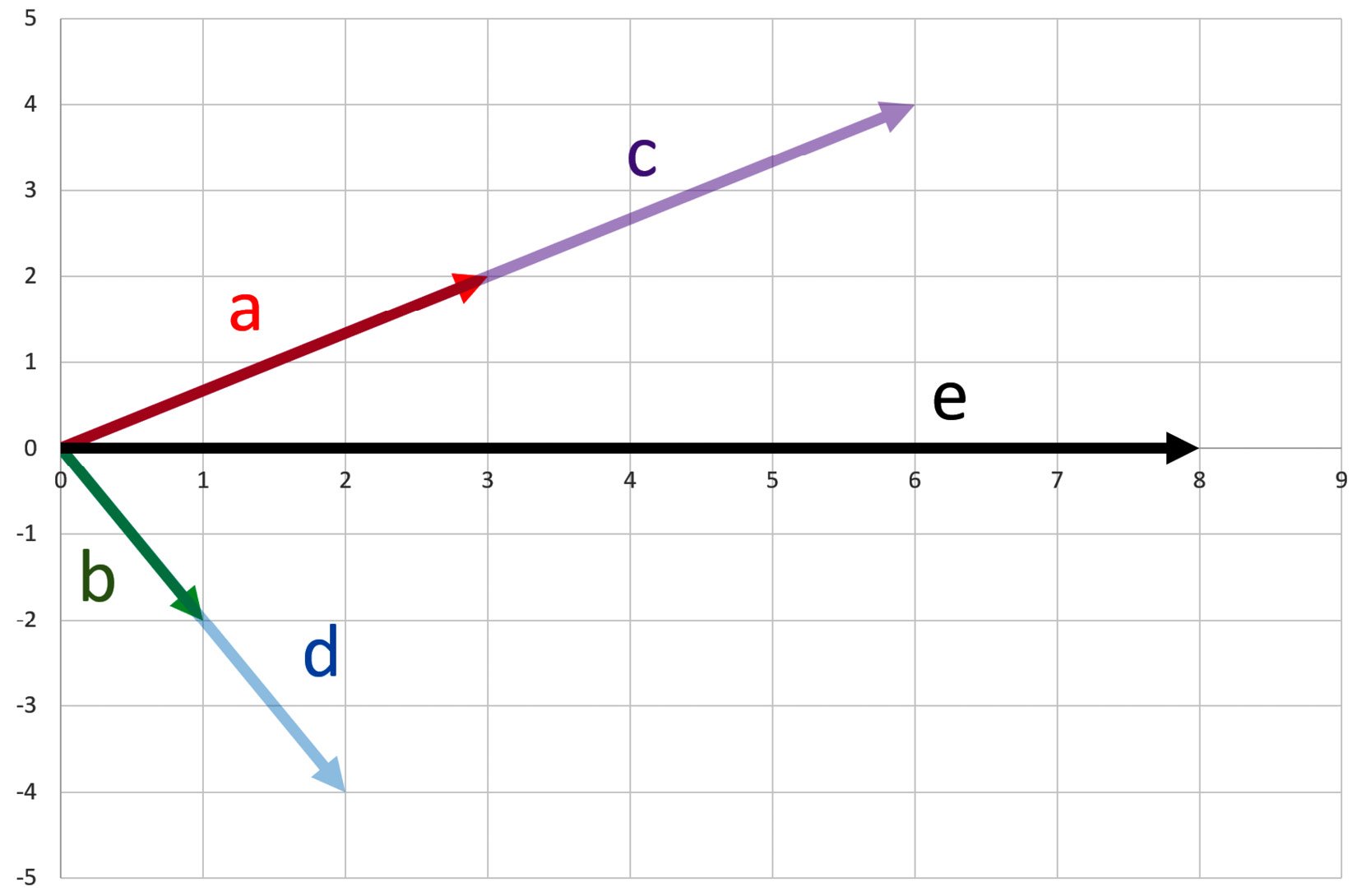
Figure 1.8 – Linear combination

This can also be represented in the following equation:

So, we now have a firm grasp on Euclidean vectors, the algebra you can perform with them, and the concept of a linear combination. We will use that in this next section to describe a quantum phenomenon called superposition.

Superposition can be a very imposing term, so before we delve into it, let's take a step back and talk about the computers we use today. In quantum computing, we call these computers "classical computers" to distinguish them from quantum computers. Classical computers use binary digits—or bits, for short—to store ones and zeros. These ones and zeros can represent anything, from truth values to characters to pixel values on a screen! They are physically implemented using any two-state device such as an electrical switch that is either on or off.

A quantum bit, or qubit for short, is the analogous building block of quantum computers. They are implemented by anything that demonstrates quantum phenomena, which means they are very, very small. In the following screenshot, we show how a property of an electron—namely spin—can be used to represent a one or zero of a qubit:

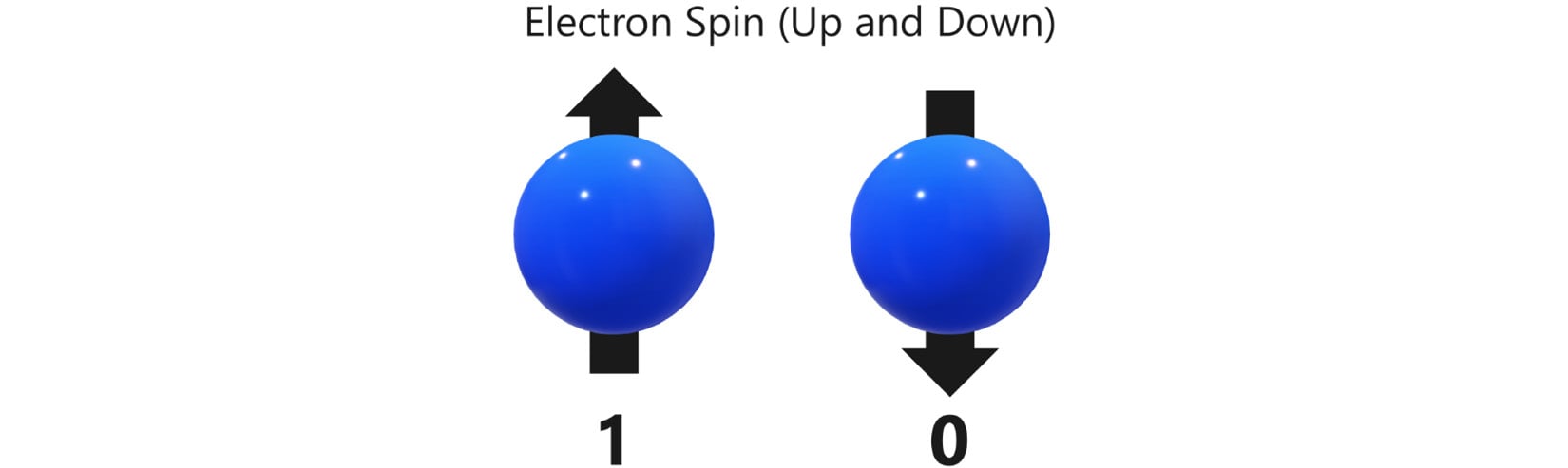
Figure 1.9 – Pair of electrons with a spin labeled 1 and 0

Physicists use mathematics to model quantum phenomena, and guess what they use to model the state of a quantum particle? That's right! Vectors! Quantum computer scientists have taken two of these states and labeled them as the canonical one and zero for qubits. They are shown in the following screenshot:

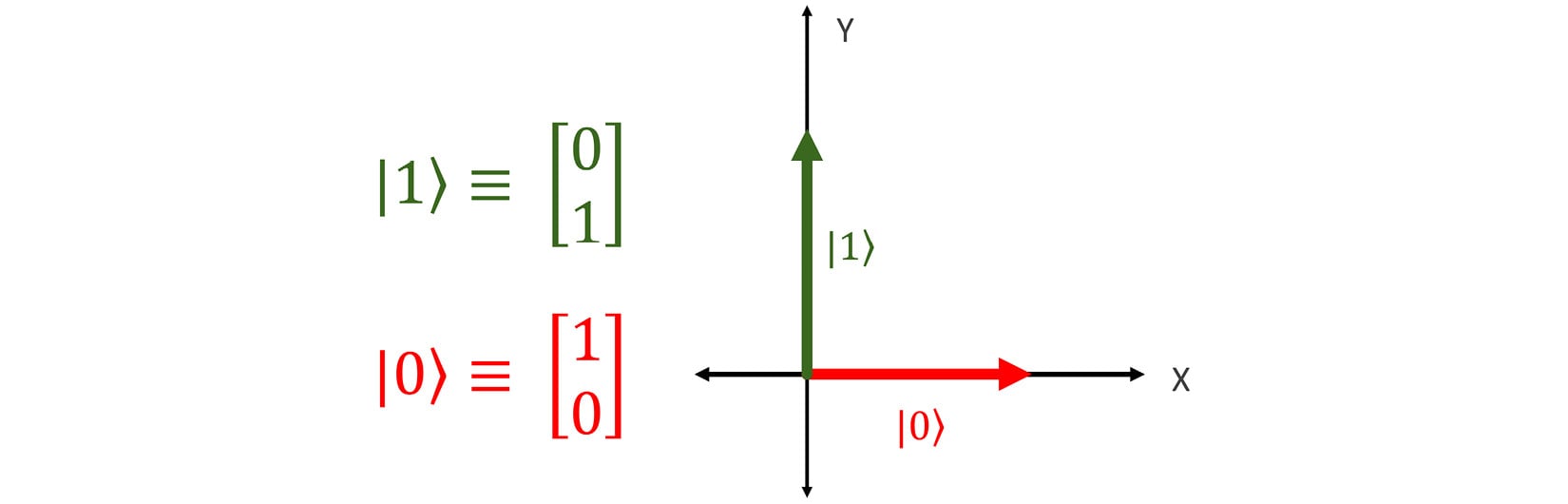
Figure 1.10 – Zero and one states

As you can see, the zero and one states are just vectors on the x and y axes with a length of one unit each. When you combine a lot of ones and zeros in classical computing, wonderful, complex things can be done. The same is true of the zero and one state of qubits in quantum computing.

Greek Letters

Mathematicians and physicists love Greek letters, and they have found their way into quantum computing in several places. The Greek letter "Psi", ψ, is often used to represent the state of a qubit. The Greek letters "alpha", α, and "beta", β, are used to represent numbers or scalars.

While qubits can represent a one or a zero, they have a superpower in that they can represent a combination of a zero and one as well! "How?" you might ask. Well, this is where superposition comes in. Understanding it is actually quite simple from a mathematical standpoint. In fact, you already know what it is! It's just a fancy way of saying that a qubit is in a linear combination of states.

If you recall, we defined the vector |e⟩ as a linear combination of the aforementioned |a⟩ and |b⟩, like so:

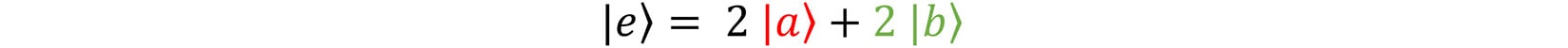
Figure 1.11 – Definition of |e⟩

If we replace those letters and numbers with the Greek letters and the zero and one states we just introduced, we get an equation like this:

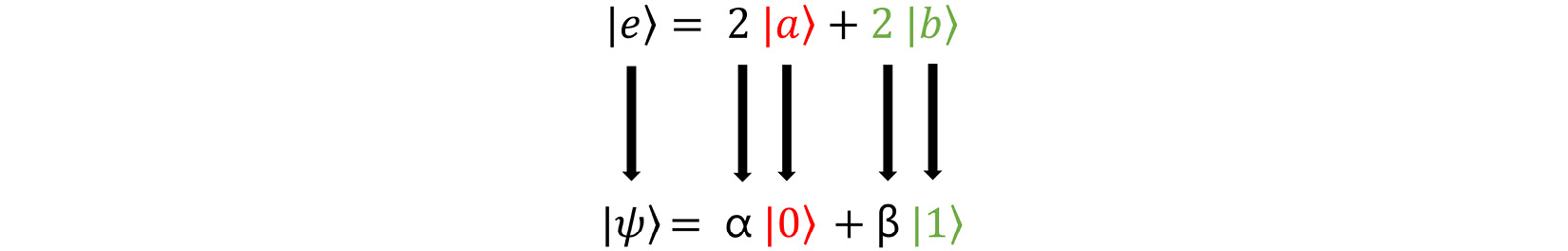
Figure 1.12 – Greek letters being transposed onto a linear combination equation

The bottom equation represents a qubit in the state |ψ⟩, which is a superposition of the states zero and one! You now know what superposition is mathematically! This, by the way, is the only way that counts because math is the language of physics and, therefore, quantum computing.

Measurement

But wait—there's more! With only the simple mathematics you have acquired so far, you also get a look at the weird act of measuring qubits. The scalars α and β shown previously play a crucial role when measuring qubits. In fact, if we were to set this qubit up in the state |ψ⟩ an infinite number of times, when we measured it for a zero or a one, |α|² would give us the probability of getting a zero, and |β|² would give us the probability of getting a one. Pretty cool, eh!?!

So, here is a question. For the qubit state |ψ⟩ in the following equation, what is the probability of getting a zero or a one when we measure it?

Well, if we said |α|² gives us the probability of getting a zero, then the answer would look like this:

This tells us that one half or 50% of the time when we measure for a zero or a one, we will get a zero. We can do the same exact math for β and derive that the other half of the time when we measure, we will get a one. The state |ψ⟩ shown previously represents the proverbial coin being flipped into the air and landing heads for a one and tails for a zero.

In a short amount of time, we have developed enough mathematics to explain superposition and its effects on measurement. We did this by introducing Euclidean vectors and the operations of addition and scalar multiplication upon them. Putting these operations together, we were able to get a definition for a linear combination and then apply that definition to what is termed superposition. In the end, we could use all of this to predict the probability of getting a zero or one when measuring a qubit.

In the next chapter, we will introduce the concept of a matrix and use it to manipulate qubits!

History (Optional)

Euclidean vectors are named after the Greek mathematician Euclid circa 300 BC. In his book, The Elements, he puts together postulates and theories from other Greek mathematicians, including Pythagoras, that defined Euclidean geometry. The book was a required textbook for math students for over 2,000 years.

Figure 1.13 – Euclid with other Greek mathematicians in Raphael's School of Athens

Exercise 1

a)

b)

c)

Exercise 2

a)

b)