Building Machine Learning Projects with TensorFlow

Tensor ranks represent the dimensional aspect of a tensor, but is not the same as a matrix rank. It represents the quantity of dimensions in which the tensor lives, and is not a precise measure of the extension of the tensor in rows/columns or spatial equivalents.

A rank one tensor is the equivalent of a vector, and a rank one tensor is a matrix. For a rank two tensor you can access any element with the syntax t[i, j]. For a rank three tensor you would need to address an element with t[i, j, k], and so on.

In the following example, we will create a tensor, and access one of its components:

>>> import tensorflow as tf 
>>> tens1 = tf.constant([[[1,2],[2,3]],[[3,4],[5,6]]]) 
>>> print sess.run(tens1)[1,1,0] 
5 

This is a tensor of rank three, because in each element of the containing matrix, there is a vector element:

The TensorFlow documentation uses three notational conventions to describe tensor dimensionality: rank, shape, and dimension number. The following table shows how these relate to one another:

In the following example, we create a sample rank three tensor, and print the shape of it:

In addition to dimensionality, tensors have a fixed data type. You can assign any one of the following data types to a tensor:

TensorFlow is interoperable with numpy, and normally the eval() function calls will return a numpy object, ready to be worked with the standard numerical tools.

In this example, we build two numpy arrays, and convert them to tensors:

import tensorflow as tf #we import tensorflow 
import numpy as np   #we import numpy 
sess = tf.Session() #start a new Session Object 
x_data = np.array([[1.,2.,3.], 
[3.,2.,6.]]) # 2x3 matrix 
x = tf.convert_to_tensor(x_data, dtype=tf.float32) #Finally, we create the tensor, starting from the fload 3x matrix 

To initialize a variable, simply call the Variable object constructor, with a tensor as a parameter.

In this example, we initialize some variables with an array of 1000 zeros:

b = tf.Variable(tf.zeros([1000])) 

Protocol buffers are a language-neutral, platform-neutral, extensible mechanism for serializing structured data. You define the data structure first, and then you can use specialized generated code to read and write it with a variety of languages.

In this example we will build a very simple data flow graph, and observe an overview of the generated protobuffer file:

import tensorflow as tf 
g = tf.Graph() 
with g.as_default(): 
import tensorflow as tf 
sess = tf.Session() 
W_m = tf.Variable(tf.zeros([10, 5])) 
x_v = tf.placeholder(tf.float32, [None, 10]) 
result = tf.matmul(x_v, W_m) 
print g.as_graph_def() 

The generated protobuffer (summarized) reads:

node {
  name: "zeros"
  op: "Const"
  attr {
    key: "dtype"
    value {
      type: DT_FLOAT
    }
  }
  attr {
    key: "value"
    value {
      tensor {
        dtype: DT_FLOAT
        tensor_shape {
          dim {
            size: 10
          }
          dim {
            size: 5
          }
        }
        float_val: 0.0
      }
    }
  }
}
...
node {
  name: "MatMul"
  op: "MatMul"
  input: "Placeholder"
  input: "Variable/read"
  attr {
    key: "T"
    value {
      type: DT_FLOAT
    }
  }
...
}
versions {
  producer: 8
}

Reduction is an operation that applies an operation across one of the tensor's dimensions, leaving it with one less dimension.

The supported operations include (with the same parameters) product, minimum, maximum, mean, all, any, and accumulate_n).

In [1]: import tensorflow as tf 
 
In [2]: sess = tf.InteractiveSession() 
In [3]: x = tf.constant([[1,  2, 3], 
...:                  [3,  2, 1], 
...:                  [-1,-2,-3]]) 
In [4]: 
 
In [4]: boolean_tensor = tf.constant([[True,  False, True], 
...:                  [False, False, True], 
...:                  [True, False, False]]) 
 
In [5]: tf.reduce_prod(x, reduction_indices=1).eval() # reduce prod 
Out[5]: array([ 6,  6, -6], dtype=int32) 
 
In [6]: tf.reduce_min(x, reduction_indices=1).eval() # reduce min 
Out[6]: array([ 1,  1, -3], dtype=int32) 
 
In [7]: tf.reduce_max(x, reduction_indices=1).eval() # reduce max 
Out[7]: array([ 3,  3, -1], dtype=int32) 
 
In [8]: tf.reduce_mean(x, reduction_indices=1).eval() # reduce mean 
Out[8]: array([ 2,  2, -2], dtype=int32) 
 
In [9]: tf.reduce_all(boolean_tensor, reduction_indices=1).eval() # reduce all 
Out[9]: array([False, False, False], dtype=bool) 
 
In [10]: tf.reduce_any(boolean_tensor, reduction_indices=1).eval() # reduce any 
Out[10]: array([ True,  True,  True], dtype=bool) 

Tensor segmentation is a process in which one of the dimensions is reduced, and the resulting elements are determined by an index row. If some elements in the row are repeated, the corresponding index goes to the value in it, and the operation is applied between the indexes with repeated indexes.

The index array size should be the same as the size of dimension 0 of the index array, and they must increase by one.

Segmentation explanation (redo)

In [1]: import tensorflow as tf 
In [2]: sess = tf.InteractiveSession() 
In [3]: seg_ids = tf.constant([0,1,1,2,2]); # Group indexes : 0|1,2|3,4 
In [4]: tens1 = tf.constant([[2, 5, 3, -5], 
...:                     [0, 3,-2,  5], 
...:                     [4, 3, 5,  3], 
...:                     [6, 1, 4,  0], 
...:                     [6, 1, 4,  0]])  # A sample constant matrix 
 
In [5]: tf.segment_sum(tens1, seg_ids).eval()   # Sum segmentation 
Out[5]: 
array([[ 2,  5,  3, -5], 
[ 4,  6,  3,  8], 
[12,  2,  8,  0]], dtype=int32) 
 
In [6]: tf.segment_prod(tens1, seg_ids).eval() # Product segmentation 
Out[6]: 
array([[  2,   5,   3,  -5], 
[  0,   9, -10,  15], 
[ 36,   1,  16,   0]], dtype=int32) 
 
In [7]: tf.segment_min(tens1, seg_ids).eval() # minimun value goes to group 
Out[7]: 
array([[ 2,  5,  3, -5], 
[ 0,  3, -2,  3], 
[ 6,  1,  4,  0]], dtype=int32) 
 
In [8]: tf.segment_max(tens1, seg_ids).eval() # maximum value goes to group 
Out[8]: 
array([[ 2,  5,  3, -5], 
[ 4,  3,  5,  5], 
[ 6,  1,  4,  0]], dtype=int32) 
 
In [9]: tf.segment_mean(tens1, seg_ids).eval() # mean value goes to group 
Out[9]: 
array([[ 2,  5,  3, -5], 
[ 2,  3,  1,  4], 
[ 6,  1,  4,  0]], dtype=int32) 

In order to extract and merge useful information from big datasets, the slicing and joining methods allow you to consolidate the required column information without having to occupy memory space with nonspecific information.

In the following examples, we'll extract matrix slices, split them, add padding, and pack and unpack rows:

In [1]: import tensorflow as tf 
In [2]: sess = tf.InteractiveSession() 
In [3]: t_matrix = tf.constant([[1,2,3], 
...:                         [4,5,6], 
...:                         [7,8,9]]) 
In [4]: t_array = tf.constant([1,2,3,4,9,8,6,5]) 
In [5]: t_array2= tf.constant([2,3,4,5,6,7,8,9]) 
 
In [6]: tf.slice(t_matrix, [1, 1], [2,2]).eval() # cutting an slice 
Out[6]: 
array([[5, 6], 
[8, 9]], dtype=int32) 
 
In [7]: tf.split(0, 2, t_array) # splitting the array in two 
Out[7]: 
[<tf.Tensor 'split:0' shape=(4,) dtype=int32>, 
<tf.Tensor 'split:1' shape=(4,) dtype=int32>] 
 
In [8]: tf.tile([1,2],[3]).eval() # tiling this little tensor 3 times 
Out[8]: array([1, 2, 1, 2, 1, 2], dtype=int32) 
 
In [9]: tf.pad(t_matrix, [[0,1],[2,1]]).eval() # padding 
Out[9]: 
array([[0, 0, 1, 2, 3, 0], 
[0, 0, 4, 5, 6, 0], 
[0, 0, 7, 8, 9, 0], 
[0, 0, 0, 0, 0, 0]], dtype=int32) 
 
In [10]: tf.concat(0, [t_array, t_array2]).eval() #concatenating list 
Out[10]: array([1, 2, 3, 4, 9, 8, 6, 5, 2, 3, 4, 5, 6, 7, 8, 9], dtype=int32) 
 
In [11]: tf.pack([t_array, t_array2]).eval() # packing 
Out[11]: 
array([[1, 2, 3, 4, 9, 8, 6, 5], 
[2, 3, 4, 5, 6, 7, 8, 9]], dtype=int32) 
 
In [12]: sess.run(tf.unpack(t_matrix)) # Unpacking, we need the run method to view the tensors 
Out[12]: 
[array([1, 2, 3], dtype=int32), 
array([4, 5, 6], dtype=int32), 
array([7, 8, 9], dtype=int32)] 
 
In [13]: tf.reverse(t_matrix, [False,True]).eval() # Reverse matrix 
Out[13]: 
array([[3, 2, 1], 
[6, 5, 4], 
[9, 8, 7]], dtype=int32) 

To invoke TensorBoard, the command line is:

All Summaries in a TensorFlow Session are written by a SummaryWriter object. The main method to call is:

tf.train.SummaryWriter.__init__(logdir, graph_def=None) 

This command will create a SummaryWriter and an event file, in the path of the parameter.

The constructor of the the SummaryWriter will create a new event file in logdir. This event file will contain Event type protocol buffers constructed when you call one of the following functions: add_summary(), add_session_log(), add_event(), or add_graph().

If you pass a graph_def protocol buffer to the constructor, it is added to the event file. (This is equivalent to calling add_graph() later).

When you run TensorBoard, it will read the graph definition from the file and display it graphically so you can interact with it.

First, create the TensorFlow graph that you'd like to collect summary data from and decide which nodes you would like to annotate with summary operations.

Operations in TensorFlow don't do anything until you run them, or an operation that depends on their output. And the summary nodes that we've just created are peripheral to your graph: none of the ops you are currently running depend on them. So, to generate summaries, we need to run all of these summary nodes. Managing them manually would be tedious, so use tf.merge_all_summaries to combine them into a single op that generates all the summary data.

Then, you can just run the merged summary op, which will generate a serialized Summary protobuf object with all of your summary data at a given step. Finally, to write this summary data to disk, pass the Summary protobuf to a tf.train.SummaryWriter.

The SummaryWriter takes a logdir in its constructor, this logdir is quite important, it's the directory where all of the events will be written out. Also, the SummaryWriter can optionally take a GraphDef in its constructor. If it receives one, then TensorBoard will visualize your graph as well.

Now that you've modified your graph and have a SummaryWriter, you're ready to start running your network! If you want, you could run the merged summary op every single step, and record a ton of training data. That's likely to be more data than you need, though. Instead, consider running the merged summary op every n steps.

This is a list of the different Summary types, and the parameters employed on its construction:

These are special functions, that are used to merge the values of different operations, be it a collection of summaries, or all summaries in a graph:

Finally, as one last aid to legibility, the visualization uses special icons for constants and summary nodes. To summarize, here's a table of node symbols:

Symbol	Meaning
	High-level node representing a name scope. Double-click to expand a high-level node.
	Sequence of numbered nodes that are not connected to each other.
	Sequence of numbered nodes that are connected to each other.
	An individual operation node.
	A constant.
	A summary node.
	Edge showing the data flow between operations.
	Edge showing the control dependency between operations.
	A reference edge showing that the outgoing operation node can mutate the incoming tensor.

Navigate the graph by panning and zooming. Click and drag to pan, and use a scroll gesture to zoom. Double-click on a node, or click on its + button, to expand a name scope that represents a group of operations. To easily keep track of the current viewpoint when zooming and panning, there is a minimap in the bottom-right corner:

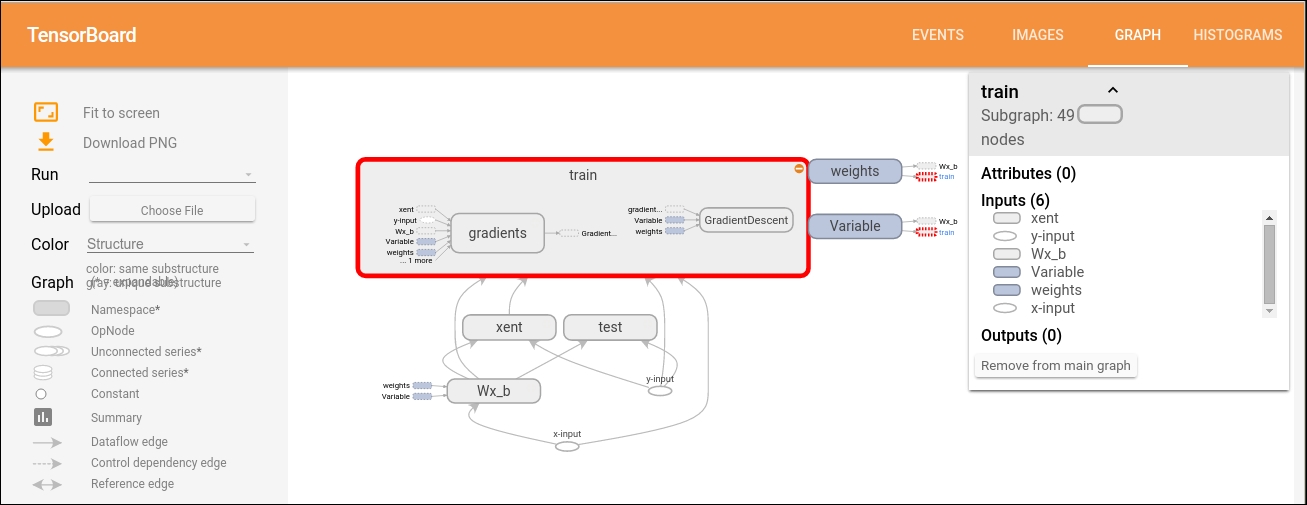
Openflow with one expanded operations group and legends

To close an open node, double-click it again or click its - button. You can also click once to select a node. It will turn a darker color, and details about it and the nodes it connects to will appear in the info card in the upper-right corner of the visualization.

Selection can also be helpful in understanding high-degree nodes. Select any high-degree node, and the corresponding node icons for its other connections will be selected as well. This makes it easy, for example, to see which nodes are being saved and which aren't.

Clicking on a node name in the info card will select it. If necessary, the viewpoint will automatically pan so that the node is visible.

Finally, you can choose two color schemes for your graph, using the color menu above the legend. The default Structure View shows the structure: when two high-level nodes have the same structure, they appear in the same color of the rainbow. Uniquely structured nodes are gray. There's a second view, which shows what device the different operations run on. Name scopes are colored proportionally, to the fraction of devices for the operations inside them.

For reading the well-known CSV format, TensorFlow has its own methods. In comparison with other libraries, such as pandas, the process to read a simple CSV file is somewhat more complicated.

The reading of a CSV file requires a couple of the previous steps. First, we must create a filename queue object with the list of files we'll be using, and then create a TextLineReader. With this line reader, the remaining operation will be to decode the CSV columns, and save it on tensors. If we want to mix homogeneous data together, the pack method will work.

The Iris dataset

The Iris flower dataset or Fisher's Iris dataset is a well know benchmark for classification problems. It's a multivariate data set introduced by Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis.

The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica, and Iris versicolor). Four features were measured in each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other. (You'll be able to get the .csv file for this dataset in the code bundle of the book.)

In order to read the CSV file, you will have to download it and put it in the same directory as where the Python executable is running.

In the following code sample, we'll be reading and printing the first five records from the well-known Iris database:

import tensorflow as tf 
sess = tf.Session() 
filename_queue = tf.train.string_input_producer( 
tf.train.match_filenames_once("./*.csv"), 
shuffle=True) 
reader = tf.TextLineReader(skip_header_lines=1) 
key, value = reader.read(filename_queue) 
record_defaults = [[0.], [0.], [0.], [0.], [""]] 
col1, col2, col3, col4, col5 = tf.decode_csv(value, record_defaults=record_defaults)  # Convert CSV records to tensors. Each column maps to one tensor. 
features = tf.pack([col1, col2, col3, col4]) 
 
tf.initialize_all_variables().run(session=sess) 
coord = tf.train.Coordinator() 
threads = tf.train.start_queue_runners(coord=coord, sess=sess) 
 
for iteration in range(0, 5):
 example = sess.run([features])
 print(example)
 coord.request_stop()
 coord.join(threads)
 

And this is how the output would look:

TensorFlow allows importing data from image formats, it will really be useful for importing custom image inputs for image oriented models.The accepted image formats will be JPG and PNG, and the internal representation will be uint8 tensors, one rank two tensor for each image channel:

Sample image to be read

In this example, we will load a sample image and apply some additional processing to it, saving the resulting images in separate files:

import tensorflow as tf 
sess = tf.Session() 
filename_queue = tf.train.string_input_producer(tf.train.match_filenames_once("./blue_jay.jpg")) 
reader = tf.WholeFileReader() 
key, value = reader.read(filename_queue) 
image=tf.image.decode_jpeg(value) 
flipImageUpDown=tf.image.encode_jpeg(tf.image.flip_up_down(image)) 
flipImageLeftRight=tf.image.encode_jpeg(tf.image.flip_left_right(image)) 
tf.initialize_all_variables().run(session=sess) 
coord = tf.train.Coordinator() 
threads = tf.train.start_queue_runners(coord=coord, sess=sess) 
example = sess.run(flipImageLeftRight) 
print example 
file=open ("flippedUpDown.jpg", "wb+") 
file.write (flipImageUpDown.eval(session=sess)) 
file.close() 
file=open ("flippedLeftRight.jpg", "wb+") 
file.write (flipImageLeftRight.eval(session=sess)) 
file.close() 

The print example line will show a line-by-line summary of the RGB values in the image:

The final images will look like:

Original and altered images compared (flipUpDown and flipLeftRight)

Another approach is to convert the arbitrary data you have, into the official format. This approach makes it easier to mix and match data sets and network architectures.

You can write a little program that gets your data, stuffs it in an example protocol buffer, serializes the protocol buffer to a string, and then writes the string to a TFRecords file using the tf.python_io.TFRecordWriter class.

To read a file of TFRecords, use tf.TFRecordReader with the tf.parse_single_example decoder. The parse_single_example op decodes the example protocol buffers into tensors.