Understanding theoretical computer science

While you don’t need to be a master mathematician to love computer science, these two subjects are intrinsically tied. Computer science, particularly programming, uses algebraic algorithms. We will explore algorithms in depth later on, but again, the important point here is that they are mathematical. The logical processes stem from the philosophical nature and history of mathematics. Now, if mathematical topics are not to your liking, don’t despair. The logical processes needed to become a programmer and developer can be used without you having to learn higher mathematics. Knowing higher mathematics just simplifies some concepts for those who have that background.

Theoretical computer science includes multiple theories and topics. Some of these topics and theories are listed as follows, but keep in mind that other topics are also included in theoretical computer science that may not be discussed in this book. A short description and explanation of each of the theories or terms listed here have been included for you to review:

• Algorithms
• Coding theory
• Computational biology
• Data structures
• Cryptography
• Information theory
• Machine learning
• Automata theory
• Formal language theory
• Symbolic computation
• Computational geometry
• Computational number theory

We will look at the aforementioned theories in the following sections.

Algorithms

An algorithm is a set of instructions that a computer can read. Algorithms provide rules or instructions in a way in which a computer can logically process the information provided as input and create an output. In most books, you are introduced to the algorithm and programming by creating a Hello World! program. I won’t make this book the exception.

In Python, the code would require that we print the message to the screen. Because the Python language is easy to learn and read, many, if not most, of the code strives to be logical. So, to print a message to the screen, we can use the print() command. Here is the code we’d use:

print("Hello world!")

Similarly, we could use the following code:

print('Hello world!")

Python reads both " and ' as the same thing when it comes to strings.

The result of the preceding code looks like this when we run the algorithm:

Figure 1.3 – The Hello World! Python program

Note

Don’t worry – we’ll discuss the Python programming language later in Chapter 2, Elements of Computational Thinking, and in more depth in Part 2, Applying Python and Computational Thinking, starting with Chapter 9, Introduction to Python, as well.

While lengthy, discussing algorithms is critically important to this book and your progression with Python. Consequently, we will be covering this in-depth exploration of algorithms in Chapter 2, Elements of Computational Thinking, and Chapter 3, Understanding Algorithms and Algorithmic Thinking, since algorithms are a key element of the computational thinking process.

Important note

Chapter 2, Elements of Computational Thinking, will focus on the computational thinking process itself, which has four elements: decomposition, pattern recognition, pattern generalization and abstraction, and algorithm design. As you can see, the last element is algorithm design, so we will need to get more acquainted with what an algorithm is and how we can create one so that you can then implement and design algorithms when solving problems with Python. Chapter 3, Understanding Algorithms and Algorithmic Thinking, will focus on a deeper understanding of algorithms and introduce you to the design process.

We’ll look at coding theory next.

Coding theory

Coding theory is also sometimes known as algebraic coding theory. When working with code and coding theory, three major areas are studied: data compression, error correction, and cryptography. We will cover these in more detail in the following sections.

Data compression

The importance of data compression cannot be understated. Data compression allows us to store the maximum amount of information possible while taking up the least amount of space. In other words, data compression is the process of using the fewest number of bits to store the data.

Important note

Remember that a bit is the smallest unit of data you can find in a computer – that is, a 0 or a 1. A group of 8 bits is called a byte. We use bytes as a unit of measurement for the size of the memory of a computer or storage device, such as a memory card or external drive, and more.

As our technology and storage capacities have grown and improved, our ability to store additional data has as well. Historically, computers had kilobytes or megabytes of storage when they were first introduced into households, but at the time of writing, they now have gigabytes and terabytes worth of storage. The conversions for each of these storage units are shown here:

Figure 1.4 – Byte conversions

If you look for information online, you may find that some sources state that there are 1,024 gigabytes in a terabyte. That is a binary conversion. In the decimal system or base-10 system, there are 1,000 gigabytes per terabyte. To understand conversion better, it is important to understand the prefixes that apply to the base-10 system and the prefixes that apply to the binary system:

Base-10 Prefixes	Value	Binary Prefixes	Value
kilo	1,000	kibi	1,024
mega	1,0002	mebi	1,0242
giga	1,0003	gibi	1,0243
tera	1,0004	tebi	1,0244
peta	1,0005	pebi	1,0245
exa	1,0006	exbi	1,0246
zetta	1,0007	zebi	1,0247
yotta	1,0008	yobi	1,0248

Table 1.2 – Base-10 and binary prefixes with values

As mentioned, the goal is always to use the least amount of bits for the largest amount of data possible. Therefore, we compress, or reduce, the size of data to use less storage.

So, why is data compression so important? Let’s go back in time to 2000. Here, a laptop computer on sale for about $1,000 had about 64 MB of Random Access Memory (RAM) and 6 GB of hard drive memory. A photograph on our digital phones takes anywhere from 2 to 5 megabytes of memory when we use its actual size. That means our computers couldn’t store many (and in some cases, any) of the modern pictures we take now. Data compression advances allow us to store more memory, create better games and applications, and much more as we can have better graphics and additional information or code without having to worry as much about the amount of memory they use.

Error correction

In computer science, errors are a fact of life. We make mistakes in our processes, our algorithms, our designs, and everything in between. Error correction, also known as error handling, is the process a computer goes through to automatically correct an error or multiple errors, which happens when digital data is transmitted incorrectly.

An Error Correction Code (ECC) can help us analyze data transmissions. ECC locates and corrects transmission errors. In computers, ECC is built into a storage space that can identify common internal data corruption problems. For example, ECC can help read broken codes, such as a missing piece of a Quick Response (QR) code. An example of ECC is hamming codes. A hamming code is a binary linear code that can detect up to two-bit errors. This means that up to two bits of data can be lost or corrupted during transmission, and the receiver will know that an error occurred, or be able to reconstruct the original data with no errors.

Important note

Hamming codes are named after Richard Wesley Hamming, who discovered them in 1950. Hamming was a mathematician who worked with coding related to telecommunications and computer engineering.

Another type of ECC is a parity bit. A parity bit checks the status of data and determines whether any data has been lost or overwritten. Error correction is important for all software that’s developed because any updates, changes, or upgrades can lead to the entire program or parts of the program or software being corrupted.

Cryptography

Cryptography is used in computer science to hide code. In cryptography, information or data is written so that it can’t be read by anyone other than the intended recipient of the message. In simple terms, cryptography takes readable text or information and converts it into unreadable text or information.

When we think about cryptography now, we tend to think of encryption of data. Coders encrypt data by converting it into code that cannot be seen by unauthorized users. However, cryptography has been around for centuries – that is, it pre-dates computers. Historically, the first uses of cryptography were found around 1900 BC in a tomb in Egypt. Atypical or unusual hieroglyphs were mixed with common hieroglyphs at various parts of the tomb.

The reason for these unusual hieroglyphs is unknown, but the messages were hidden from others with their use. Later on, cryptography would be used to communicate in secret by governments and spies, in times of war and peace. Nowadays, cryptography is used to encrypt data since our information exists in digital format, so protecting sensitive information, such as banking, demographic, or personal data, is important.

We will be exploring the various topics surrounding coding theory through some of the problems presented throughout this book.

Computational biology

Computational biology is the area of theoretical computer science that focuses on the study of biological data and bioinformatics. Bioinformatics is a science that allows us to collect biological data and analyze it. An example of bioinformatics is collecting and analyzing genetic codes. In the study of biology, large quantities of data is explored and recorded.

Studies can be wide-ranging in topics and interdisciplinary. For example, a genetic study may include data from an entire state, an entire race, or an entire country. Some areas within computational biology include molecules, cells, tissues, and organisms. Computational biology allows us to study the composition of these things, from the most basic level to the larger organism. Bioinformatics and computational biology provide a structure for experimental studies in these areas, create predictions and comparisons, and provide us with a way to develop and test theories.

Computational thinking and coding allow us to process that data and analyze it. In this book, the problems presented will allow us to explore ways in which we can use Python in conjunction with computational thinking to find solutions to complex problems, including those in computational biology.

Data structures

In coding theory, we use data structures to collect and organize data. The goal is to prepare the data so that we can perform operations efficiently and effectively. Data structures can be primitive or abstract. Software has built-in data structures, which are primitive, or we can define them using our programming language. A primitive data structure is predefined. Some primitive data structures include integers, characters (chars), and Boolean structures. Examples of abstract or user-defined data structures include arrays and two-dimensional arrays, stacks, trees and binary trees, linked lists, queues, and more.

User-defined data structures have different characteristics. For example, they can be linear or non-linear, homogeneous or non-homogeneous, and static or dynamic. If we need to arrange data in a linear sequence, we can use an array, which is a linear data structure. If our data is not linear, we can use non-linear data structures, such as graphs. When we have data that is of a similar type, we use homogeneous data structures.

Keep in mind that an array, for example, is both a linear and homogeneous data structure. Non-homogeneous or heterogeneous data structures have dissimilar data. An example of a non-homogeneous data structure a user can create is a class. The difference between a static and a dynamic data structure is that the size of a static structure is fixed, while a dynamic structure is flexible in size. To build a better understanding of data structures, we will explore them through problem-solving by using various computational thinking elements. We will revisit data structures very briefly at the end of this chapter since they relate to data types, which we will discuss shortly.

Information theory

Information theory is defined as a mathematical study that allows us to code information so that it can be transmitted through computer circuits or telecommunications channels. The information is transmitted through sequences that may contain symbols, impulses, and even radio signals.

In information theory, computer scientists study the quantification of information, data storage, and information communication. Information can be either analog or digital in information theory. Analog data refers to information represented by an analog signal. In turn, an analog signal is a continuous wave that changes over a given time. A digital signal displays data as binary – that is, as a discrete wave. We represent analog waves as sine waves and digital waves as square waves. The following graph shows a sine curve as a function of value over time:

Figure 1.5 – Analog signal

An analog signal is described by the key elements of a sine wave: amplitude, period, frequency, and phase shift:

• The amplitude is the height of the curve from its center. A sine curve repeats infinitely.
• The period refers to the length of one cycle of the sine curve – that is, the length of the curve before it starts to repeat.
• The frequency and the period of the sine curve have an inverse relationship:

frequency =  1 _ period

Concerning the inverse relationship, we can also say the following:

period =  1 _ frequency

• The phase shift of a sine curve is how much the curve shifts from 0. This is shown in the following graph:

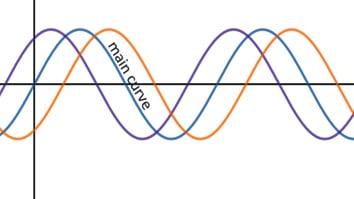
Figure 1.6 – Phase shift examples

In contrast, digital signal graphs look like bar graphs or histograms. They only have two data points, 0 or 1, so they look like boxy hills and valleys:

Figure 1.7 – Digital signal

Digital signals have finite sets of discrete data. A dataset is discrete in that it contains individual and distinct data points. For analog signals, the data is continuous and infinite. When working with computer science, both types of signals are important and useful. We will explore digital signals in some of the problems throughout the book, specifically in the problems presented in Chapter 17, Applied Computational Thinking Problems.

Automata theory

Automata theory is one of the most fascinating topics in theoretical computer science. It refers to the study of machines and how calculations can be completed reliably and efficiently. Automata theory involves the physical aspects of simple machines, as well as logical processing. So, what exactly are automata used for and how does it work?

Automata are devices that use predetermined conditions to respond to outside input. When you look at your thermostat, you’re working with an automata. You set the temperature you want and the thermostat reacts to an outside source to gather information and adjust the temperatures accordingly.

Another example of automata is surgical robots. These robots can improve the outcomes of surgeries for patients and are being improved upon constantly. Since the goal of automata theory is to make machines that are reliable and efficient, it is a critical piece in developing artificial intelligence and smart robotic machines such as surgical robots.

Formal language theory

Formal language theory is often tied to automata theory in computer science. Formal language theory involves studying the syntax, grammar, vocabulary, and everything else involving a formal language. In computer science, formal language refers to the logical processing and syntax of computer programming languages. Concerning automata, the machines process the formal language to perform the tasks or code provided for them.

Symbolic computation

Symbolic computation is a branch of computational mathematics that deals with computer algebra. The terms symbolic computation and computer algebra are sometimes used interchangeably. Some programming software and languages focus on the symbolic computations of mathematics formulas. Programs that use symbolic computation perform operations such as polynomial factorization, simplifying algebraic functions or expressions, finding the greatest common divisor of polynomials, and more.

In this book, we will use computer algebra and symbolic computation when solving some real-world problems. Python allows us to not only perform the mathematical computations that may be required for problems but also explore graphical representations or models that result from those computations. As we explore solutions to real-world problems, we will need to use various libraries or extensions of the Python programming language. More on that will be provided in Part 2, Applying Python and Computational Thinking, of this book, where we will explore the Python programming language in greater detail.

Computational geometry

Like symbolic computation, computational geometry lives in the branch of computer science that deals with computational mathematics. The algorithms we study in computational geometry are those that can be expressed with geometry. The data is analyzed via geometric figures, geometric analysis, data structures that follow geometric patterns, and more. The input and output of problems that require computational geometry are geometric.

When thinking of geometry, we often revert to the figures we mostly associate with that branch of mathematics, such as polygons, triangles, and circles. That said, when we look at computational geometry, some of the algorithms are those that can be expressed by points, lines, other geometric figures, or those that follow a geometric pattern. Triangulation falls under this branch of computer science.

Data triangulation is important for applications such as optical 3D measuring systems. We triangulate GPS signals to locate a phone, for example, which is used in law enforcement.

There are many uses of triangulation in modern times, some of which we’ll explore through real and relevant problems throughout this book.

Computational number theory

Number theory is a branch of mathematics that studies integers and their properties. So, computational number theory involves studying algorithms that are used to solve problems in number theory. Part of the study of number theory is primality testing.

Algorithms that are created to determine whether input or output is prime are used for many purposes. One of the most critically important uses and applications of primality testing and number theory is for encryption purposes. As our lives have moved to saving everything electronically, our most personal information, such as banking information, family information, and even social security numbers, lives in some code or algorithm. It is important to encrypt such information so that others cannot use or access it. Computational number theory and cryptography are intrinsically tied, as you will explore later.

Some of the theories presented are meant to help you understand how intertwined computer science theories and their applications are, as well as their relevance to what we do each day.

In this section, we learned about theoretical computer science. We also learned about its various theories. Throughout this book, we will be using computational thinking (discussed further in Chapter 2, Elements of Computational Thinking) to help us tackle problems, from the most basic applications to some complex analyses, by defining and designing adequate algorithms that use these theories. Theoretical computer science is used to study a system’s software, which we will explore next.