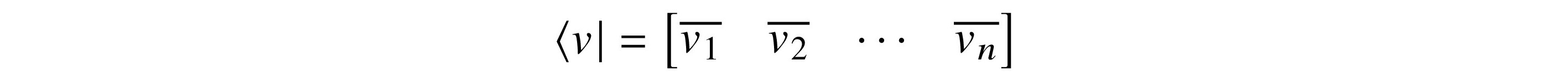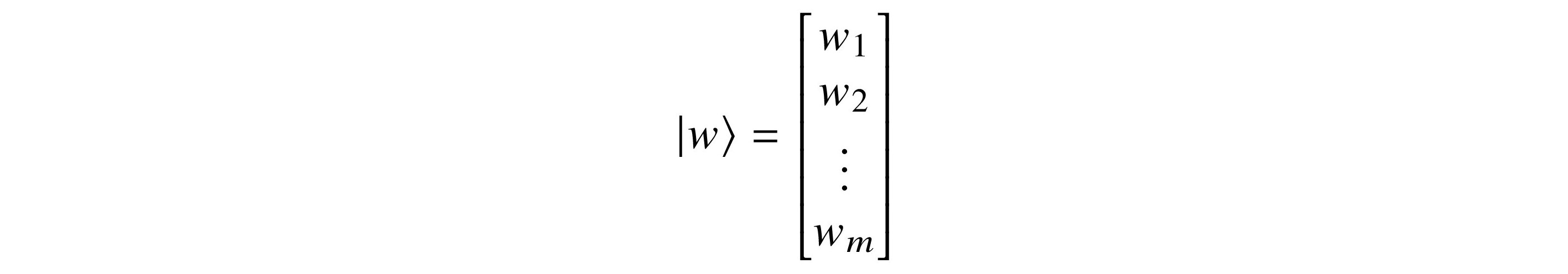One Qubit

Anyone who is not shocked by quantum theory has not understood it.

Niels Bohr
11

A quantum bit, or qubit, is the fundamental information unit of quantum computing. In this chapter, I give a mathematical definition of a qubit based on the foundational material in the first part of this book. Together, we examine the operations you can perform on a single qubit from mathematical and computational perspectives. qubit

Despite a single qubit living in a seemingly strange two-dimensional complex Hilbert space, we can visualize it, its superposition, and its behavior by projecting it onto the surface of a sphere in R³.

All vector spaces considered in this chapter are over C, the field of complex numbers introduced in section 3.9. All bases are orthonormal unless otherwise specified. vector$orthonormal

Topics covered in this chapter

1. 7.1. Introducing quantum bits
2. 7.2. Bras and kets
3. 7.3. The complex math and physics of a single qubit
   1. 7.3.1. Quantum state representation
   2. 7.3.2. Unitary matrices mapping to standard form
   3. 7.3.3. The density matrix
   4. 7.3.4. Observables and expectation
4. 7.4. A nonlinear projection
5. 7.5. The Bloch sphere
6. 7.6. Professor Hadamard, meet Professor Pauli
   1. 7.6.1. The quantum ID gate
   2. 7.6.2. The quantum X gate
   3. 7.6.3. The quantum Z gate
   4. 7.6.4. The quantum Y gate
   5. 7.6.5. The quantum H gate
   6. 7.6.6. The quantum Rφ gates
   7. 7.6.7. The quantum S gate
   8. 7.6.8. The quantum S† gate
   9. 7.6.9. The quantum T gate
   10. 7.6.10. The quantum T† gate
   ...

7.1 Introducing quantum bits

If you have seen descriptions of qubits elsewhere, you may have read something like “a qubit implements a two-state quantum mechanical system and is the quantum analog of a classical bit.” As we saw in section 2.1, a bit also has two states, 0 and 1.

Those other discussions usually include one or more of the following: light switches, spinning electrons, polarized light, and rotating coins or donuts. These approaches have merit and are the basis for teasing apart the difference between the quantum and classical situations. The electron and polarized light examples do depict quantum systems.

Otherwise, analogies tend to be imperfect and eventually may lead you into corners where their behavior and your understanding are not consistent with the actual situation. For this reason, we developed the essential mathematics and insight to reason accurately what happens in quantum computing.

Let’s begin by thinking...

7.2 Bras and kets

It’s now time to formalize our understanding of |0⟩ and |1⟩ and relate them to the discussion of linear algebra in Chapter 5, “Dimensions.”

When we previously looked at vector notation in section 5.4.2, we saw several forms, such as bra ket vector$bra vector$ket Dirac, Paul Dirac bra-ket notation ⟨ | (bra) | ⟩ (ket)

We now add two more invented by Paul Dirac, an English theoretical physicist, for use in quantum mechanics. They simplify many of the expressions we use in quantum computing.

Given a vector v = (v₁, v₂, …, v_n), we denote by ⟨v|, pronounced “bra-v,” the row vector

where we take the complex conjugate of each entry.

For w = (w₁, w₂, …, w_m), |w⟩, pronounced “ket-w,” is the column vector

without the conjugations.

To avoid notational overload, I continue to put vector...

7.3 The complex math and physics of a single qubit

Let’s revisit our definition of a qubit from section 7.1. This time, we break it into two pieces: a mathematical and a physical/quantum mechanical part.

Mathematics

A qubit—a quantum bit—is the fundamental unit of quantum information. At any given time, it is in a superposition state represented by a linear combination of vectors |0⟩ and |1⟩ in C²:

Physics

Through measurement, a qubit is forced to collapse irreversibly to either |0⟩ or |1⟩. The probability of its doing either is |a|² and |b|², respectively. a and b are called probability amplitudes.

When we measure, do we get a bit 0 or 1, or a qubit |0⟩ or |1⟩? Technically, it is the former, but by abuse of notation, we often show it as the latter. You can only get 0 when you measure |0⟩, and you can only get 1 when...

7.4 A nonlinear projection

In Chapter 5, “Dimensions,” we saw linear projections, such as mapping any point in the real plane to the line y = x. Now, we look at a special kind of projection that is nonlinear. We map almost every point on the unit circle onto a line. We will use this in the next section when we discuss the Bloch sphere.

Figure 7.3 shows a unit circle and the line y = –1 that sits right below it.

Figure 7.3: The unit circle in R² resting on the line y = –1

We can map every point on the circle except (0, 1), the north pole, to a point on the line y = –1. We simply draw a line from (0, 1) through the point on the circle. The result is where that line intersects y = –1, as shown in Figure 7.4. The south pole maps to itself. We want different points on the circle to map to different points on the line.

Figure 7.4: Projecting...

7.5 The Bloch sphere

We describe the state of a qubit by a vector Bloch sphere

in C² with r¹ and r² nonnegative numbers in R.

The magnitudes r¹ and r² are related by r₁² + r₂² = 1. This is a mathematical condition.

We saw in section 7.3 that it’s the relative phase of φ₂ – φ₁ that is significant and not the individual phases φ₁ and φ₂. This is a physical condition and means we can take a to be real.

We also saw that we could represent a quantum state as

We do this via a nonlinear projection and a change of coordinates and get a point on the surface of the Bloch sphere, shown in Figure 7.7.

Figure 7.7: The Bloch sphere

The two angles have the ranges 0 ≤ θ ≤ π and 0 ≤ φ < 2π. θ is measured from the positive z-axis and φ from the positive x-axis in the xy-plane.

The nonlinear...

7.6 Professor Hadamard, meet Professor Pauli

Other than mapping the state of a qubit to a Bloch sphere and looking at it differently, what can you do with a qubit? This section looks at the operations, also called gates, which you can apply to a single qubit. Later, we expand our exploration to gates with multiple qubits as inputs and outputs. In Chapter 9, “Wiring Up the Circuits,” we build circuits with these gates to implement algorithms. gate$quantum gate$reversible

Here, for example, is a circuit with one qubit initialized to |0⟩ that performs one operation, X, and then measures the qubit. The result of the measurement is |m₀⟩.

Quantum gates are always reversible, but some other operations are not. Quantum gates correspond to unitary transformations. Measurement is irreversible, and so is the |0⟩ RESET operation described in section 7.6.14. operation$measurement operation$|0⟩ RESET`gate-style |0⟩ RESET...

7.7 Gates and unitary matrices

The collection of all 2-by-2 unitary matrices (section 5.8) with entries in C form a group under multiplication called the unitary group of degree 2. We denote it by U(2, C). It is a subgroup of GL(2, C), the general linear group of degree 2 over C.

Every 1-qubit gate corresponds to such a unitary matrix. We can create all 2-by-2 unitary matrices from the identity and Pauli matrices. Pauli$matrix matrix$Pauli operator$Pauli

We can write any U(2, C) as a product of a complex unit times a linear combination of unitary matrices

with

where we have the following definitions, properties, and identities:

• 0 ≤ θ < 2π
• c_I2 is in R
• c_σx, c_σy, and c_σz are in C
• |c_I2|² + |c_σx|² + |c_σy|² + |c_σz|² = 1

and

The complex unit only affects the global phase of the qubit state and so...

7.8 Summary

The quantum states of a qubit are the unit vectors in C², where we identify two states as equivalent if they differ only by a multiple of a complex unit. To better visualize actions on a qubit, we introduced the Bloch sphere in R³ and showed where special orthonormal bases map onto the sphere.

Any new idea seems to deserve its own notation, and we did not disappoint when we introduced Dirac’s bra-ket representation of vectors. This significantly simplifies calculation when working with multiple qubits.

Given the ket form of qubit states, we introduced the standard 1-qubit gate operations. In the classical case in section 2.4, we could only perform one operation on a single bit, not. In the quantum case, there are many (in fact, an infinite number) of single-qubit operations.

We next look at how to work with two or more qubits and the quantum gates that operate on them. We also introduce entanglement, an essential notion from quantum mechanics...