Graphs and distributions and how to map between them

In this section, we will focus on the mappings between the statistical and graphical properties of a system.

To be more precise, we’ll be interested in understanding how to translate between graphical and statistical independencies. In a perfect world, we’d like to be able to do it in both directions: from graph independence to statistical independence and the other way around.

It turns out that this is possible under certain assumptions.

The key concept in this chapter is one of independence. Let’s start by reviewing what it means.

How to talk about independence

Generally speaking, we say that two variables, and , are independent when our knowledge about does not change our knowledge about (and vice versa). In terms of probability distributions, we can express it in the following way:

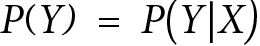
In other words: the marginal probability of is the same as the conditional probability of given...

Chains, forks, and colliders or…immoralities

On a sunny morning of June 1, 2020, Mr. Huang was driving his gleaming white Tesla on one of Taiwan’s main highways. The day was clear, and the trip was going smoothly. Mr. Huang engaged the autopilot and set the speed to 110 km/h. While approaching the road’s 268-kilometer mark, he was completely unaware that only 300 meters ahead, something unexpected was awaiting him. Nine minutes earlier, another driver, Mr. Yeh, had lost control of his vehicle. His white truck was now overturned, almost fully blocking two lanes of the highway right at the 268.3-kilometer mark.

Around 11 seconds later, to Mr. Huang’s dismay, his Tesla crashed into the overturned truck’s rooftop. Fortunately, the driver, Mr. Huang, survived the crash and came out of the accident without any serious injuries (Everington, 2020).

A chain of events

Many modern cars are equipped with some sort of collision warning or collision prevention...

Forks, chains, colliders, and regression

In this section, we will see how the properties of chains, forks, and colliders manifest themselves in regression analysis. The very type of analysis that we’ll conduct in this section is actually at the heart of some of the most classic methods of causal inference and causal discovery that we’ll be working with in the next two parts of this book.

What we’re going to do now is to generate three datasets, each with three variables, , , and . Each dataset will be based on a graph representing one of the three structures: a chain, a fork, or a collider. Next, we’ll fit one regression model per dataset, regressing on the remaining two variables, and analyze the results. On the way, we’ll plot pairwise scatterplots for each dataset to strengthen our intuitive understanding of a link between graphical structures, statistical models, and visual data representations.

Let’s start with graphs. Figure 5...

Wrapping it up

This chapter introduced us to the three basic conditional independence structures – chains, forks, and colliders (the latter also known as immoralities or v-structures). We studied the properties of these structures and demonstrated that colliders have unique properties that make constraint-based causal discovery possible. We discussed how to deal with cases when it’s impossible to orient all the edges in a graph and introduced the concept of MECs. Finally, we got our hands dirty with coding the examples of all the structures and analyzed their statistical properties using multiple linear regression.

This chapter concludes the first, introductory part of this book. The next chapter starts on the other side, in the fascinating land of causal inference. We’ll go beyond simple linear cases and see a whole new zoo of models.

Ready?

References

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.

Everington, K. (2020, Jun 2). Video shows Tesla on autopilot slam into truck on Taiwan highway. Taiwan News. https://www.taiwannews.com.tw/en/news/3943199.

Lauritzen, S. L. (1996). Graphical Models. Oxford University Press.

Neal, B. (2020, December, 17). Introduction to Causal Inference from a Machine Learning Perspective [Lecture notes]. https://www.bradyneal.com/Introduction_to_Causal_Inference-Dec17_2020-Neal.pdf.

Pearl, J. (2009). Causality. Cambridge, UK: Cambridge University Press.

Peters, J., Janzing, D. & Schölkopf, B. (2017). Elements of Causal Inference: Foundations and Learning Algorithms. MIT Press.

Pearl, J., & Mackenzie, D. (2019). The Book of Why. Penguin Books.

Scheines, R. (1996). An introduction to causal inference. [Manuscript]

Spirtes, P., Glymour, C., & Scheines, R. (2000). Causation, Prediction, and Search. MIT Press.

Uhler, C., Raskutti...

References

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.

Everington, K. (2020, Jun 2). Video shows Tesla on autopilot slam into truck on Taiwan highway. Taiwan News. https://www.taiwannews.com.tw/en/news/3943199.

Lauritzen, S. L. (1996). Graphical Models. Oxford University Press.

Neal, B. (2020, December, 17). Introduction to Causal Inference from a Machine Learning Perspective [Lecture notes]. https://www.bradyneal.com/Introduction_to_Causal_Inference-Dec17_2020-Neal.pdf.

Pearl, J. (2009). Causality. Cambridge, UK: Cambridge University Press.

Peters, J., Janzing, D. & Schölkopf, B. (2017). Elements of Causal Inference: Foundations and Learning Algorithms. MIT Press.

Pearl, J., & Mackenzie, D. (2019). The Book of Why. Penguin Books.

Scheines, R. (1996). An introduction to causal inference. [Manuscript]

Spirtes, P., Glymour, C., & Scheines, R. (2000). Causation, Prediction, and Search. MIT Press.

Uhler, C., Raskutti...

Join our book's Discord space

Join our Discord community to meet like-minded people and learn alongside more than 2000 members at: https://packt.link/infer