Throughout this book, we have learned about various types of neural networks that are used in deep learning, such as convolutional neural networks and recurrent neural networks, and they have achieved some tremendous results in a variety of tasks, such as computer vision, image reconstruction, synthetic data generation, speech recognition, language translation, and so on. All of the models we have looked at so far have been trained on Euclidean data, that is, data that can be represented in grid (matrix) format—images, text, audio, and so on.
However, many of the tasks that we would like to apply deep learning to use non-Euclidean data (more on this shortly) – the kind that the neural networks we have come across so far are unable to process and deal with. This includes dealing with sensor networks, mesh surfaces, point clouds, objects (the...

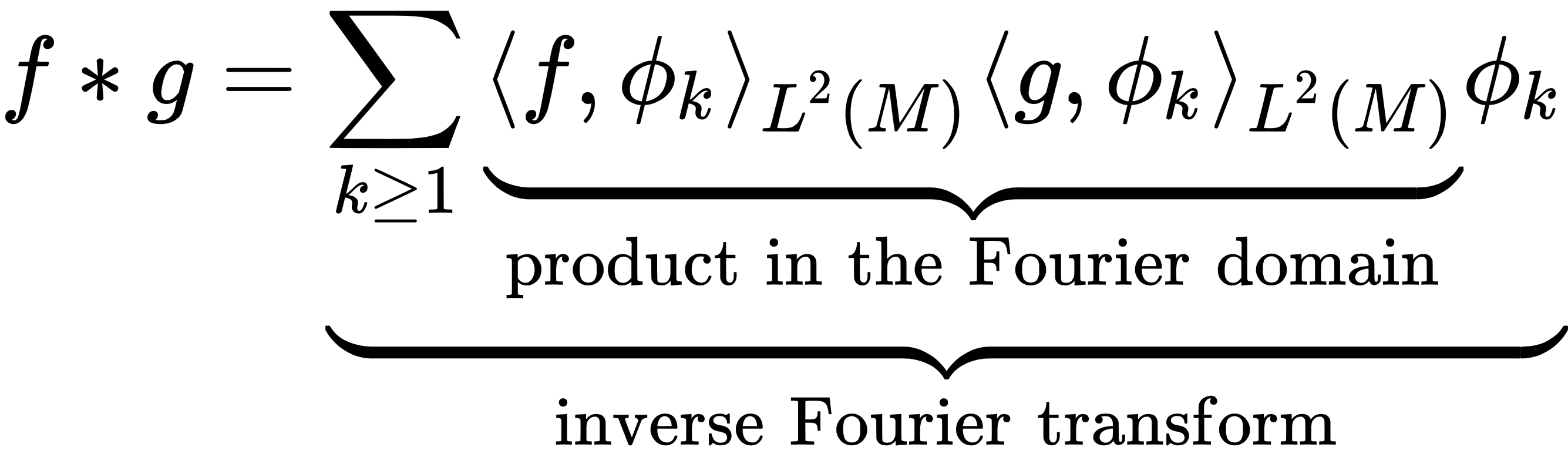
 . We can rewrite this in matrix form as follows:
. We can rewrite this in matrix form as follows: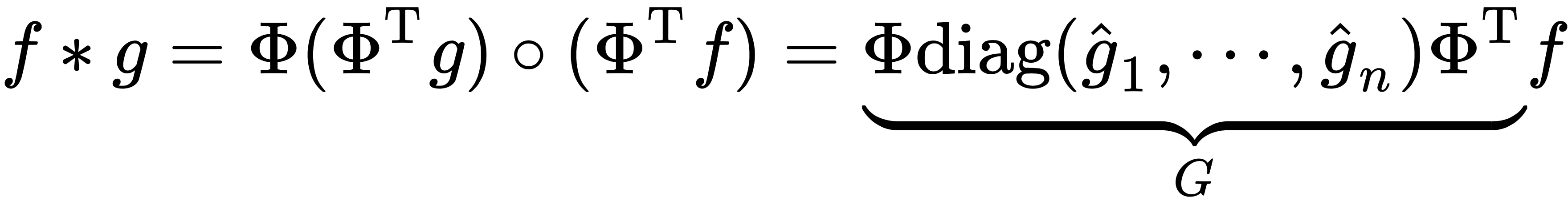
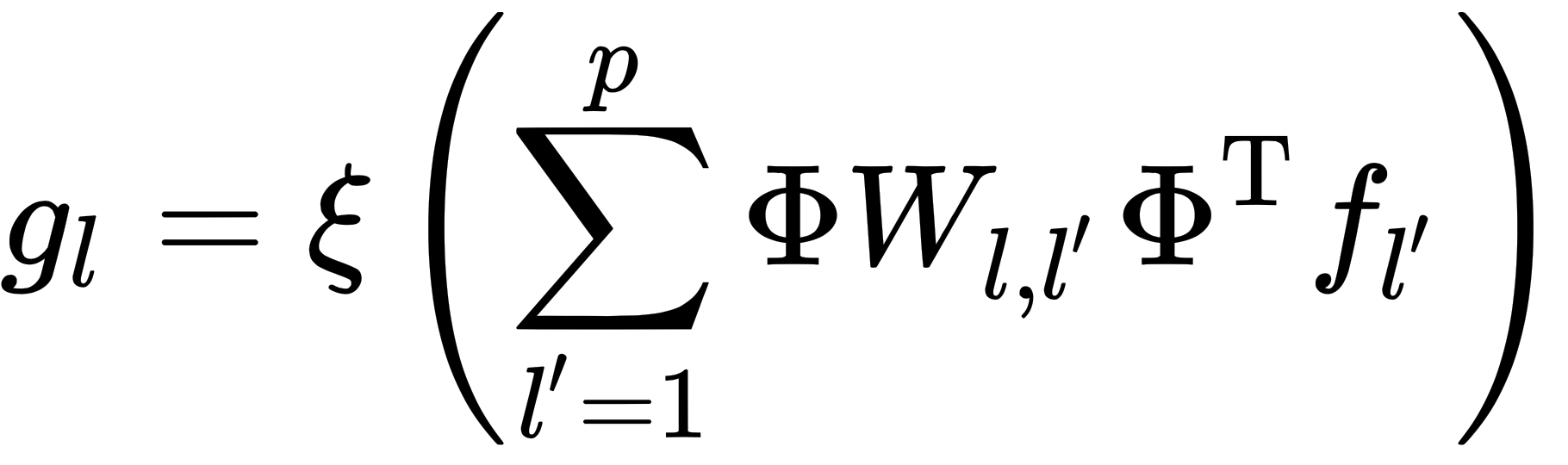
 ,
,  , and
, and  is an n×n diagonal matrix of spectral filter coefficients (which are basis-dependent, meaning that they don't generalize over different graphs and are limited to a single domain), and ξ is the nonlinearity that's applied to the vertex-wise function values.
is an n×n diagonal matrix of spectral filter coefficients (which are basis-dependent, meaning that they don't generalize over different graphs and are limited to a single domain), and ξ is the nonlinearity that's applied to the vertex-wise function values.  , around x. This is referred to as a geodesic polar. On each of these coordinates, we apply a set of parametric kernels,
, around x. This is referred to as a geodesic polar. On each of these coordinates, we apply a set of parametric kernels,  , that produces local weights.
, that produces local weights. 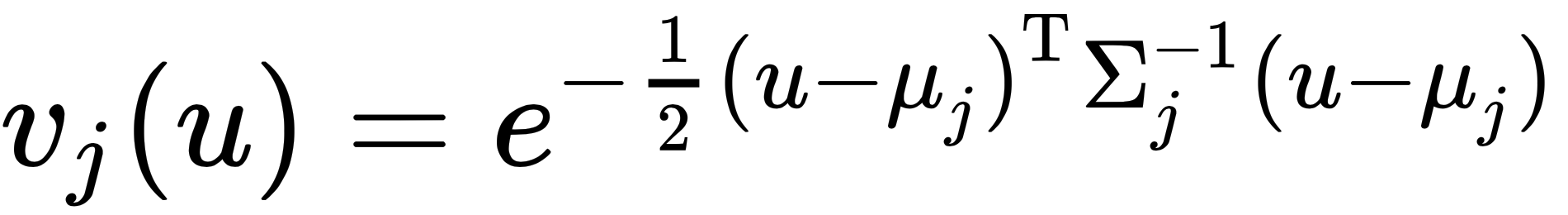
 and
and  ) are trainable and learned.
) are trainable and learned. 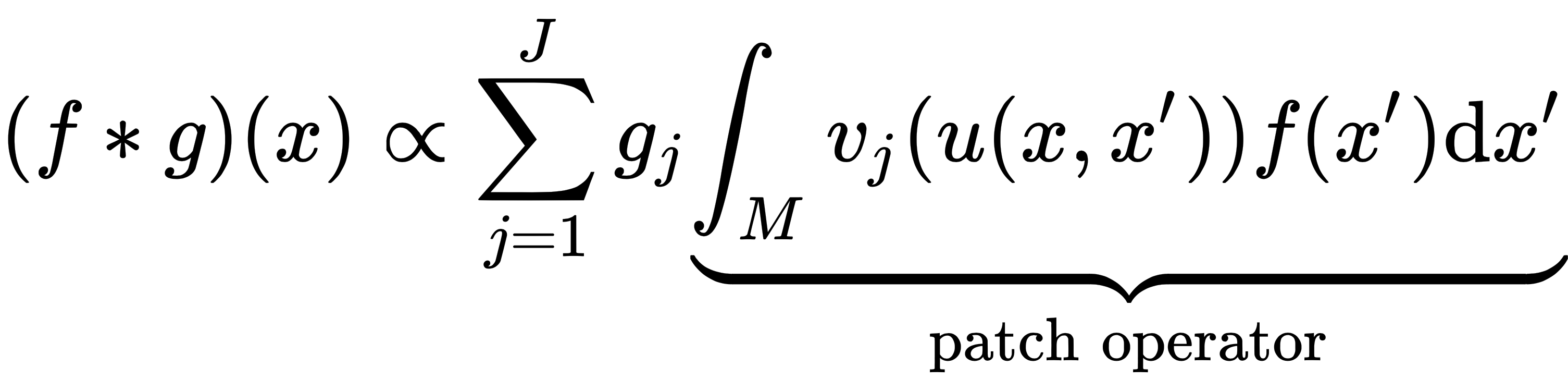
 is a feature at vertex i.
is a feature at vertex i.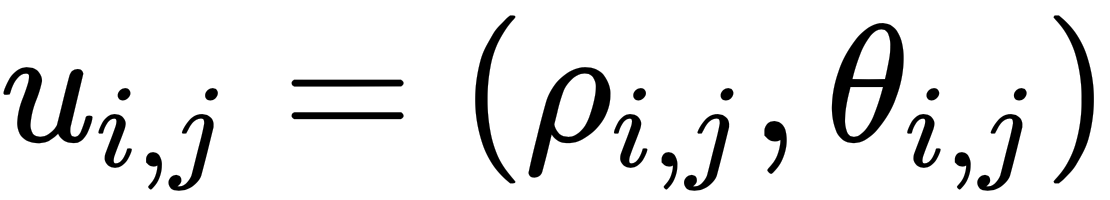
 is the geodesic distance between i and j and
is the geodesic distance between i and j and  is the...
is the... contains the d-dimensional pseudo-coordinates,
contains the d-dimensional pseudo-coordinates,  , where
, where  . The node feature matrix is denoted as
. The node feature matrix is denoted as  , where each of the nodes contains d-dimensional features. We then define the lth channel of the feature map as fl, of which the ith node...
, where each of the nodes contains d-dimensional features. We then define the lth channel of the feature map as fl, of which the ith node...