Vector Calculus

Most of you will likely have had some exposure to calculus in the past, be it in high school, college, or university, and were likely hoping to never have to deal with it again. However, calculus is not only one of the most profound discoveries in mathematics; it also plays a vital role in deep learning.

In this chapter, we will start by introducing core concepts of calculus using single variable calculus, and then we will move on to multivariable calculus and extend everything we learned in multivariable calculus to gain an understanding of vector calculus and its relation to deep learning.

This chapter will cover the following topics:

• Single variable calculus
• Multivariable calculus
• Vector calculus

Single variable calculus

At its core, calculus is nothing more than the study of relationships and change. Having a keen grasp of calculus will help you better understand how deep learning algorithms work and how to make them work better for you as a practitioner.

Let's move on to understanding what makes calculus such a powerful tool. We start with single variable calculus, which is about functions that take in a single input and produce a single output.

Derivatives

To start with, let's imagine a straight line with the following equation:

In the equation, the following aspects apply:

• y is a function of x, often written simply as f(x) (which is the notation we will be predominantly using in the remainder of the...

Multivariable calculus

Now that we have gone through single variable calculus and understand what calculus is about, it is time for us to go a step deeper and look at multivariable calculus. Multivariable calculus has a lot of similarities with single variable calculus, except—as the name suggests—here, we will be dealing with functions that accept two or more variables as input.

Multivariable calculus is used everywhere in the real world and has applications in every field and industry, from healthcare to economics, to finance, to robotics, to aerospace, and so on. An example of this could be trying to model how air curves around an airplane, to understand how aerodynamic it is and where the design of the airplane body can be improved. This is something we would not be able to do with single variable calculus.

...

Vector calculus

When we find derivatives of functions with respect to vectors, we need to be a lot more diligent. And as we will see in Chapter 2, Linear Algebra, vectors and matrices are noncommutative and behave quite differently from scalars, and so we need to find a different way to differentiate them.

Derivatives

Earlier, we saw that functions are differentiated by using the limit of the variable in the quotient. But vectors, as we know, are not like scalars in that we cannot divide by vectors, which creates the need for new definitions for vector-valued functions.

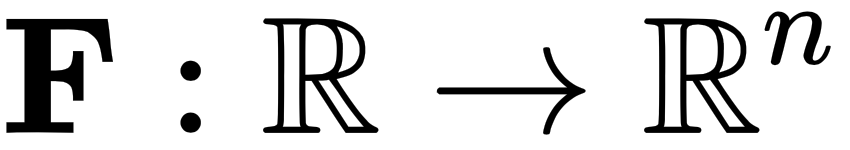We can define a vector function as a function —that is, it takes in a scalar value as input and outputs a vector. So, the derivative of F is defined...

Summary

And with that, we conclude our chapter on calculus. So far, we have learned about the fundamental concepts of single variable, multivariable, and vector calculus, and what it is that makes them so useful.

In the next chapter, we will move on to probability and statistics, and see how what we learned in linear algebra and calculus carries over into these fields.