Gradient for functions with respect to a real-valued matrix A is defined as the matrix of partial derivatives of A and is denoted as follows:
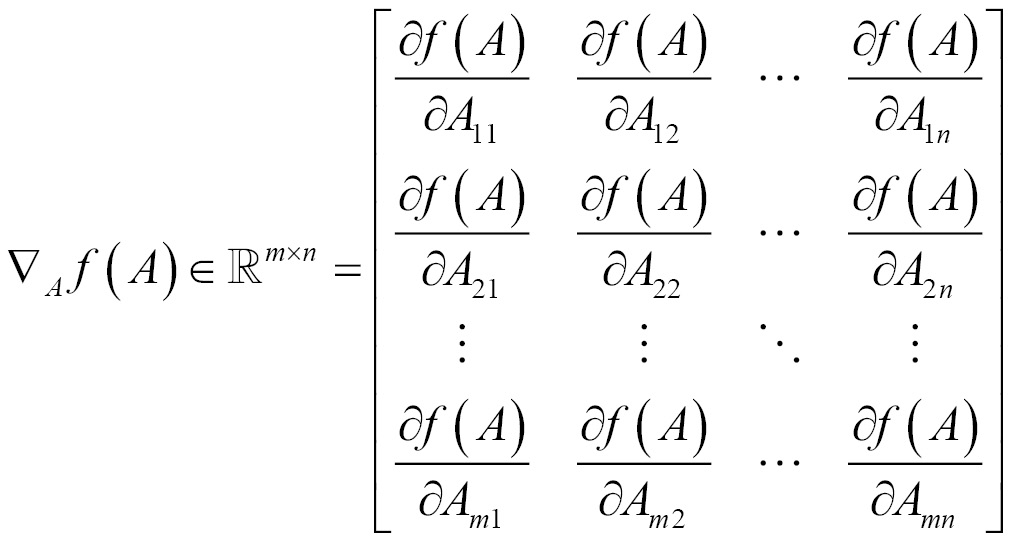
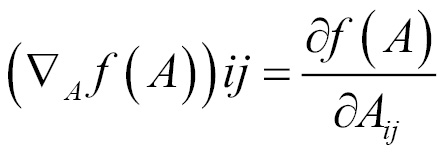
TensorFlow does not do numerical differentiation; rather, it supports automatic differentiation. By specifying operations in a TensorFlow graph, it can automatically run the chain rule through the graph and, as it knows the derivatives of each operation we specify, it can combine them automatically.
The following example shows training a network using MNIST data, the MNIST database consists of handwritten digits. It has a training set of 60,000 examples and a test set of 10,000 samples. The digits are size-normalized.
Here backpropagation is performed without any API usage and derivatives are calculated manually. We get 913 correct out of 1,000 tests. This concept will be introduced in the next chapter.
The following code snippet describes how to get the mnist dataset and initialize weights and biases:
import tensorflow as tf
# get mnist dataset
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets("MNIST_data/", one_hot=True)
# x represents image with 784 values as columns (28*28), y represents output digit
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])
# initialize weights and biases [w1,b1][w2,b2]
numNeuronsInDeepLayer = 30
w1 = tf.Variable(tf.truncated_normal([784, numNeuronsInDeepLayer]))
b1 = tf.Variable(tf.truncated_normal([1, numNeuronsInDeepLayer]))
w2 = tf.Variable(tf.truncated_normal([numNeuronsInDeepLayer, 10]))
b2 = tf.Variable(tf.truncated_normal([1, 10]))
We now define a two-layered network with a nonlinear sigmoid function; a squared loss function is applied and optimized using a backward propagation algorithm, as shown in the following snippet:
# non-linear sigmoid function at each neuron
def sigmoid(x):
sigma = tf.div(tf.constant(1.0), tf.add(tf.constant(1.0), tf.exp(tf.negative(x))))
return sigma
# starting from first layer with wx+b, then apply sigmoid to add non-linearity
z1 = tf.add(tf.matmul(x, w1), b1)
a1 = sigmoid(z1)
z2 = tf.add(tf.matmul(a1, w2), b2)
a2 = sigmoid(z2)
# calculate the loss (delta)
loss = tf.subtract(a2, y)
# derivative of the sigmoid function der(sigmoid)=sigmoid*(1-sigmoid)
def sigmaprime(x):
return tf.multiply(sigmoid(x), tf.subtract(tf.constant(1.0), sigmoid(x)))
# backward propagation
dz2 = tf.multiply(loss, sigmaprime(z2))
db2 = dz2
dw2 = tf.matmul(tf.transpose(a1), dz2)
da1 = tf.matmul(dz2, tf.transpose(w2))
dz1 = tf.multiply(da1, sigmaprime(z1))
db1 = dz1
dw1 = tf.matmul(tf.transpose(x), dz1)
# finally update the network
eta = tf.constant(0.5)
step = [
tf.assign(w1,
tf.subtract(w1, tf.multiply(eta, dw1)))
, tf.assign(b1,
tf.subtract(b1, tf.multiply(eta,
tf.reduce_mean(db1, axis=[0]))))
, tf.assign(w2,
tf.subtract(w2, tf.multiply(eta, dw2)))
, tf.assign(b2,
tf.subtract(b2, tf.multiply(eta,
tf.reduce_mean(db2, axis=[0]))))
]
acct_mat = tf.equal(tf.argmax(a2, 1), tf.argmax(y, 1))
acct_res = tf.reduce_sum(tf.cast(acct_mat, tf.float32))
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
for i in range(10000):
batch_xs, batch_ys = data.train.next_batch(10)
sess.run(step, feed_dict={x: batch_xs,
y: batch_ys})
if i % 1000 == 0:
res = sess.run(acct_res, feed_dict=
{x: data.test.images[:1000],
y: data.test.labels[:1000]})
print(res)
The output of this is shown as follows:
Extracting MNIST_data
125.0
814.0
870.0
874.0
889.0
897.0
906.0
903.0
922.0
913.0
Now, let's use automatic differentiation with TensorFlow. The following example demonstrates the use of GradientDescentOptimizer. We get 924 correct out of 1,000 tests.
import tensorflow as tf
# get mnist dataset
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets("MNIST_data/", one_hot=True)
# x represents image with 784 values as columns (28*28), y represents output digit
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])
# initialize weights and biases [w1,b1][w2,b2]
numNeuronsInDeepLayer = 30
w1 = tf.Variable(tf.truncated_normal([784, numNeuronsInDeepLayer]))
b1 = tf.Variable(tf.truncated_normal([1, numNeuronsInDeepLayer]))
w2 = tf.Variable(tf.truncated_normal([numNeuronsInDeepLayer, 10]))
b2 = tf.Variable(tf.truncated_normal([1, 10]))
# non-linear sigmoid function at each neuron
def sigmoid(x):
sigma = tf.div(tf.constant(1.0), tf.add(tf.constant(1.0), tf.exp(tf.negative(x))))
return sigma
# starting from first layer with wx+b, then apply sigmoid to add non-linearity
z1 = tf.add(tf.matmul(x, w1), b1)
a1 = sigmoid(z1)
z2 = tf.add(tf.matmul(a1, w2), b2)
a2 = sigmoid(z2)
# calculate the loss (delta)
loss = tf.subtract(a2, y)
# derivative of the sigmoid function der(sigmoid)=sigmoid*(1-sigmoid)
def sigmaprime(x):
return tf.multiply(sigmoid(x), tf.subtract(tf.constant(1.0), sigmoid(x)))
# automatic differentiation
cost = tf.multiply(loss, loss)
step = tf.train.GradientDescentOptimizer(0.1).minimize(cost)
acct_mat = tf.equal(tf.argmax(a2, 1), tf.argmax(y, 1))
acct_res = tf.reduce_sum(tf.cast(acct_mat, tf.float32))
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
for i in range(10000):
batch_xs, batch_ys = data.train.next_batch(10)
sess.run(step, feed_dict={x: batch_xs,
y: batch_ys})
if i % 1000 == 0:
res = sess.run(acct_res, feed_dict=
{x: data.test.images[:1000],
y: data.test.labels[:1000]})
print(res)
The output of this is shown as follows:
96.0
777.0
862.0
870.0
889.0
901.0
911.0
905.0
914.0
924.0
The following example shows linear regression using gradient descent:
import tensorflow as tf
import numpy
import matplotlib.pyplot as plt
rndm = numpy.random
# config parameters
learningRate = 0.01
trainingEpochs = 1000
displayStep = 50
# create the training data
trainX = numpy.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,
7.042,10.791,5.313,7.997,5.654,9.27,3.12])
trainY = numpy.asarray([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,
2.827,3.465,1.65,2.904,2.42,2.94,1.34])
nSamples = trainX.shape[0]
# tf inputs
X = tf.placeholder("float")
Y = tf.placeholder("float")
# initialize weights and bias
W = tf.Variable(rndm.randn(), name="weight")
b = tf.Variable(rndm.randn(), name="bias")
# linear model
linearModel = tf.add(tf.multiply(X, W), b)
# mean squared error
loss = tf.reduce_sum(tf.pow(linearModel-Y, 2))/(2*nSamples)
# Gradient descent
opt = tf.train.GradientDescentOptimizer(learningRate).minimize(loss)
# initializing variables
init = tf.global_variables_initializer()
# run
with tf.Session() as sess:
sess.run(init)
# fitting the training data
for epoch in range(trainingEpochs):
for (x, y) in zip(trainX, trainY):
sess.run(opt, feed_dict={X: x, Y: y})
# print logs
if (epoch+1) % displayStep == 0:
c = sess.run(loss, feed_dict={X: trainX, Y:trainY})
print("Epoch is:", '%04d' % (epoch+1), "loss=", "{:.9f}".format(c), "W=", sess.run(W), "b=", sess.run(b))
print("optimization done...")
trainingLoss = sess.run(loss, feed_dict={X: trainX, Y: trainY})
print("Training loss=", trainingLoss, "W=", sess.run(W), "b=", sess.run(b), '\n')
# display the plot
plt.plot(trainX, trainY, 'ro', label='Original data')
plt.plot(trainX, sess.run(W) * trainX + sess.run(b), label='Fitted line')
plt.legend()
plt.show()
# Testing example, as requested (Issue #2)
testX = numpy.asarray([6.83, 4.668, 8.9, 7.91, 5.7, 8.7, 3.1, 2.1])
testY = numpy.asarray([1.84, 2.273, 3.2, 2.831, 2.92, 3.24, 1.35, 1.03])
print("Testing... (Mean square loss Comparison)")
testing_cost = sess.run(
tf.reduce_sum(tf.pow(linearModel - Y, 2)) / (2 * testX.shape[0]),
feed_dict={X: testX, Y: testY})
print("Testing cost=", testing_cost)
print("Absolute mean square loss difference:", abs(trainingLoss - testing_cost))
plt.plot(testX, testY, 'bo', label='Testing data')
plt.plot(trainX, sess.run(W) * trainX + sess.run(b), label='Fitted line')
plt.legend()
plt.show()
The output of this is shown as follows:
Epoch is: 0050 loss= 0.141912043 W= 0.10565 b= 1.8382
Epoch is: 0100 loss= 0.134377643 W= 0.11413 b= 1.7772
Epoch is: 0150 loss= 0.127711013 W= 0.122106 b= 1.71982
Epoch is: 0200 loss= 0.121811897 W= 0.129609 b= 1.66585
Epoch is: 0250 loss= 0.116592340 W= 0.136666 b= 1.61508
Epoch is: 0300 loss= 0.111973859 W= 0.143304 b= 1.56733
Epoch is: 0350 loss= 0.107887231 W= 0.149547 b= 1.52241
Epoch is: 0400 loss= 0.104270980 W= 0.15542 b= 1.48017
Epoch is: 0450 loss= 0.101070963 W= 0.160945 b= 1.44043
Epoch is: 0500 loss= 0.098239250 W= 0.166141 b= 1.40305
Epoch is: 0550 loss= 0.095733419 W= 0.171029 b= 1.36789
Epoch is: 0600 loss= 0.093516059 W= 0.175626 b= 1.33481
Epoch is: 0650 loss= 0.091553882 W= 0.179951 b= 1.3037
Epoch is: 0700 loss= 0.089817807 W= 0.184018 b= 1.27445
Epoch is: 0750 loss= 0.088281371 W= 0.187843 b= 1.24692
Epoch is: 0800 loss= 0.086921677 W= 0.191442 b= 1.22104
Epoch is: 0850 loss= 0.085718453 W= 0.194827 b= 1.19669
Epoch is: 0900 loss= 0.084653646 W= 0.198011 b= 1.17378
Epoch is: 0950 loss= 0.083711281 W= 0.201005 b= 1.15224
Epoch is: 1000 loss= 0.082877308 W= 0.203822 b= 1.13198
optimization done...
Training loss= 0.0828773 W= 0.203822 b= 1.13198
Testing... (Mean square loss Comparison)
Testing cost= 0.0957726
Absolute mean square loss difference: 0.0128952
The plots are as follows:
The following image shows the fitted line on testing data using the model:
 United States
United States
 Great Britain
Great Britain
 India
India
 Germany
Germany
 France
France
 Canada
Canada
 Russia
Russia
 Spain
Spain
 Brazil
Brazil
 Australia
Australia
 Singapore
Singapore
 Canary Islands
Canary Islands
 Hungary
Hungary
 Ukraine
Ukraine
 Luxembourg
Luxembourg
 Estonia
Estonia
 Lithuania
Lithuania
 South Korea
South Korea
 Turkey
Turkey
 Switzerland
Switzerland
 Colombia
Colombia
 Taiwan
Taiwan
 Chile
Chile
 Norway
Norway
 Ecuador
Ecuador
 Indonesia
Indonesia
 New Zealand
New Zealand
 Cyprus
Cyprus
 Denmark
Denmark
 Finland
Finland
 Poland
Poland
 Malta
Malta
 Czechia
Czechia
 Austria
Austria
 Sweden
Sweden
 Italy
Italy
 Egypt
Egypt
 Belgium
Belgium
 Portugal
Portugal
 Slovenia
Slovenia
 Ireland
Ireland
 Romania
Romania
 Greece
Greece
 Argentina
Argentina
 Netherlands
Netherlands
 Bulgaria
Bulgaria
 Latvia
Latvia
 South Africa
South Africa
 Malaysia
Malaysia
 Japan
Japan
 Slovakia
Slovakia
 Philippines
Philippines
 Mexico
Mexico
 Thailand
Thailand

















