Chapter 2

(2.1)

(a)It is not a qubit state because it is not normalized (1 ²+1 ² = 2≠1).

(b)It is a qubit state because 4∕7 + 3∕7 = 1.

(c)It is not a qubit state because 2 ²≠1.

(d)It is a qubit state as 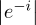² = 1.

(e)We could take x = = 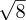∕3.

(f)The values x = (1∕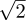)e^i𝜃 for any real 𝜃.

(2.2)

(a)The probability of obtaining 0 will be 1∕2, and so will the that of obtaining 1.

(b)The measurement will always return 0.

(c)The probability of obtaining 0 is 1∕3. That of obtaining 1 is 2∕3.

(d)The probability of obtaining 0 is p. That of obtaining 1 is 1 − p.

(2.3)

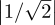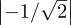All the probabilities are equal to 1∕2 because ² = 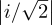² = ² = 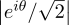² = 1∕2.

(2.4)

The conjugate transpose of U₁ is U₁ itself and a simple verification reveals that U₁^†U₁ = U₁U₁^† = U₁U₁ is equal to the identity matrix. Regarding the other matrices, we have

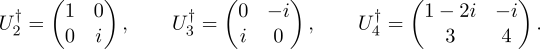
The matrices U₂ and U₃ are unitary, but U₄ is not because

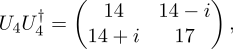
which is not equal...