Chapter 5

1. (5.1)

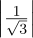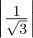(a)It’s valid, because ² + ² + 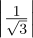² = 1∕3+1∕3+1∕3 = 1.

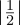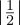(b)It’s valid, because ² + 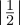² + ² + 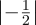² = 1∕4 + 1∕4 + 1∕4 + 1∕4 = 1.

(c)It’s valid, because 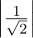² + 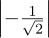² = 1∕2 + 1∕2 = 1.

(d)It’s valid, because 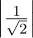² + 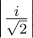² = 1∕2 + 1∕2 = 1.

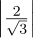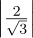(e)It’s not valid, because ² + ² + 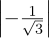² = 4∕3 + 4∕3 + 1∕3 = 9∕3≠1.

(f)It’s valid, because 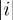² = 1.

(g)It’s not valid, because ² + 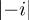² = 5≠1.

(h)It’s valid, because 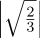² + 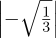² = 2∕3 + 1∕3 = 1.

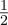
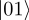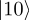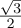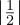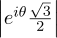The values of x that would make + x a valid state are those of the form e^i𝜃, where 𝜃 is any real number, because ² 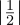+ ² = ² + 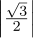² = 1∕4 + 3∕4 = 1.

(5.2)

It is easy to see that

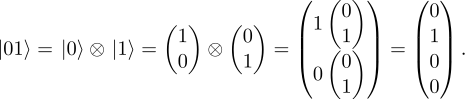
Also, we have that

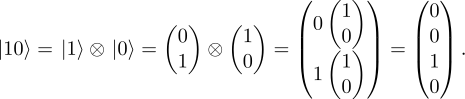
Finally, it holds that

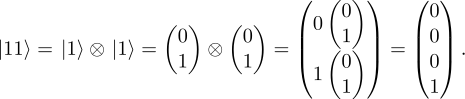
(5.3)

Denote

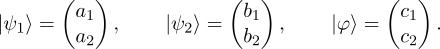
Then it holds that

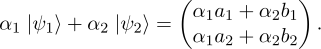
From this, it follows that

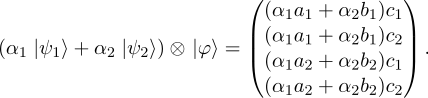
We also know that

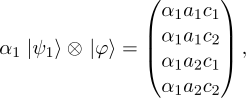
and that

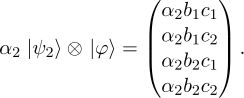
Adding these two vectors together gives us the...