Chapter 10
(10.1)
We would only have to run the following piece of code:
circuit = QuantumCircuit (6)
circuit . mcx ([0,2,4,5], 3)(10.2)
If we wanted to have certainty that the final state is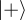 
, it would suffice for us to add a Hadamard gate right before the measurement. By doing this, since unitary matrices are invertible, 
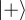(and only 
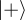) would become 
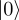)—and all other states would have a non-zero amplitude for 
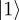. Therefore, if we run a sufficiently large amount of shots and we always get 0 as an outcome, we can be very certain that the state is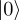 
. Of course, the more shots we run, the more certain we will be!
(10.3)
We can run the following instructions:
state_1 = QuantumCircuit(1)
state_1.x(0)
result_1 = quantum_teleportation(state_1)
print(result_1.get_counts())
We will get that all the outcomes are 1.
(10.4)
The following would be one possible alternative:
oracle = build _ oracle (["010", "111", "011", "100"])
df...
