R Data Analysis Projects

Recommender systems or recommendation engines are a popular class of machine learning algorithms widely used today by online retail companies. With historical data about users and product interactions, a recommender system can make profitable/useful recommendations about users and their product preferences.

In the last decade, recommender systems have achieved great success with both online retailers and brick and mortar stores. They have allowed retailers to move away from group campaigns, where a group of people receive a single offer. Recommender systems technology has revolutionized marketing campaigns. Today, retailers offer a customized recommendation to each of their customers. Such recommendations can dramatically increase customer stickiness.

Retailers design and run sales campaigns to promote up-selling and cross-selling. Up-selling is a technique by which retailers try to push high-value products to their customers. Cross-selling is the practice of selling additional products to customers. Recommender systems provide an empirical method to generate recommendations for retailers up-selling and cross-selling campaigns.

Retailers can now make quantitative decisions based on solid statistics and math to improve their businesses. There are a growing number of conferences and journals dedicated to recommender systems technology, which plays a vital role today at top successful companies such as Amazon.com, YouTube, Netflix, LinkedIn, Facebook, TripAdvisor, and IMDb.

Based on the type and volume of available data, recommender systems of varying complexity and increased accuracy can be built. In the previous paragraph, we defined historical data as a user and his product interactions. Let's use this definition to illustrate the different types of data in the context of recommender systems.

Transactions

Transactions are purchases made by a customer on a single visit to a retail store. Typically, transaction data can include the products purchased, quantity purchased, the price, discount if applied, and a timestamp. A single transaction can include multiple products. It may register information about the user who made the transaction in some cases, where the customer allows the retailer to store his information by joining a rewards program.

A simplified view of the transaction data is a binary matrix. The rows of this matrix correspond to a unique identifier for a transaction; let's call it transaction ID. The columns correspond to the unique identifier for a product; let's call it product ID. The cell values are zero or one, if that product is either excluded or included in the transaction.

A binary matrix with n transactions and m products is given as follows:

Txn/Product	P1	P2	P3	....	Pm
T1	0	1	1	...	0
T2	1	1	1	....	1
...	...	...	...	...	...
Tn	o	1	1	...	1

Weighted transactions

This is additional information added to the transaction to denote its importance, such as the profitability of the transaction as a whole or the profitability of the individual products in the transaction. In the case of the preceding binary matrix, a column called weight is added to store the importance of the transaction.

In this chapter, we will show you how to use transaction data to support cross-selling campaigns. We will see how the derived user product preferences, or recommendations from the user's product interactions (transactions/weighted transactions), can fuel successful cross-selling campaigns. We will implement and understand the algorithms that can leverage this data in R. We will work on a superficial use case in which we need to generate recommendations to support a cross-selling campaign for an imaginative retailer.

Our web application

 

Our goal, by the the end of this chapter, is to understand the concepts of association rule mining and related topics, and solve the given cross-selling campaign problem using association rule mining. We will understand how different aspects of the cross-selling campaign problem can be solved using the family of association rule mining algorithms, how to implement them in R, and finally build the web application to display our analysis and results.

We will be following a code-first approach in this book. The style followed throughout this book is to introduce a real-world problem, following which we will briefly introduce the algorithm/technique that can be used to solve this problem. We will keep the algorithm description brief. We will proceed to introduce the R package that implements the algorithm and subsequently start writing the R code to prepare the data in a way that the algorithm expects. As we invoke the actual algorithm in R and explore the results, we will get into the nitty-gritty of the algorithm. Finally, we will provide further references for curious readers.

A retailer has approached us with a problem. In the coming months, he wants to boost his sales. He is planning a marketing campaign on a large scale to promote sales. One aspect of his campaign is the cross-selling strategy. Cross-selling is the practice of selling additional products to customers. In order to do that, he wants to know what items/products tend to go together. Equipped with this information, he can now design his cross-selling strategy. He expects us to provide him with a recommendation of top N product associations so that he can pick and choose among them for inclusion in his campaign.

He has provided us with his historical transaction data. The data includes his past transactions, where each transaction is uniquely identified by an order_id integer, and the list of products present in the transaction called product_id. Remember the binary matrix representation of transactions we described in the introduction section? The dataset provided by our retailer is in exactly the same format.

Let's start by reading the data provided by the retailer. The code for this chapter was written in RStudio Version 0.99.491. It uses R version 3.3.1. As we work through our example, we will introduce the arules R package that we will be using. In our description, we will be using the terms order/transaction, user/customer, and item/product interchangeably. We will not be describing the installation of R packages used through the code. It's assumed that the reader is well aware of the method for installing an R package and has installed those packages before using it.

This data can be downloaded from:

data.path = '../../data/data.csv'
 data = read.csv(data.path)
 head(data)
order_id product_id
 1 837080 Unsweetened Almondmilk
 2 837080 Fat Free Milk dairy
 3 837080 Turkey
 4 837080 Caramel Corn Rice Cakes
 5 837080 Guacamole Singles
 6 837080 HUMMUS 10OZ WHITE BEAN EAT WELL

The given data is in a tabular format. Every row is a tuple of order_id, representing the transaction, product_id, the item included in that transaction, and the department_id, that is the department to which the item belongs to. This is our binary data representation, which is absolutely tenable for the classical association rule mining algorithm. This algorithm is also called market basket analysis, as we are analyzing the customer's basket—the transactions. Given a large database of customer transactions where each transaction consists of items purchased by a customer during a visit, the association rule mining algorithm generates all significant association rules between the items in the database.

Let's quickly explore our data. We can count the number of unique transactions and the number of unique products:

library(dplyr)
data %>%
 group_by('order_id') %>%
 summarize(order.count = n_distinct(order_id))

 data %>%
 group_by('product_id') %>%
 summarize(product.count = n_distinct(product_id))
# A tibble: 1 <U+00D7> 2
 `"order_id"` order.count
 <chr> <int>
 1 order_id 6988
# A tibble: 1 <U+00D7> 2
 `"product_id"` product.count
 <chr> <int>
 1 product_id 16793

We have 6988 transactions and 16793 individual products. There is no information about the quantity of products purchased in a transaction. We have used the dplyr library to perform these aggregate calculations, which is a library used to perform efficient data wrangling on data frames.

In the next section, we will introduce the association rule mining algorithm. We will explain how this method can be leveraged to generate the top N product recommendations requested by the retailer for his cross-selling campaign.

There are several algorithmic implementations for association rule mining. Key among them is the apriori algorithm by Rakesh Agrawal and Ramakrishnan Srikanth, introduced in their paper, Fast Algorithms for Mining Association Rules. Going forward, we will use both the apriori algorithm and the association rule mining algorithm interchangeably.

We will explain the association rule mining algorithm and the effect of the interest measures on the algorithm as we write our R code. We will halt our code writing in the required places to get a deeper understanding of how the algorithm works, the algorithm terminology such as itemsets, and how to leverage the interest measures to our benefit to support the cross-selling campaign.

We will use the arules package, version 1.5-0, to help us perform association mining on this dataset.

library(arules)
transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = c("order_id", "product_id"),
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")

We begin with reading our transactions stored in the text file and create an arules data structure called transactions. Let's look at the parameters of read.transactions, the function used to create the transactions object. For the first parameter, file, we pass our text file where we have the transactions from the retailer. The second parameter, format, can take any of two values, single or basket, depending on how the input data is organized. In our case, we have a tabular format with two columns--one column representing the unique identifier for our transaction and the other column for a unique identifier representing the product present in our transaction. This format is named single by arules. Refer to the arules documentation for a detailed description of all the parameters.

On inspecting the newly created transactions object transaction.obj:

transactions.obj
transactions in sparse format with
 6988 transactions (rows) and
 16793 items (columns)

We can see that there are 6988 transactions and 16793 products. They match the previous count values from the dplyr output.

Let's explore this transaction object a little bit more. Can we see the most frequent items, that is, the items that are present in most of the transactions and vice versa—the least frequent items and the items present in many fewer transactions?

The itemFrequency function in the arules package comes to our rescue. This function takes a transaction object as input and produces the frequency count (the number of transactions containing this product) of the individual products:

data.frame(head(sort(itemFrequency(transactions.obj, type = "absolute")
 , decreasing = TRUE), 10)) # Most frequent
Banana 1456
 Bag of Organic Bananas 1135
 Organic Strawberries 908
 Organic Baby Spinach 808
 Organic Hass Avocado 729
 Organic Avocado 599
 Large Lemon 534
 Limes 524
 Organic Raspberries 475
 Organic Garlic 432
head(sort(itemFrequency(transactions.obj, type = "absolute")
 , decreasing = FALSE), 10) # Least frequent
0% Fat Black Cherry Greek Yogurt y 1
 0% Fat Blueberry Greek Yogurt 1
 0% Fat Peach Greek Yogurt 1
 0% Fat Strawberry Greek Yogurt 1
 1 % Lowfat Milk 1
 1 Mg Melatonin Sublingual Orange Tablets 1
Razor Handle and 2 Freesia Scented Razor Refills Premium BladeRazor System 1
 1 to 1 Gluten Free Baking Flour 1
 1% Low Fat Cottage Cheese 1
 1% Lowfat Chocolate Milk 1

In the preceding code, we print the most and the least frequent items in our database using the itemFrequency function. The itemFrequency function produces all the items with their corresponding frequency, and the number of transactions in which they appear. We wrap the sort function over itemFrequency to sort this output; the sorting order is decided by the decreasing parameter. When set to TRUE, it sorts the items in descending order based on their transaction frequency. We finally wrap the sort function using the head function to get the top 10 most/least frequent items.

The Banana product is the most frequently occurring across 1,456 transactions. The itemFrequency method can also return the percentage of transactions rather than an absolute number if we set the type parameter to relative instead of absolute.

Another convenient way to inspect the frequency distribution of the items is to plot them visually as a histogram. The arules package provides the itemFrequencyPlot function to visualize the item frequency:

itemFrequencyPlot(transactions.obj,topN = 25)

In the preceding code, we plot the top 25 items by their relative frequency, as shown in the following diagram:

As per the figure, Banana is the most frequent item, present in 20 percent of the transactions. This chart can give us a clue about defining the support value for our algorithm, a concept we will quickly delve into in the subsequent paragraphs.

Now that we have successfully created the transaction object, let's proceed to apply the apriori algorithm to this transaction object.

The apriori algorithm works in two phases. Finding the frequent itemsets is the first phase of the association rule mining algorithm. A group of product IDs is called an itemset. The algorithm makes multiple passes into the database; in the first pass, it finds out the transaction frequency of all the individual items. These are itemsets of order 1. Let's introduce the first interest measure, Support, here:

Now, in the first pass, the algorithm calculates the transaction frequency for each product. At this stage, we have order 1 itemsets. We will discard all those itemsets that fall below our support threshold. The assumption here is that items with a high transaction frequency are more interesting than the ones with a very low frequency. Items with very low support are not going to make for interesting rules further down the pipeline. Using the most frequent items, we can construct the itemsets as having two products and find their transaction frequency, that is, the number of transactions in which both the items are present. Once again, we discard all the two product itemsets (itemsets of order 2) that are below the given support threshold. We continue this way until we have exhausted them.

Let's see a quick illustration:

Pass 1 :

Support = 0.1
Product, transaction frequency
{item5}, 0.4
{item6}, 0.3
{item9}, 0.2
{item11}, 0.1

item11 will be discarded in this phase, as its transaction frequency is below the support threshold.

Pass 2:

{item5, item6}
{item5, item9}
{item6, item9}

As you can see, we have constructed itemsets of order 2 using the filtered items from pass 1. We proceed to find their transaction frequency, discard the itemsets falling below our minimum support threshold, and step on to pass 3, where once again we create itemsets of order 3, calculate the transaction frequency, and perform filtering and move on to pass 4. In one of the subsequent passes, we reach a stage where we cannot create higher order itemsets. That is when we stop:

# Interest Measures
 support <- 0.01
# Frequent item sets
 parameters = list(
 support = support,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "frequent itemsets")
 freq.items <- apriori(transactions.obj, parameter = parameters)

The apriori method is used in arules to get the most frequent items. This method takes two parameters, the transaction.obj and the second parameter, which is a named list. We create a named list called parameters. Inside the named list, we have an entry for our support threshold. We have set our support threshold to 0.01, namely, one percent of the transaction. We settled at this value by looking at the histogram we plotted earlier. By setting the value of the target parameter to frequent itemsets, we specify that we expect the method to return the final frequent itemsets. Minlen and maxlen set lower and upper cut off on how many items we expect in our itemsets. By setting our minlen to 2, we say we don't want itemsets of order 1. While explaining the apriori in phase 1, we said that the algorithm can do many passes into the database, and each subsequent pass creates itemsets that are of order 1, greater than the previous pass. We also said apriori ends when no higher order itemsets can be found. We don't want our method to run till the end, hence by using maxlen, we say that if we reach itemsets of order 10, we stop. The apriori function returns an object of type itemsets.

It's good practice to examine the created object, itemset in this case. A closer look at the itemset object should shed light on how we ended up using its properties to create our data frame of itemsets:

str(freq.items)
Formal class 'itemsets' [package "arules"] with 4 slots
 ..@ items :Formal class 'itemMatrix' [package "arules"] with 3 slots
 .. .. ..@ data :Formal class 'ngCMatrix' [package "Matrix"] with 5 slots
 .. .. .. .. ..@ i : int [1:141] 1018 4107 4767 11508 4767 6543 4767 11187 4767 10322 ...
 .. .. .. .. ..@ p : int [1:71] 0 2 4 6 8 10 12 14 16 18 ...
 .. .. .. .. ..@ Dim : int [1:2] 14286 70
 .. .. .. .. ..@ Dimnames:List of 2
 .. .. .. .. .. ..$ : NULL
 .. .. .. .. .. ..$ : NULL
 .. .. .. .. ..@ factors : list()
 .. .. ..@ itemInfo :'data.frame': 14286 obs. of 1 variable:
 .. .. .. ..$ labels: chr [1:14286] "10" "1000" "10006" "10008" ...
 .. .. ..@ itemsetInfo:'data.frame': 0 obs. of 0 variables
 ..@ tidLists: NULL
 ..@ quality :'data.frame': 70 obs. of 1 variable:
 .. ..$ support: num [1:70] 0.0108 0.0124 0.0124 0.0154 0.0122 ...
 ..@ info :List of 4
 .. ..$ data : symbol transactions.obj
 .. ..$ ntransactions: int 4997
 .. ..$ support : num 0.01
 .. ..$ confidence : num 1

To create our freq.items.df data frame, we used the third slot of the quality freq.items object. It contains the support value for all the itemsets generated, 70 in this case. By calling the function label and passing the freq.items object, we retrieve the item names:

# Let us examine our freq item sites
 freq.items.df <- data.frame(item_set = labels(freq.items)
 , support = freq.items@quality)
head(freq.items.df)

item_set support
1 {Banana,Red Vine Tomato} 0.01030338
2 {Bag of Organic Bananas,Organic D'Anjou Pears} 0.01001717
3 {Bag of Organic Bananas,Organic Kiwi} 0.01016027
4 {Banana,Organic Gala Apples} 0.01073268
5 {Banana,Yellow Onions} 0.01302232

tail(freq.items.df)

item_set support
79 {Organic Baby Spinach,Organic Strawberries} 0.02575844
80 {Bag of Organic Bananas,Organic Baby Spinach} 0.02690326
81 {Banana,Organic Baby Spinach} 0.03048082
82 {Bag of Organic Bananas,Organic Strawberries} 0.03577562
83 {Banana,Organic Strawberries} 0.03305667

We create our data frame using these two lists of values. Finally, we use the head and tail functions to quickly look at the itemsets present at the top and bottom of our data frame.

Before we move on to phase two of the association mining algorithm, let's stop for a moment to investigate a quick feature present in the apriori method. If you had noticed, our itemsets consist mostly of the high frequency itemsets. However, we can ask the apriori method to ignore some of the items:

exclusion.items <- c('Banana','Bag of Organic Bananas')freq.items <- apriori(transactions.obj, parameter = parameters,
 appearance = list(none = exclusion.items,
 default = "both"))

 freq.items.df <- data.frame(item_set = labels(freq.items)
 , support = freq.items@quality)

We can create a vector of items to be excluded, and pass it as an appearance parameter to the apriori method. This will ensure that the items in our list are excluded from the generated itemsets:

head(freq.items.df,10)
item_set support.support support.confidence
 1 {Organic Large Extra Fancy Fuji Apple} => {Organic Strawberries} 0.01030338 0.2727273
 2 {Organic Cilantro} => {Limes} 0.01187750 0.2985612
 3 {Organic Blueberries} => {Organic Strawberries} 0.01302232 0.3063973
 4 {Cucumber Kirby} => {Organic Baby Spinach} 0.01001717 0.2089552
 5 {Organic Grape Tomatoes} => {Organic Baby Spinach} 0.01016027 0.2232704
 6 {Organic Grape Tomatoes} => {Organic Strawberries} 0.01144820 0.2515723
 7 {Organic Lemon} => {Organic Hass Avocado} 0.01016027 0.2184615
 8 {Organic Cucumber} => {Organic Hass Avocado} 0.01244991 0.2660550
 9 {Organic Cucumber} => {Organic Baby Spinach} 0.01144820 0.2446483
 10 {Organic Cucumber} => {Organic Strawberries} 0.01073268 0.2293578

As you can see, we have excluded Banana and Bag of Organic Bananas from our itemsets.

Congratulations, you have successfully finished implementing the first phase of the apriori algorithm in R!

Let's move on to phase two, where we will induce rules from these itemsets. It's time to introduce our second interest measure, confidence. Let's take an itemset from the list given to us from phase one of the algorithm, {Banana, Red Vine Tomato}.

We have two possible rules here:

How often are these two rules found to be true in our database? The confidence score, our next interest measure, will help us measure this:

Similar to support, the confidence threshold is also provided by the user. Only those rules whose confidence is greater than or equal to the user-provided confidence will be included by the algorithm.

With this knowledge, let's go ahead and implement phase two of our apriori algorithm in R:

> confidence <- 0.4 # Interest Measure

 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules"
 )
rules <- apriori(transactions.obj, parameter = parameters)
rules.df <- data.frame(rules = labels(rules)
,rules@quality)

Once again, we use the apriori method; however, we set the target parameter in our parameters named list to rules. Additionally, we also provide the confidence threshold. After calling the method apriori using the returned object rules, we finally build our data frame, rules.df, to explore/view our rules conveniently. Let's look at our output data frame, rules.df. For the given confidence threshold, we can see the set of rules thrown out by the algorithm:

head(rules.df)
rules support confidence lift
 1 {Red Vine Tomato} => {Banana} 0.01030338 0.4067797 1.952319
 2 {Honeycrisp Apple} => {Banana} 0.01617058 0.4248120 2.038864
 3 {Organic Fuji Apple} => {Banana} 0.01817401 0.4110032 1.972590

The last column titled lift is yet another interest measure.

This is where lift comes to our rescue. For two products, A and B, lift measures how many times A and B occur together, more often than expected if they were statistically independent. Let's calculate the lift value for this hypothetical example:

lift ( strawberry => milk ) = support ( strawberry, milk) / support( strawberry) * support (milk)
= 0.3 / (0.9)(0.7)
= 0.47

Lift provides an increased probability of the presence of milk in a transaction containing strawberry. Rules with lift values greater than one are considered to be more effective. In this case, we have a lift value of less than one, indicating that the presence of a strawberry is not going to guarantee the presence of milk in the transaction. Rather, it's the opposite—people who buy strawberries will rarely buy milk in the same transaction.

There are tons of other interest measures available in arules. They can be obtained by calling the  interestMeasure function. We show how we can quickly populate these measures into our rules data frame:

 interestMeasure(rules, transactions = transactions.obj)
rules.df <- cbind(rules.df, data.frame(interestMeasure(rules,
 transactions = transactions.obj)))
 We will not go through all of them here. There is a ton of literature available to discuss these measures and their use in filtering most useful rules.

Alright, we have successfully implemented our association rule mining algorithm; we went under the hood to understand how the algorithm works in two phases to generate rules. We have examined three interest measures: support, confidence, and lift. Finally, we know that lift can be leveraged to make cross-selling recommendations to our retail customers. Before we proceed further, let's look at some more functions in the arules package that will allow us to do some sanity checks on the rules. Let us start with redundant rules:

is.redundant(rules) # Any redundant rules ?

To illustrate redundant rules, let's take an example:

Rule 1: {Red Vine Tomato, Ginger} => {Banana}, confidence score 0.32
Rule 2: {Red Vine Tomato} => {Banana}, confidence score 0.45

Rules 1 and Rule 2 share the same right-hand side, Banana. The left-hand side of Rule 2 has a subset of items from Rule 1. The confidence score of Rule 2  is higher than Rule 1. In this case, Rule 2 is considered a more general rule than Rule 1 and hence Rule 2 will be considered as a redundant rule and removed.  Another sanity check is to find duplicated rules:

duplicated(rules) # Any duplicate rules ?

To remove rules with the same left- and right-hand side, the duplicated function comes in handy. Let's say we create two rules objects, using two sets of support and confidence thresholds. If we combine these two rules objects, we may have a lot of duplicate rules. The duplicated function can be used to filter these duplicate rules. Let us now look at the significance of a rule:

is.significant(rules, transactions.obj, method = "fisher")

Given the rule A => B, we explained that lift calculates how many times A and B occur together more often than expected. There are other ways of testing this independence, like a chi-square test or a Fisher's test. The arules package provides the is.significant method to do a Fisher or a chi-square test of independence. The parameter method can either take the value of fisher or chisq depending on the test we wish to perform. Refer to the arules documentation for more details. Finally let us see  the list of transactions where these rules are supported:

>as(supportingTransactions(rules, transactions.obj), "list")

Here is the complete R script we have used up until now to demonstrate how to leverage arules to extract frequent itemsets, induce rules from those itemsets, and filter the rules based on interest measures.

Here is the following code:

###########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 #
 # RScript to explain how to use arules package
 # to mine Association rules
 #
 # Gopi Subramanian
 ###########################################################################
data.path = '../../data/data.csv' ## Path to data file
data = read.csv(data.path) ## Read the data file
 head(data)
library(dplyr)
 data %>% group_by('order_id') %>% summarize(order.count = n_distinct(order_id))
 data %>% group_by('product_id') %>% summarize(product.count = n_distinct(product_id)
library(arules)
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = c("order_id", "product_id"),
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 transactions.obj
# Item frequency
 head(sort(itemFrequency(transactions.obj, type = "absolute")
 , decreasing = TRUE), 10) # Most frequent
 head(sort(itemFrequency(transactions.obj, type = "absolute")
 , decreasing = FALSE), 10) # Least frequent
itemFrequencyPlot(transactions.obj,topN = 25)
# Interest Measures
 support <- 0.01
# Frequent item sets
 parameters = list(
 support = support,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "frequent itemsets"
 )
freq.items <- apriori(transactions.obj, parameter = parameters)
 # Let us examine our freq item sites
 freq.items.df <- data.frame(item_set = labels(freq.items)
 , support = freq.items@quality)
head(freq.items.df, 5)
 tail(freq.items.df, 5)
# Let us now examine the rules
 confidence <- 0.4 # Interest Measure
 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules"
 )
rules <- apriori(transactions.obj, parameter = parameters)
 rules.df <- data.frame(rules = labels(rules)
 ,rules@quality)
interestMeasure(rules, transactions = transactions.obj)

 rules.df <- cbind(rules.df, data.frame(interestMeasure(rules, transactions = transactions.obj)))
rules.df$coverage <- as(coverage(rules,
 transactions = transactions.obj), "list")
## Some sanity checks
 duplicated(rules) # Any duplicate rules ?
 is.significant(rules, transactions.obj)
## Transactions which support the rule.
 as(supportingTransactions(rules, transactions.obj), "list")

Support and confidence thresholds

It should be clear now that, for our association rule mining algorithm, we need to provide the minimum support and confidence threshold values. Are there are any set guidelines? No, it all depends on the dataset. It would be worthwhile to run a quick experiment to check how many rules are generated for different values of support and confidence. This experiment should give us an idea of what our minimum support/confidence threshold value should be, for the given dataset.

Here is the code for the same:

###########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 # A simple experiment to find support and confidence values
 #
 #
 # Gopi Subramanian
 ###########################################################################

library(ggplot2)
library(arules)

 get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 }

get.rules <- function(support, confidence, transactions){
 # Get Apriori rules for given support and confidence values
 #
 # Args:
 # support: support parameter
 # confidence: confidence parameter
 #
 # Reurns:
 # rules object
 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules")

 rules <- apriori(transactions, parameter = parameters)
 return(rules)
 }

explore.parameters <- function(transactions){
 # Explore support and confidence space for the given transactions
 #
 # Args:
 # transactions: Transaction object, list of transactions
 #
 # Returns:
 # A data frame with no of rules generated for a given
 # support confidence pair.

 support.values <- seq(from = 0.001, to = 0.1, by = 0.001)
 confidence.values <- seq(from = 0.05, to = 0.1, by = 0.01)
 support.confidence <- expand.grid(support = support.values,
 confidence = confidence.values)

 # Get rules for various combinations of support and confidence
 rules.grid <- apply(support.confidence[,c('support','confidence')], 1,
 function(x) get.rules(x['support'], x['confidence'], transactions))

 no.rules <- sapply(seq_along(rules.grid),
 function(i) length(labels(rules.grid[[i]])))

 no.rules.df <- data.frame(support.confidence, no.rules)
 return(no.rules.df)

 }

get.plots <- function(no.rules.df){
 # Plot the number of rules generated for
 # different support and confidence thresholds
 #
 # Args:
 # no.rules.df : data frame of number of rules
 # for different support and confidence
 # values
 #
 # Returns:
 # None

 exp.plot <- function(confidence.value){
 print(ggplot(no.rules.df[no.rules.df$confidence == confidence.value,],
 aes(support, no.rules), environment = environment()) + geom_line()
 + ggtitle(paste("confidence = ", confidence.value)))
 }
 confidence.values <- c(0.07,0.08,0.09,0.1)
 mapply(exp.plot, confidence.value = confidence.values)
 }

columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file

transactions.obj <- get.txn(data.path, columns) ## create txn object
 no.rules.df <- explore.parameters(transactions.obj) ## explore number of rules

head(no.rules.df) ##

get.plots(no.rules.df) ## Plot no of rules vs support

In the preceding code, we show how we can wrap what we have discussed so far into some functions to explore the support and confidence values. The get.rules function conveniently wraps the rule generation functionality. For a given support, confidence, and threshold, this function will return the rules induced by the association rule mining algorithm. The explore.parameters function creates a grid of support and confidence values. You can see that support values are in the range of 0.001 to 0.1, that is, we are exploring the space where items are present in 0.1 percent of the transactions up to 10 percent of the transactions. Finally, the function evaluates the number of rules generated for each support confidence pair in the grid. The function nicely wraps the results in a data frame. For very low support values, we see an extremely large number of rules being generated. Most of them would be spurious rules:

support confidence no.rules
 1 0.001 0.05 23024
 2 0.002 0.05 4788
 3 0.003 0.05 2040
 4 0.004 0.05 1107
 5 0.005 0.05 712
 6 0.006 0.05 512

Analysts can take a look at this data frame, or alternatively plot it to decide the right minimum support/confidence threshold. Our get.plots function plots a number of graphs for different values of confidence. Here is the line plot of the number of rules generated for various support values, keeping the confidence fixed at 0.1:

The preceding plot can be a good guideline for selecting the support value. We generated the preceding plot by fixing the confidence at 10 percent. You can experiment with different values of confidence. Alternatively, use the get.plots function.

Note

The paper, Mining the Most Interesting Rules, by Roberto J. Bayardo Jr. and Rakesh Agrawal demonstrates that the most interesting rules are found on the support/confidence border when we plot the rules with support and confidence on the x and y axes respectively. They call these rules SC-Optimal rules.

Let's get back to our retailer. Let's use what we have built so far to provide recommendations to our retailer for his cross-selling strategy.

This can be implemented using the following code:

###########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 #
 # Script:
 # Generating rules for cross sell campaign.
 #
 #
 # Gopi Subramanian
 ###########################################################################

library(arules)
library(igraph)

get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 } 

get.rules <- function(support, confidence, transactions){
 # Get Apriori rules for given support and confidence values
 #
 # Args:
 # support: support parameter
 # confidence: confidence parameter
 #
 # Returns:
 # rules object
 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules"

 )

 rules <- apriori(transactions, parameter = parameters)
 return(rules)
 }

find.rules <- function(transactions, support, confidence, topN = 10){
 # Generate and prune the rules for given support confidence value
 #
 # Args:
 # transactions: Transaction object, list of transactions
 # support: Minimum support threshold
 # confidence: Minimum confidence threshold
 # Returns:
 # A data frame with the best set of rules and their support and confidence values


 # Get rules for given combination of support and confidence
 all.rules <- get.rules(support, confidence, transactions)

 rules.df <-data.frame(rules = labels(all.rules)
 , all.rules@quality)

 other.im <- interestMeasure(all.rules, transactions = transactions)

 rules.df <- cbind(rules.df, other.im[,c('conviction','leverage')])


 # Keep the best rule based on the interest measure
 best.rules.df <- head(rules.df[order(-rules.df$leverage),],topN)

 return(best.rules.df)
 }

plot.graph <- function(cross.sell.rules){
 # Plot the associated items as graph
 #
 # Args:
 # cross.sell.rules: Set of final rules recommended
 # Returns:
 # None
 edges <- unlist(lapply(cross.sell.rules['rules'], strsplit, split='=>'))

 g <- graph(edges = edges)
 plot(g)

 }

support <- 0.01
confidence <- 0.2

columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file

transactions.obj <- get.txn(data.path, columns) ## create txn object

cross.sell.rules <- find.rules( transactions.obj, support, confidence )
 cross.sell.rules$rules <- as.character(cross.sell.rules$rules)

plot.graph(cross.sell.rules)

After exploring the dataset for support and confidence values, we set the support and confidence values as 0.001 and 0.2 respectively.

We have written a function called find.rules. It internally calls get.rules. This function returns the list of top N rules given the transaction and support/confidence thresholds. We are interested in the top 10 rules. As discussed, we are going to use lift values for our recommendation. The following are our top 10 rules:

  rules support confidence lift conviction leverage
 59 {Organic Hass Avocado} => {Bag of Organic Bananas} 0.03219805 0.3086420 1.900256 1.211498 0.01525399
 63 {Organic Strawberries} => {Bag of Organic Bananas} 0.03577562 0.2753304 1.695162 1.155808 0.01467107
 64 {Bag of Organic Bananas} => {Organic Strawberries} 0.03577562 0.2202643 1.695162 1.115843 0.01467107
 52 {Limes} => {Large Lemon} 0.01846022 0.2461832 3.221588 1.225209 0.01273006
 53 {Large Lemon} => {Limes} 0.01846022 0.2415730 3.221588 1.219648 0.01273006
 51 {Organic Raspberries} => {Bag of Organic Bananas} 0.02318260 0.3410526 2.099802 1.271086 0.01214223
 50 {Organic Raspberries} => {Organic Strawberries} 0.02003434 0.2947368 2.268305 1.233671 0.01120205
 40 {Organic Yellow Onion} => {Organic Garlic} 0.01431025 0.2525253 4.084830 1.255132 0.01080698
 41 {Organic Garlic} => {Organic Yellow Onion} 0.01431025 0.2314815 4.084830 1.227467 0.01080698
 58 {Organic Hass Avocado} => {Organic Strawberries} 0.02432742 0.2331962 1.794686 1.134662 0.01077217

The first entry has a lift value of 1.9, indicating that the products are not independent. This rule has a support of 3 percent and the system has 30 percent confidence for this rule. We recommend that the retailer uses these two products in his cross-selling campaign as, given the lift value, there is a high probability of the customer picking up a {Bag of Organic Bananas} if he picks up an {Organic Hass Avocado}.

Curiously, we have also included two other interest measures—conviction and leverage.

Leverage(A => B) = Support(A => B) - Support(A)*Support(B)

Conviction

Conviction is a measure to ascertain the direction of the rule. Unlike lift, conviction is sensitive to the rule direction. Conviction (A => B) is not the same as conviction (B => A).

For a rule A => B:

conviction ( A => B) = 1 - support(B) / 1 - confidence( A => B)

Conviction, with the sense of its direction, gives us a hint that targeting the customers of Organic Hass Avocado to cross-sell will yield more sales of Bag of Organic Bananas rather than the other way round.

Thus, using lift, leverage, and conviction, we have provided all the empirical details to our retailer to design his cross-selling campaign. In our case, we have recommended the top 10 rules to the retailer based on leverage. To provide the results more intuitively and to indicate what items could go together in a cross-selling campaign, a graph visualization of the rules can be very appropriate.

The plot.graph function is used to visualize the rules that we have shortlisted based on their leverage values. It internally uses a package called igraph to create a graph representation of the rules:

Our suggestion to the retailer can be the largest subgraph on the left. Items in that graph can be leveraged for his cross-selling campaign. Depending on the profit margin and other factors, the retailer can now design his cross-selling campaign using the preceding output.

You were able to provide recommendations to the retailer to design his cross-selling campaign. As you discuss these results with the retailer, you are faced with the following question:

You are shocked; the data scientist in you wants to do everything empirically. Now the retailer is asking for a hard list of products to be added to the campaign. How do you fit them in?

The retailer is insistent: "The products I want to add to the campaign are high margin items. Having them in the campaign will boost my yields."

Voila! The retailer is interested in high-margin items. Let's pull another trick of the trade—weighted association rule mining.

Jubilant, you reply, "Of course I can accommodate these items. Not just them, but also your other high-valued items. I see that you are interested in your margins; can you give me the margin of all your transactions? I can redo the analysis with this additional information and provide you with the new results. Shouldn't take much time."

The retailer is happy. "Of course; here is my margin for the transactions."

Let's introduce weighted association rule mining with an example from the seminal paper, Weighted Association Rules: Models and Algorithms by G.D.Ramkumar et al.

Caviar is an expensive and hence a low support item in any supermarket basket. Vodka, on the other hand, is a high to medium support item. The association, caviar => vodka is of very high confidence but will never be derived by the existing methods as the {caviar, vodka} itemset is of low support and will not be included.

The preceding paragraph echoes our retailer's concern. With the additional information about the margin for our transactions, we can now use weighted association rule mining to arrive at our new set of recommendations:

"transactionID","weight"
 "1001861",0.59502283788534
 "1003729",0.658379205926458
 "1003831",0.635451491097042
 "1003851",0.596453384749423
 "1004513",0.558612727312164
 "1004767",0.557096300448959
 "1004795",0.693775098285732
 "1004797",0.519395513963845
 "1004917",0.581376662057422

The code for the same is as follows:

########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 #
 # RScript to explain weighted Association rule mining
 #
 # Gopi Subramanian
 #########################################################################

library(arules)
 library(igraph)

get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 }

plot.graph <- function(cross.sell.rules){
 # Plot the associated items as graph
 #
 # Args:
 # cross.sell.rules: Set of final rules recommended
 # Returns:
 # None
 edges <- unlist(lapply(cross.sell.rules['rules'], strsplit, split='=>'))

 g <- graph(edges = edges)
 plot(g)

 }

columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file
 transactions.obj <- get.txn(data.path, columns) ## create txn object

# Update the transaction objects
 # with transaction weights
 transactions.obj@itemsetInfo$weight <- NULL
 # Read the weights file
 weights <- read.csv('../../data/weights.csv')
 transactions.obj@itemsetInfo <- weights

# Frequent item set generation
 support <- 0.01

parameters = list(
 support = support,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "frequent itemsets"

 )
 weclat.itemsets <- weclat(transactions.obj, parameter = parameters)

weclat.itemsets.df <-data.frame(weclat.itemsets = labels(weclat.itemsets)
 , weclat.itemsets@quality)

head(weclat.itemsets.df)
 tail(weclat.itemsets.df)

# Rule induction
 weclat.rules <- ruleInduction(weclat.itemsets, transactions.obj, confidence = 0.3)
 weclat.rules.df <-data.frame(rules = labels(weclat.rules)
 , weclat.rules@quality)
 head(weclat.rules.df)

weclat.rules.df$rules <- as.character(weclat.rules.df$rules)
 plot.graph(weclat.rules.df)

In the arules package, the weclat method allows us to use weighted transactions to generate frequent itemsets based on these weights. We introduce the weights through the itemsetinfo data frame in the str(transactions.obj) transactions object:

 Formal class 'transactions' [package "arules"] with 3 slots
 ..@ data :Formal class 'ngCMatrix' [package "Matrix"] with 5 slots
 .. .. ..@ i : int [1:110657] 143 167 1340 2194 2250 3082 3323 3378 3630 4109 ...
 .. .. ..@ p : int [1:6989] 0 29 38 52 65 82 102 125 141 158 ...
 .. .. ..@ Dim : int [1:2] 16793 6988
 .. .. ..@ Dimnames:List of 2
 .. .. .. ..$ : NULL
 .. .. .. ..$ : NULL
 .. .. ..@ factors : list()
 ..@ itemInfo :'data.frame': 16793 obs. of 1 variable:
 .. ..$ labels: chr [1:16793] "#2 Coffee Filters" "0% Fat Black Cherry Greek Yogurt y" "0% Fat Blueberry Greek Yogurt" "0% Fat Free Organic Milk" ...
 ..@ itemsetInfo:'data.frame': 6988 obs. of 1 variable:
 .. ..$ transactionID: chr [1:6988] "1001861" "1003729" "1003831" "1003851" ...

The third slot in the transaction object is a data frame with one column, transactionID. We create a new column called weight in that data frame and push our transaction weights:

weights <- read.csv("../../data/weights.csv")
 transactions.obj@itemsetInfo <- weights
 str(transactions.obj)

In the preceding case, we have replaced the whole data frame. You can either do that or only add the weight column.

Let's now look at the transactions object in the terminal:

Formal class 'transactions' [package "arules"] with 3 slots
 ..@ data :Formal class 'ngCMatrix' [package "Matrix"] with 5 slots
 .. .. ..@ i : int [1:110657] 143 167 1340 2194 2250 3082 3323 3378 3630 4109 ...
 .. .. ..@ p : int [1:6989] 0 29 38 52 65 82 102 125 141 158 ...
 .. .. ..@ Dim : int [1:2] 16793 6988
 .. .. ..@ Dimnames:List of 2
 .. .. .. ..$ : NULL
 .. .. .. ..$ : NULL
 .. .. ..@ factors : list()
 ..@ itemInfo :'data.frame': 16793 obs. of 1 variable:
 .. ..$ labels: chr [1:16793] "#2 Coffee Filters" "0% Fat Black Cherry Greek Yogurt y" "0% Fat Blueberry Greek Yogurt" "0% Fat Free Organic Milk" ...
 ..@ itemsetInfo:'data.frame': 6988 obs. of 2 variables:
 .. ..$ transactionID: int [1:6988] 1001861 1003729 1003831 1003851 1004513 1004767 1004795 1004797 1004917 1004995 ...
 .. ..$ weight : num [1:6988] 0.595 0.658 0.635 0.596 0.559 ...

We have the transactionID and the weight in the itemsetInfo data frame now. Let's run the weighted itemset generation using these transaction weights:

support <- 0.01

parameters = list(
 support = support,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "frequent itemsets"
 )

weclat.itemsets <- weclat(transactions.obj, parameter = parameters)

weclat.itemsets.df <-data.frame(weclat.itemsets = labels(weclat.itemsets)
 , weclat.itemsets@quality

Once again, we invoke the weclat function with the parameter list and the transactions object. As the itemInfo data frame has the weight column, the function calculates the support using the weights provided. The new definition of support is as follows:

For a given item A:

Weighted support ( A ) = Sum of weights of the transactions containing A / Sum of all weights.

The weighted support of an itemset is the sum of the weights of the transactions that contain the itemset. An itemset is frequent if its weighted support is equal to or greater than the threshold specified by support (assuming that the weights, sum is equal to one).

With this new definition, you can see now that low support times established by the old definition of support, if present in high value transactions, will be included. We have automatically taken care of our retailer's request to include high margin items while inducing the rules. Once again, for better reading, we create a data frame where each row is the frequent itemset generated, and a column to indicate the head(weclat.itemsets.df)support value:

  weclat.itemsets support
1 {Bag of Organic Bananas,Organic Kiwi} 0.01041131
2 {Bag of Organic Bananas,Organic D'Anjou Pears} 0.01042194
3 {Bag of Organic Bananas,Organic Whole String Cheese} 0.01034432
4 {Organic Baby Spinach,Organic Small Bunch Celery} 0.01039107
5 {Bag of Organic Bananas,Organic Small Bunch Celery} 0.01109455
6 {Banana,Seedless Red Grapes} 0.01274448

tail(weclat.itemsets.df)

  weclat.itemsets support
77 {Banana,Organic Hass Avocado} 0.02008700
78 {Organic Baby Spinach,Organic Strawberries} 0.02478094
79 {Bag of Organic Bananas,Organic Baby Spinach} 0.02743582
80 {Banana,Organic Baby Spinach} 0.02967578
81 {Bag of Organic Bananas,Organic Strawberries} 0.03626149
82 {Banana,Organic Strawberries} 0.03065132

In the case of apriori, we used the same function to generate/induce the rules. However, in the case of weighted association rule mining, we need to call the ruleInduction function to generate rules. We pass the frequent itemsets from the previous step, the transactions object, and finally the confidence threshold. Once again, for our convenience, we create a data frame with the list of all the rules that are induced and their interest measures:

weclat.rules <- ruleInduction(weclat.itemsets, transactions.obj, confidence = 0.3)
weclat.rules.df <-data.frame(weclat.rules = labels(weclat.rules)
, weclat.rules@quality)

head(weclat.rules.df)

  rules support confidence lift itemset
1 {Organic Kiwi} => {Bag of Organic Bananas} 0.01016027 0.3879781 2.388715 1
3 {Organic D'Anjou Pears} => {Bag of Organic Bananas} 0.01001717 0.3846154 2.368011 2
5 {Organic Whole String Cheese} => {Bag of Organic Bananas} 0.00930166 0.3250000 2.000969 3
11 {Seedless Red Grapes} => {Banana} 0.01302232 0.3513514 1.686293 6
13 {Organic Large Extra Fancy Fuji Apple} => {Bag of Organic Bananas} 0.01445335 0.3825758 2.355453 7
15 {Honeycrisp Apple} => {Banana} 0.01617058 0.4248120 2.038864 8

Finally, let's use the plot.graph function to view the new set of interesting item associations:

Our new recommendation now includes some of the rare items. It is also sensitive to the profit margin of individual transactions. With these recommendations, the retailer is geared toward increasing his profitability through the cross-selling campaign.

In the previous section, we saw that weighted association rule mining leads to recommendations that can increase the profitability of the retailer. Intuitively, weighted association rule mining is superior to vanilla association rule mining as the generated rules are sensitive to transactions, weights. Instead of running the plain version of the algorithm, can we run the weighted association algorithm? We were lucky enough to get transaction weights. What if the retailer did not provide us with the transaction weights? Can we infer weights from transactions? When our transaction data does not come with preassigned weights, we need some way to assign importance to those transactions. For instance, we can say that a transaction with a lot of items should be considered more important than a transaction with a single item.

The arules package provides a method called HITS to help us do the exact same thing—infer transaction weights. HITS stands for Hyperlink-induced Topic Search—a link analysis algorithm used to rate web pages developed by John Kleinberg. According to HITS, hubs are pages with large numbers of out degrees and authority are pages with large numbers of in degrees.

The rationale is that if a lot of pages link to a particular page, then that page is considered an authority. If a page has links to a lot of other pages, it is considered a hub.

The basic idea behind using the HITS algorithm for association rule mining is that frequent items may not be as important as they seem. The paper presents an algorithm that applies the HITS methodology to bipartite graphs.

According to the HITS modified for the transactions database, the transactions and products are treated as a bipartite graph, with an arc going from the transaction to the product if the product is present in the transaction. The following diagram is reproduced from the paper, Mining Weighted Association Rules without Preassigned Weights by Ke Sun and Fengshan Bai, to illustrate how transactions in a database are converted to a bipartite graph:

In this representation, the transactions can be ranked using the HITS algorithm. In this kind of representation, the support of an item is proportional to its degree. Consider item A. Its absolute support is 4; in the graph, the in degree of A is four. As you can see, considering only the support, we totally ignore transaction importance, unless the importance of the transactions is explicitly provided. How do we get the transaction weights in this scenario? Again, a way to get the weights intuitively is from a good transaction, which should be highly weighted and should contain many good items. A good item should be contained by many good transactions. By treating transactions as hubs and the products as authorities, the algorithm invokes HITS on this bipartite graph.

The arules package provides the method (HITS), which implements the algorithm that we described earlier:

weights.vector <- hits( transactions.obj, type = "relative")
weights.df <- data.frame(transactionID = labels(weights.vector), weight = weights.vector)

We invoke the algorithm using the HITS method. We have described the intuition behind using the HITS algorithm in transaction databases to give weights to our transactions. We will briefly describe how the HITS algorithm functions. Curious readers can refer to Authoritative Sources in a Hyperlinked Environment, J.M. Kleinberg, J. ACM, vol. 46, no. 5, pp. 604-632, 1999, for a better understanding of the HITS algorithm.

The HITS algorithm, to begin with, initializes the weight of all nodes to one; in our case, the items and the transactions are set to one. That is, we maintain two arrays, one for hub weights and the other one for authority weights.

It proceeds to do the following three steps in an iterative manner, that is, until our hub and authority arrays stabilize or don't change with subsequent updates:

At the end of the algorithm, every item has an authority score, which is the sum of the hub scores of all the transactions that contain this item. Every transaction has a hub score that is the sum of the authority score of all the items in that transaction. Using the weights created using the HITS algorithm, we create a weights.df data frame:

head(weights.df)

                transactionID weight
1000431 1000431 1.893931e-04
100082 100082 1.409053e-04
1000928 1000928 2.608214e-05
1001517 1001517 1.735461e-04
1001650 1001650 1.184581e-04
1001934 1001934 2.310465e-04

Pass weights.df our transactions object. We can now generate the weighted association rules:

transactions.obj@itemsetInfo <- weights.df

support <- 0.01
 parameters = list(
 support = support,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "frequent itemsets"

 )
 weclat.itemsets <- weclat(transactions.obj, parameter = parameters)
 weclat.itemsets.df <-data.frame(weclat.itemsets = labels(weclat.itemsets)
 , weclat.itemsets@quality)

weclat.rules <- ruleInduction(weclat.itemsets, transactions.obj, confidence = 0.1)
 weclat.rules.df <-data.frame(weclat.rules = labels(weclat.rules)
 , weclat.rules@quality)

We can look into the output data frames created for frequent itemsets and rules:

head(weclat.itemsets.df)

  weclat.itemsets support
1 {Banana,Russet Potato} 0.01074109
2 {Banana,Total 0% Nonfat Greek Yogurt} 0.01198206
3 {100% Raw Coconut Water,Bag of Organic Bananas} 0.01024201
4 {Organic Roasted Turkey Breast,Organic Strawberries} 0.01124278
5 {Banana,Roma Tomato} 0.01089124
6 {Banana,Bartlett Pears} 0.01345293

tail(weclat.itemsets.df)

  weclat.itemsets support
540 {Bag of Organic Bananas,Organic Baby Spinach,Organic Strawberries} 0.02142840
541 {Banana,Organic Baby Spinach,Organic Strawberries} 0.02446832
542 {Bag of Organic Bananas,Organic Baby Spinach} 0.06536606
543 {Banana,Organic Baby Spinach} 0.07685530
544 {Bag of Organic Bananas,Organic Strawberries} 0.08640422
545 {Banana,Organic Strawberries} 0.08226264

head(weclat.rules.df)

weclat.rules support confidence lift itemset
weclat.rules support confidence lift itemset
1 {Russet Potato} => {Banana} 0.005580996 0.3714286 1.782653 1
3 {Total 0% Nonfat Greek Yogurt} => {Banana} 0.005580996 0.4148936 1.991261 2
6 {100% Raw Coconut Water} => {Bag of Organic Bananas} 0.004865484 0.3238095 1.993640 3
8 {Organic Roasted Turkey Breast} => {Organic Strawberries} 0.004579279 0.3440860 2.648098 4
9 {Roma Tomato} => {Banana} 0.006010303 0.3181818 1.527098 5
11 {Bartlett Pears} => {Banana} 0.007870635 0.4545455 2.181568 6

Based on the weights generated using the HITS algorithm, we can now order the items by their authority score. This is an alternate way of ranking the items in addition to ranking them by their frequency. We can leverage the itemFrequency function to generate the item scores:

freq.weights <- head(sort(itemFrequency(transactions.obj, weighted = TRUE),decreasing = TRUE),20)
freq.nweights <- head(sort(itemFrequency(transactions.obj, weighted = FALSE),decreasing = TRUE),20)

compare.df <- data.frame("items" = names(freq.weights),
"score" = freq.weights,
"items.nw" = names(freq.nweights),
"score.nw" = freq.nweights)
row.names(compare.df) <- NULL

Let's look at the compare.dfdata frame:

The column score gives the relative transaction frequency. The score.new column is the authority score from the hits algorithm. You can see that Limes and Large Lemon have interchanged places. Strawberries has gone further up the order compared to the original transaction frequency score.

The code is as follows:

###############################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 #
 # RScript to explain application of hits to
 # transaction database.
 #
 # Gopi Subramanian
 ###############################################################################

library(arules)

get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 }

## Create txn object
 columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file
 transactions.obj <- get.txn(data.path, columns) ## create txn object

## Generate weight vector using hits
 weights.vector <- hits( transactions.obj, type = "relative")
 weights.df <- data.frame(transactionID = labels(weights.vector), weight = weights.vector)

head(weights.df)

transactions.obj@itemsetInfo <- weights.df

## Frequent item sets generation
 support <- 0.01
 parameters = list(
 support = support,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "frequent itemsets"

 )
 weclat.itemsets <- weclat(transactions.obj, parameter = parameters)
 weclat.itemsets.df <-data.frame(weclat.itemsets = labels(weclat.itemsets)
 , weclat.itemsets@quality)

head(weclat.itemsets.df)
 tail(weclat.itemsets.df)

## Rule induction
 weclat.rules <- ruleInduction(weclat.itemsets, transactions.obj, confidence = 0.3)
 weclat.rules.df <-data.frame(weclat.rules = labels(weclat.rules)
 , weclat.rules@quality)

head(weclat.rules.df)

freq.weights <- head(sort(itemFrequency(transactions.obj, weighted = TRUE),decreasing = TRUE),20)
 freq.nweights <- head(sort(itemFrequency(transactions.obj, weighted = FALSE),decreasing = TRUE),20)

compare.df <- data.frame("items" = names(freq.weights),
 "score" = freq.weights,
 "items.nw" = names(freq.nweights),
 "score.nw" = freq.nweights)
 row.names(compare.df) <- NULL

Throughout, we have been focusing on inducing rules indicating the chance of an item being added to the basket, given that there are other items present in the basket. However, knowing the relationship between the absence of an item and the presence of another in the basket can be very important in some applications. These rules are called negative association rules. The association bread implies milk indicates the purchasing behavior of buying milk and bread together. What about the following associations: customers who buy tea do not buy coffee, or customers who buy juice do not buy bottled water? Associations that include negative items (that is, items absent from the transaction) can be as valuable as positive associations in many scenarios, such as when devising marketing strategies for promotions.

There are several algorithms proposed to induce negative association rules from a transaction database. Apriori is not a well-suited algorithm for negative association rule mining. In order to use apriori, every transaction needs to be updated with all the items—those that are present in the transaction and those that are absent. This will heavily inflate the database. In our case, every transaction will have 16,000 items. We can cheat; we can leverage the use of apriori for negative association rule mining only for a selected list of items. In transactions that do not contain the item, we can create an entry for that item to indicate that the item is not present in the transaction. The arules package's function, addComplement, allows us to do exactly that.

Let's say that our transaction consists of the following:

Banana, Strawberries
Onions, ginger, garlic
Milk, Banana

When we pass this transaction to addComplement and say that we want non-Banana entries to be added to the transaction, the resulting transaction from addComplement will be as follows:

Banana, Strawberries
Onions, ginger, garlic, !Banana
Milk, Banana

An exclamation mark is the standard way to indicate the absence; however, you can choose your own prefix:

get.neg.rules <- function(transactions, itemList, support, confidence){
 # Generate negative association rules for given support confidence value
 #
 # Args:
 # transactions: Transaction object, list of transactions
 # itemList : list of items to be negated in the transactions
 # support: Minimum support threshold
 # confidence: Minimum confidence threshold
 # Returns:
 # A data frame with the best set negative rules and their support and confidence values

 neg.transactions <- addComplement( transactions.obj, labels = itemList)
 rules <- find.rules(neg.transactions, support, confidence)
 return(rules)
 }

In the preceding code, we have created a get.neg.rules function. Inside this method, we have leveraged the addComplement function to introduce the absence entry of the given items in itemList into the transactions. We generate the rules with the newly formed transactions, neg.transactions:

itemList <- c("Organic Whole Milk","Cucumber Kirby")
neg.rules <- get.neg.rules(transactions.obj,itemList, .05,.6)

 neg.rules.nr <- neg.rules[!is.redundant(neg.rules)]
 labels(neg.rules.nr)

Once we have the negative rules, we pass those through is.redundant to remove any redundant rules and finally print the rules:

[1] "{Strawberries} => {!Organic Whole Milk}"
[2] "{Strawberries} => {!Cucumber Kirby}"
[3] "{Organic Whole Milk} => {!Cucumber Kirby}"
[4] "{Organic Zucchini} => {!Cucumber Kirby}"
[5] "{Organic Yellow Onion} => {!Organic Whole Milk}"
[6] "{Organic Yellow Onion} => {!Cucumber Kirby}"
[7] "{Organic Garlic} => {!Organic Whole Milk}"
[8] "{Organic Garlic} => {!Cucumber Kirby}"
[9] "{Organic Raspberries} => {!Organic Whole Milk}"
[10] "{Organic Raspberries} => {!Cucumber Kirby}"

The code is as follows:

########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 #
 # RScript to explain negative associative rule mining
 #
 # Gopi Subramanian
 #########################################################################

library(arules)
 library(igraph)

get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 }

get.rules <- function(support, confidence, transactions){
 # Get Apriori rules for given support and confidence values
 #
 # Args:
 # support: support parameter
 # confidence: confidence parameter
 #
 # Returns:
 # rules object
 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules"

 )

 rules <- apriori(transactions, parameter = parameters)
 return(rules)
 }
 get.neg.rules <- function(transactions, itemList, support, confidence){
 # Generate negative association rules for given support confidence value
 #
 # Args:
 # transactions: Transaction object, list of transactions
 # itemList : list of items to be negated in the transactions
 # support: Minimum support threshold
 # confidence: Minimum confidence threshold
 # Returns:
 # A data frame with the best set negative rules and their support and confidence values
 neg.transactions <- addComplement( transactions, labels = itemList)
 rules <- get.rules(support, confidence, neg.transactions)
 return(rules)
 }

columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file

transactions.obj <- get.txn(data.path, columns) ## create txn object

itemList <- c("Organic Whole Milk","Cucumber Kirby")

neg.rules <- get.neg.rules(transactions.obj,itemList, support = .05,
 confidence = .6)

neg.rules.nr <- neg.rules[!is.redundant(neg.rules)]

labels(neg.rules.nr)

In the previous sections, we leveraged plotting capability from the arules and igraph packages to plot induced rules. In this section, we introduce arulesViz, a package dedicated to plot association rules, generated by the arules package. The arulesViz package integrates seamlessly with the arules packages in terms of sharing data structures.

The following code is quite self-explanatory. A multitude of graphs, including interactive/non-interactive scatter plots, graph plots, matrix plots, and group plots can be generated from the rules data structure; it's a great visual way to explore the rules induced:

########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 #
 # RScript to explore arulesViz package
 # for Association rules visualization
 #
 # Gopi Subramanian
 #########################################################################

library(arules)
 library(arulesViz)

get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 }

get.rules <- function(support, confidence, transactions){
 # Get Apriori rules for given support and confidence values
 #
 # Args:
 # support: support parameter
 # confidence: confidence parameter
 #
 # Returns:
 # rules object
 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules"

 )

 rules <- apriori(transactions, parameter = parameters)
 return(rules)

support <- 0.01
 confidence <- 0.2

# Create transactions object
 columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file
 transactions.obj <- get.txn(data.path, columns) ## create txn object

# Induce Rules
 all.rules <- get.rules(support, confidence, transactions.obj)

# Scatter plot of rules
 plotly_arules(all.rules, method = "scatterplot", measure = c("support","lift"), shading = "order")

# Interactive scatter plots
 plot(all.rules, method = NULL, measure = "support", shading = "lift", interactive = TRUE)

# Get top rules by lift
 sub.rules <- head(sort(all.rules, by="lift"), 15

# Group plot of rules
 plot(sub.rules, method="grouped")

# Graph plot of rule
 plot(sub.rules, method="graph", measure = "lift")

The following diagram is the scatter plot of rules induced:

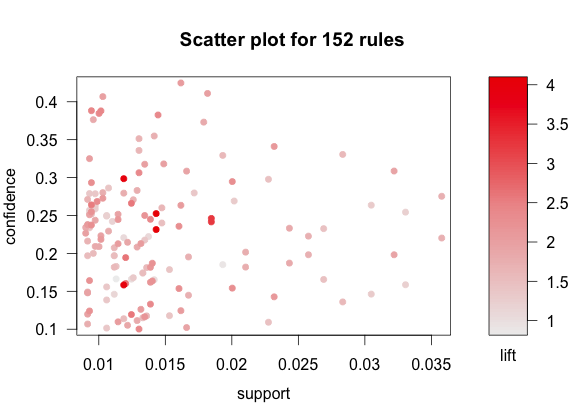
The following diagram is the grouped plot of rules induced:

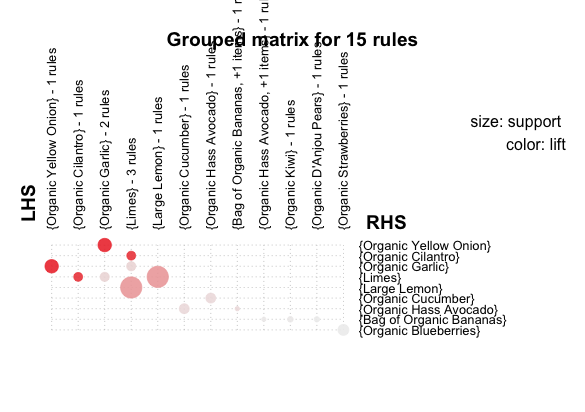
The following diagram is the graph plot of rules induced:

The final step in any data analysis project is documentation—either generating a report of the findings or documenting the scripts and data used. In our case, we are going to wrap up with a small application. We will use RShiny, an R web application framework. RShiny is a powerful framework for developing interactive web applications using R. We will leverage the code that we have written to generate a simple, yet powerful, user interface for our retail customers.

To keep things simple, we have a set of three screens. The first screen, as shown in the following screenshot, allows the user to vary support and confidence thresholds and view the rules generated. It also has additional interest measures, lift, conviction, and leverage. The user can sort the rule by any of these interest measures:

Another screen is a scatter plot representation of the rules:

Finally, a graph representation to view the product grouping for the easy selection of products for the cross-selling campaign is as follows:

The complete source code is available in <../App.R>:

########################################################################
 #
 # R Data Analysis Projects
 #
 # Chapter 1
 #
 # Building Recommender System
 # A step step approach to build Association Rule Mining
 #
 # Script:
 #
 # Rshiny app
 #
 # Gopi Subramanian
 #########################################################################

library(shiny)
 library(plotly)
 library(arules)
 library(igraph)
 library(arulesViz)

get.txn <- function(data.path, columns){
 # Get transaction object for a given data file
 #
 # Args:
 # data.path: data file name location
 # columns: transaction id and item id columns.
 #
 # Returns:
 # transaction object
 transactions.obj <- read.transactions(file = data.path, format = "single",
 sep = ",",
 cols = columns,
 rm.duplicates = FALSE,
 quote = "", skip = 0,
 encoding = "unknown")
 return(transactions.obj)
 }

get.rules <- function(support, confidence, transactions){
 # Get Apriori rules for given support and confidence values
 #
 # Args:
 # support: support parameter
 # confidence: confidence parameter
 #
 # Returns:
 # rules object
 parameters = list(
 support = support,
 confidence = confidence,
 minlen = 2, # Minimal number of items per item set
 maxlen = 10, # Maximal number of items per item set
 target = "rules"

 )

 rules <- apriori(transactions, parameter = parameters)
 return(rules)
 }

find.rules <- function(transactions, support, confidence, topN = 10){
 # Generate and prune the rules for given support confidence value
 #
 # Args:
 # transactions: Transaction object, list of transactions
 # support: Minimum support threshold
 # confidence: Minimum confidence threshold
 # Returns:
 # A data frame with the best set of rules and their support and confidence values


 # Get rules for given combination of support and confidence
 all.rules <- get.rules(support, confidence, transactions)

 rules.df <-data.frame(rules = labels(all.rules)
 , all.rules@quality)

 other.im <- interestMeasure(all.rules, transactions = transactions)

 rules.df <- cbind(rules.df, other.im[,c('conviction','leverage')])


 # Keep the best rule based on the interest measure
 best.rules.df <- head(rules.df[order(-rules.df$leverage),],topN)

 return(best.rules.df)
 }

plot.graph <- function(cross.sell.rules){
 # Plot the associated items as graph
 #
 # Args:
 # cross.sell.rules: Set of final rules recommended
 # Returns:
 # None
 edges <- unlist(lapply(cross.sell.rules['rules'], strsplit, split='=>'))
 g <- graph(edges = edges)
 return(g)

 }

columns <- c("order_id", "product_id") ## columns of interest in data file
 data.path = '../../data/data.csv' ## Path to data file
 transactions.obj <- get.txn(data.path, columns) ## create txn object

server <- function(input, output) {

cross.sell.rules <- reactive({
 support <- input$Support
 confidence <- input$Confidence
 cross.sell.rules <- find.rules( transactions.obj, support, confidence )
 cross.sell.rules$rules <- as.character(cross.sell.rules$rules)
 return(cross.sell.rules)

 })

 gen.rules <- reactive({
 support <- input$Support
 confidence <- input$Confidence
 gen.rules <- get.rules( support, confidence ,transactions.obj)
 return(gen.rules)

 })


 output$rulesTable <- DT::renderDataTable({
 cross.sell.rules()
 })

 output$graphPlot <- renderPlot({
 g <-plot.graph(cross.sell.rules())
 plot(g)
 })

 output$explorePlot <- renderPlot({
 plot(x = gen.rules(), method = NULL,
 measure = "support",
 shading = "lift", interactive = FALSE)
 })


 }

ui <- fluidPage(
 headerPanel(title = "X-Sell Recommendations"),
 sidebarLayout(
 sidebarPanel(
 sliderInput("Support", "Support threshold:", min = 0.01, max = 1.0, value = 0.01),
 sliderInput("Confidence", "Support threshold:", min = 0.05, max = 1.0, value = 0.05)

 ),
 mainPanel(
 tabsetPanel(
 id = 'xsell',
 tabPanel('Rules', DT::dataTableOutput('rulesTable')),
 tabPanel('Explore', plotOutput('explorePlot')),
 tabPanel('Item Groups', plotOutput('graphPlot'))
 )
 )
 )
 )

shinyApp(ui = ui, server = server)

We have described the get.txn, get.rules, and find.rules functions in the previous section. We will not go through them again here. The preceding code is a single page RShiny app code; both the server and the UI component reside in the same file.

The UI component is as follows:

ui <- fluidPage(
 headerPanel(title = "X-Sell Recommendations"),
 sidebarLayout(
 sidebarPanel(
 sliderInput("Support", "Support threshold:", min = 0.01, max = 1.0, value = 0.01),
 sliderInput("Confidence", "Support threshold:", min = 0.05, max = 1.0, value = 0.05)

 ),
 mainPanel(
 tabsetPanel(
 id = 'xsell',
 tabPanel('Rules', DT::dataTableOutput('rulesTable')),
 tabPanel('Explore', plotOutput('explorePlot')),
 tabPanel('Item Groups', plotOutput('graphPlot'))
 )
 )
 )
 )

We define the screen layout in this section. This section can also be kept in a separate file called UI.R. The page is defined by two sections, a panel in the left, defined by sidebarPanel, and a main section defined under mainPanel. Inside the side bar, we have defined two slider controls for the support and confidence thresholds respectively. The main panel contains a tab-separated window, defined by tabPanel.

The main panel has three tabs; each tab has a slot defined for the final set of rules, with their interest measures, a scatter plot for the rules, and finally the graph plot of the rules.

The server component is as follows:

server <- function(input, output) {

cross.sell.rules <- reactive({
 support <- input$Support
 confidence <- input$Confidence
 cross.sell.rules <- find.rules( transactions.obj, support, confidence )
 cross.sell.rules$rules <- as.character(cross.sell.rules$rules)
 return(cross.sell.rules)

 })

The cross.sell.rules data frame is defined as a reactive component. When the values of the support and confidence thresholds change in the UI, cross.sell.rules data frame will be recomputed. This frame will be served to the first page, where we have defined a slot for this table, called rulesTable:

gen.rules <- reactive({
 support <- input$Support
 confidence <- input$Confidence
 gen.rules <- get.rules( support, confidence ,transactions.obj)
 return(gen.rules)
 })

This reactive component retrieves the calculations and returns the rules object every time the support or/and confidence threshold is changed by the user in the UI:

output$rulesTable <- DT::renderDataTable({
 cross.sell.rules()
 })

The preceding code renders the data frame back to the UI:

output$graphPlot <- renderPlot({
 g <-plot.graph(cross.sell.rules())
 plot(g)
 })

 output$explorePlot <- renderPlot({
 plot(x = gen.rules(), method = NULL,
 measure = "support",
 shading = "lift", interactive = FALSE)
 })


 }

The preceding two pieces of code render the plot back to the UI.

We started the chapter with an overview of recommender systems. We introduced our retail case and the association rule mining algorithm. Then we applied association rule mining to design a cross-selling campaign. We went on to understand weighted association rule mining and its applications. Following that, we introduced the HITS algorithm and its use in transaction data. Next, we studied the negative association rules discovery process and its use. We showed you different ways to visualize association rules. Finally, we created a small web application using R Shiny to demonstrate some of the concepts we learned.

In the next chapter, we will look at another recommendation system algorithm called content based filtering. We will see how this method can help address the famous cold start problem in recommendation systems. Furthermore, we will introduce the concept of fuzzy ranking to order the final recommendations.