In Wright's model, the learning curve function is defined as follows:
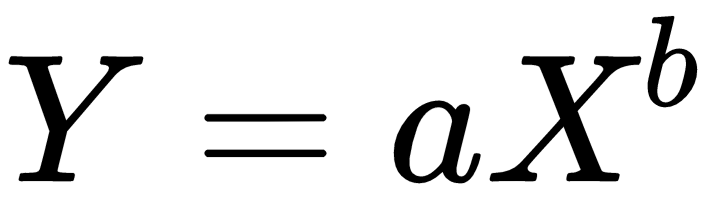
The variables are as follows:
- Y: The cumulative average time per unit
- X: The cumulative number of units produced
- a: Time required to produce the first unit
- b: Slope of the function when plotted on graph paper (log of the learning rate/log of 2)
The following curve has got a vertical axis (y axis) representing the learning with respect to a particular work and a horizontal axis that corresponds to the time taken to learn. A learning curve with a steep beginning can be comprehended as a sign of rapid progress. The following diagram shows Wright's Learning Curve Model:
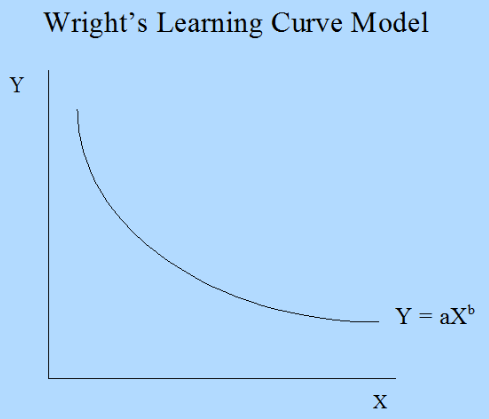
However, the question that arises is, How is it connected to machine learning? We will discuss this in detail now.
Let's discuss a scenario that happens to be a supervised learning problem by going over the following steps:
- We take the data and partition it into a training set (on which we are making the system learn and come out as a model) and a validation set (on which we are testing how well the system has learned).
- The next step would be to take one instance (observation) of the training set and make use of it to estimate a model. The model error on the training set will be 0.
- Finally, we would find out the model error on the validation data.
Step 2 and Step 3 are repeated by taking a number of instances (training size) such as 10, 50, and 100 and studying the training error and validation error, as well as their relationship with a number of instances (training size). This curve—or the relationship—is called a learning curve in a machine learning scenario.
Let's work on a combined power plant dataset. The features comprised hourly average ambient variables, that is, temperature (T), ambient pressure (AP), relative humidity (RH), and exhaust vacuum (V), to predict the net hourly electrical energy output (PE) of the plant:
# importing all the libraries
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
#reading the data
data= pd.read_excel("Powerplant.xlsx")
#Investigating the data
print(data.info())
data.head()
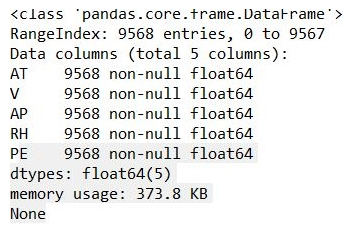
From this, we are able to see the data structure of the variables in the data:
The output can be seen as follows:
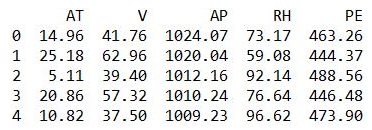
The second output gives you a good feel for the data.
The dataset has five variables, where ambient temperature (AT) and PE (target variable).
Let's vary the training size of the data and study the impact of it on learning. A list is created for train_size with varying training sizes, as shown in the following code:
# As discussed here we are trying to vary the size of training set
train_size = [1, 100, 500, 2000, 5000]
features = ['AT', 'V', 'AP', 'RH']
target = 'PE'
# estimating the training score & validation score
train_sizes, train_scores, validation_scores = learning_curve(estimator = LinearRegression(), X = data[features],y = data[target], train_sizes = train_size, cv = 5,scoring ='neg_mean_squared_error')
Let's generate the learning_curve:
# Generating the Learning_Curve
train_scores_mean = -train_scores.mean(axis = 1)
validation_scores_mean = -validation_scores.mean(axis = 1)
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.plot(train_sizes, train_scores_mean, label = 'Train_error')
plt.plot(train_sizes, validation_scores_mean, label = 'Validation_error')
plt.ylabel('MSE', fontsize = 16)
plt.xlabel('Training set size', fontsize = 16)
plt.title('Learning_Curves', fontsize = 20, y = 1)
plt.legend()
We get the following output:
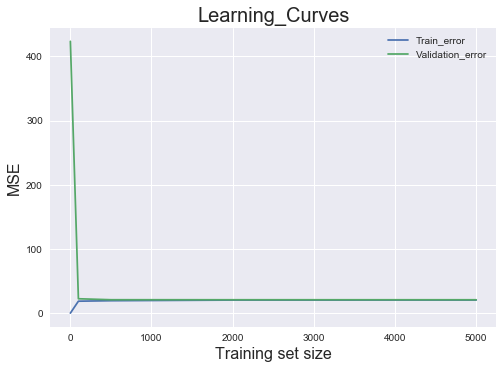
From the preceding plot, we can see that when the training size is just 1, the training error is 0, but the validation error shoots beyond 400.
As we go on increasing the training set's size (from 1 to 100), the training error continues rising. However, the validation error starts to plummet as the model performs better on the validation set. After the training size hits the 500 mark, the validation error and training error begin to converge. So, what can be inferred out of this? The performance of the model won't change, irrespective of the size of the training post. However, if you try to add more features, it might make a difference, as shown in the following diagram:
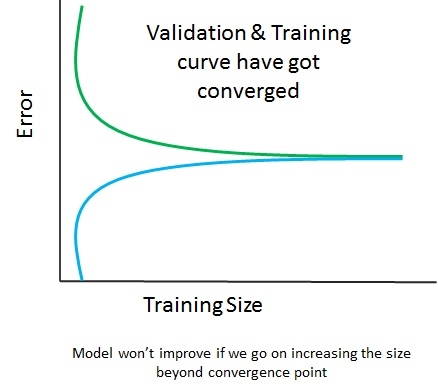
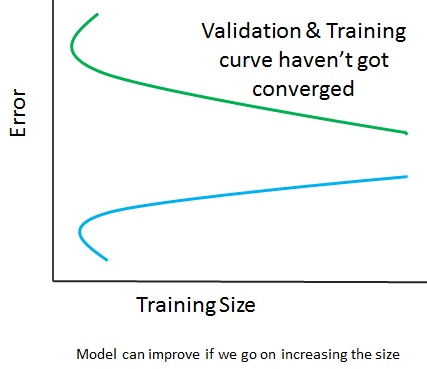
The preceding diagram shows that the validation and training curve have converged, so adding training data will not help at all. However, in the following diagram, the curves haven't converged, so adding training data will be a good idea:
 United States
United States
 Great Britain
Great Britain
 India
India
 Germany
Germany
 France
France
 Canada
Canada
 Russia
Russia
 Spain
Spain
 Brazil
Brazil
 Australia
Australia
 Singapore
Singapore
 Canary Islands
Canary Islands
 Hungary
Hungary
 Ukraine
Ukraine
 Luxembourg
Luxembourg
 Estonia
Estonia
 Lithuania
Lithuania
 South Korea
South Korea
 Turkey
Turkey
 Switzerland
Switzerland
 Colombia
Colombia
 Taiwan
Taiwan
 Chile
Chile
 Norway
Norway
 Ecuador
Ecuador
 Indonesia
Indonesia
 New Zealand
New Zealand
 Cyprus
Cyprus
 Denmark
Denmark
 Finland
Finland
 Poland
Poland
 Malta
Malta
 Czechia
Czechia
 Austria
Austria
 Sweden
Sweden
 Italy
Italy
 Egypt
Egypt
 Belgium
Belgium
 Portugal
Portugal
 Slovenia
Slovenia
 Ireland
Ireland
 Romania
Romania
 Greece
Greece
 Argentina
Argentina
 Netherlands
Netherlands
 Bulgaria
Bulgaria
 Latvia
Latvia
 South Africa
South Africa
 Malaysia
Malaysia
 Japan
Japan
 Slovakia
Slovakia
 Philippines
Philippines
 Mexico
Mexico
 Thailand
Thailand














