Among all the predictions that were made about the 21st century, maybe the most unexpected one was that we would collect such a formidable amount of data about everything, everyday, and everywhere in the world. Recent years have seen an incredible explosion of data collection about our world, our lives, and technology; this is the main driver of what we can certainly call a revolution. We live in the Age of Information. But collecting data is nothing if we don't exploit it and try to extract knowledge out of it.
At the beginning of the 20th century, with the birth of statistics, the world was all about collecting data and making statistics. In that time, the only reliable tools were pencils and paper and of course, the eyes and ears of the observers. Scientific observation was still in its infancy, despite the prodigious development of the 19th century.
More than a hundred years later, we have computers, we have electronic sensors, we have massive data storage and we are able to store huge amounts of data continuously about, not only our physical world, but also our lives, mainly through the use of social networks, the Internet, and mobile phones. Moreover, the density of our storage technology has increased so much that we can, nowadays, store months if not years of data into a very small volume that can fit in the palm of our hand.
But storing data is not acquiring knowledge. Storing data is just keeping it somewhere for future use. At the same time as our storage capacity dramatically evolved, the capacity of modern computers increased too, at a pace that is sometimes hard to believe. When I was a doctoral student, I remember how proud I was when in the laboratory I received that brand-new, shiny, all-powerful PC for carrying my research work. Today, my old smart phone, which fits in my pocket, is more than 20 times faster.
Therefore in this book, you will learn one of the most advanced techniques to transform data into knowledge: machine learning. This technology is used in every aspect of modern life now, from search engines, to stock market predictions, from speech recognition to autonomous vehicles. Moreover it is used in many fields where one would not suspect it at all, from quality assurance in product chains to optimizing the placement of antennas for mobile phone networks.
Machine learning is the marriage between computer science and probabilities and statistics. A central theme in machine learning is the problem of inference or how to produce knowledge or predictions using an algorithm fed with data and examples. And this brings us to the two fundamental aspects of machine learning: the design of algorithms that can extract patterns and high-level knowledge from vast amounts of data and also the design of algorithms that can use this knowledge—or, in scientific terms: learning and inference.
Pierre-Simon Laplace (1749-1827) a French mathematician and one of the greatest scientists of all time, was presumably among the first to understand an important aspect of data collection: data is unreliable, uncertain and, as we say today, noisy. He was also the first to develop the use of probabilities to deal with such aspects of uncertainty and to represent one's degree of belief about an event or information.
In his Essai philosophique sur les probabilités (1814), Laplace formulated an original mathematical system for reasoning about new and old data, in which one's belief about something could be updated and improved as soon as new data where available. Today we call that Bayesian reasoning. Indeed Thomas Bayes was the first, toward the end of the 18th century, to discover this principle. Without any knowledge about Bayes' work, Pierre-Simon Laplace rediscovered the same principle and formulated the modern form of the Bayes theorem. It is interesting to note that Laplace eventually learned about Bayes' posthumous publications and acknowledged Bayes to be the first to describe the principle of this inductive reasoning system. Today, we speak about Laplacian reasoning instead of Bayesian reasoning and we call it the Bayes-Price-Laplace theorem.
More than a century later, this mathematical technique was reborn thanks to new discoveries in computing probabilities and gave birth to one of the most important and used techniques in machine learning: the probabilistic graphical model.
From now on, it is important to note that the term graphical refers to the theory of graphs—that is, a mathematical object with nodes and edges (and not graphics or drawings). You know that, when you want to explain to someone the relationships between different objects or entities, you take a sheet of paper and draw boxes that you connect with lines or arrows. It is an easy and neat way to show relationships, whatever they are, between different elements.
Probabilistic Graphical Models (PGM for short) are exactly that: you want to describe relationships between variables. However, you don't have any certainty about your variables, but rather beliefs or uncertain knowledge. And we know now that probabilities are the way to represent and deal with such uncertainties, in a mathematical and rigorous way.
A probabilistic graphical model is a tool to represent beliefs and uncertain knowledge about facts and events using probabilities. It is also one of the most advanced machine learning techniques nowadays and has many industrial success stories.
Probabilistic graphical models can deal with our imperfect knowledge about the world because our knowledge is always limited. We can't observe everything, we can't represent all the universe in a computer. We are intrinsically limited as human beings, as are our computers. With probabilistic graphical models, we can build simple learning algorithms or complex expert systems. With new data, we can improve those models and refine them as much as we can and also we can infer new information or make predictions about unseen situations and events.
In this first chapter you will learn about the fundamentals needed to understand probabilistic graphical models; that is, probabilities and the simple rules of calculus on which they are based. We will have an overview of what we can do with probabilistic graphical models and the related R packages. These techniques are so successful that we will have to restrict ourselves to just the most important R packages.
We will see how to develop simple models, piece by piece, like a brick game and how to connect models together to develop even more advanced expert systems. We will cover the following concepts and applications and each section will contain numerical examples that you can directly use with R:
Machine learning
Representing uncertainty with probabilities
Notions of probabilistic expert systems
Representing knowledge with graphs
Probabilistic graphical models
Examples and applications
This book is about a field of science called machine learning, or more generally artificial intelligence. To perform a task, to reach conclusions from data, a computer as well as any living being needs to observe and process information of a diverse nature. For a long time now, we have been designing and inventing algorithms and systems that can solve a problem, very accurately and at incredible speed, but all algorithms are limited to the very specific task they were designed for. On the other hand, living beings in general and human beings (as well as many other animals) exhibit this incredible capacity to adapt and improve using their experience, their errors, and what they observe in the world.
Trying to understand how it is possible to learn from experience and adapt to changing conditions has always been a great topic of science. Since the invention of computers, one of the main goals has been to reproduce this type of skill in a machine.
Machine learning is the study of algorithms that can learn and adapt from data and observation, reason, and perform tasks using learned models and algorithms. As the world we live in is inherently uncertain, in the sense that even the simplest observation such as the color of the sky is impossible to determine absolutely, we needed a theory that can encompass this uncertainty. The most natural one is the theory of probability, which will serve as the mathematical foundation of the present book.
But when the amount of data grows to very large datasets, even the simplest probabilistic tasks can become cumbersome and we need a framework that will allow the easy development of models and algorithms that have the necessary complexity to deal with real-world problems.
By real-world problems, we really think of tasks that a human being is able to do such as understanding people's speech, driving a car, trading the stock exchange, recognizing people's faces on a picture, or making a medical diagnosis.
At the beginning of artificial intelligence, building such models and algorithms was a very complex task and, every time a new algorithm was invented, implemented, and programmed with inherent sources of errors and bias. The framework we present in this book, called probabilistic graphical models, aims at separating the tasks of designing a model and implementing algorithm. Because it is based on probability theory and graph theory, it has very strong mathematical foundations. But also, it is a framework where the practitioner doesn't need to write and rewrite algorithms all the time, for algorithms were designed to solve very generic problems and already exist.
Moreover, probabilistic graphical models are based on machine learning techniques which will help the practitioner to create new models from data in the easiest way.
Algorithms in probabilistic graphical models can learn new models from data and answer all sorts of questions using those data and the models, and of course adapt and improve the models when new data is available.
In this book, we will also see that probabilistic graphical models are a mathematical generalization of many standard and classical models that we all know and that we can reuse, mix, and modify within this framework.
The rest of this chapter will introduce required notions in probabilities and graph theory to help you understand and use probabilistic graphical models in R.
One last note about the title of the book: Learning Probabilistic Graphical Models in R. In fact this title has two meanings: you will learn how to make probabilistic graphical models, and you will learn how the computer can learn probabilistic graphical models. This is machine learning!
Probabilistic graphical models, seen from the point of view of mathematics, are a way to represent a probability distribution over several variables, which is called a joint probability distribution. In other words, it is a tool to represent numerical beliefs in the joint occurrence of several variables. Seen like this, it looks simple, but what PGM addresses is the representation of these kinds of probability distribution over many variables. In some cases, many could be really a lot, such as thousands to millions. In this section, we will review the basic notions that are fundamental to PGMs and see their basic implementation in R. If you're already familiar with these, you can easily skip this section. We start by asking why probabilities are a good tool to represent one's belief about facts and events, then we will explore the basics of probability calculus. Next we will introduce the fundamental building blocks of any Bayesian model and do a few simple yet interesting computations. Finally, we will speak about the main topic of this book: Bayesian inference.
Did I say Bayesian inference was the main topic before? Indeed, probabilistic graphical models are also a state-of-the-art approach to performing Bayesian inference or in other words to computing new facts and conclusions from your previous beliefs and supplying new data.
This principle of updating a probabilistic model was first discovered by Thomas Bayes and publish by his friend Richard Price in 1763 in the now famous An Essay toward solving a Problem in the Doctrine of Chances.
Probability theory is nothing but common sense reduced to calculation | ||
| --Théorie analytique des probabilités,1821. Pierre-Simon, marquis de Laplace | ||
As Pierre-Simon Laplace was saying, probabilities are a tool to quantify our common-sense reasoning and our degree of belief. It is interesting to note that, in the context of machine learning, this concept of belief has been somehow extended to the machine, that is, to the computer. Through the use of algorithms, the computer will represent its belief about certain facts and events with probabilities.
So let's take a simple example that everyone knows: the game of flipping a coin. What's the probability or the chance that coin will land on a head, or on a tail? Everyone should and will answer, with reason, a 50% chance or a probability of 0.5 (remember, probabilities are numbered between 0 and 1).
This simple notion has two interpretations. One we will call a frequentist interpretation and the other one a Bayesian interpretation. The first one, the frequentist, means that, if we flip the coin many times, in the long term it will land heads-up half of the time and tails-up the other half of the time. Using numbers, it will have a 50% chance of landing on one side, or a probability of 0.5. However, this frequentist concept, as the name suggests, is valid only if one can repeat the experiment a very large number of times. Indeed, it would not make any sense to talk about frequency if you observe a fact only once or twice. The Bayesian interpretation, on the other hand, quantifies our uncertainty about a fact or an event by assigning a number (between 0 and 1, or 0% and 100%) to it. If you flip a coin, even before playing, I'm sure you will assign a 50% chance to each face. If you watch a horse race with 10 horses and you know nothing about the horses and their rides, you will certainly assign a probability of 0.1 (or 10%) to each horse.
Flipping a coin is an experiment you can do many times, thousands of times or more if you want. However, a horse race is not an experiment you can repeat numerous times. And what is the probability your favorite team will win the next football game? It is certainly not an experiment you can do many times: in fact you will do it once, because there is only one match. But because you strongly believe your team is the best this year, you will assign a probability of, say, 0.9 that your team will win the next game.
The main advantage of the Bayesian interpretation is that it does not use the notion of long-term frequency or repetition of the same experiment.
In machine learning, probabilities are the basic components of most of the systems and algorithms. You might want to know the probability that an e-mail you received is a spam (junk) e-mail. You want to know the probability that the next customer on your online site will buy the same item as the previous customer (and whether your website should advertise it right away). You want to know the probability that, next month, your shop will have as many customers as this month.
As you can see with these examples, the line between purely frequentist and purely Bayesian is far from being clear. And the good news is that the rules of probability calculus are rigorously the same, whatever interpretation you choose (or not).
A central theme in machine learning and especially in probabilistic graphical models is the notion of a conditional probability. In fact, let's be clear, probabilistic graphical models are all about conditional probability. Let's get back to our horse race example. We say that, if you know nothing about the riders and their horses, you would assign, say, a probability of 0.1 to each (assuming there are 10 horses). Now, you just learned that the best rider in the country is participating in this race. Would you give him the same chance as the others? Certainly not! Therefore the probability for this rider to win is, say, 19% and therefore, we will say that all other riders have a probability to win of only 9%. This is a conditional probability: that is, a probability of an event based on knowing the outcome of another event. This notion of probability matches perfectly changing our minds intuitively or updating our beliefs (in more technical terms) given a new piece of information. At the same time we also saw a simple example of Bayesian update where we reconsidered and updated our beliefs given a new fact. Probabilistic graphical models are all about that but just with more complex situations.
In the previous section we saw why probabilities are a good tool to represent uncertainty or the beliefs and frequency of an event or a fact. We also mentioned the fact that the same rules of calculus apply for both the Bayesian and the frequentist interpretation. In this section, we will have a first look at the basic probability rules of calculus, and introduce the notion of a random variable which is central to Bayesian reasoning and the probabilistic graphical models.
In this section we introduce the basic concepts and the language used in probability theory that we will use throughout the book. If you already know those concepts, you can skip this section.
A sample space Ω is the set of all possible outcomes of an experiment. In this set, we call ω a point of Ω, a realization. And finally we call a subset of Ω an event.
For example, if we toss a coin once, we can have heads (H) or tails (T). We say that the sample space is  . An event could be I get a head (H). If we toss the coin twice, the sample space is bigger and we can have all those possibilities
. An event could be I get a head (H). If we toss the coin twice, the sample space is bigger and we can have all those possibilities  . An event could be I get a head first. Therefore my event is
. An event could be I get a head first. Therefore my event is  .
.
A more advanced example could be the measurement of someone's height in centimeters. The sample space is all the positive numbers from 0.0 to 10.9. Chances are that none of your friends will be 10.9 meters tall, but it does no harm to the theory. An event could be all the basketball players, that is, measurements that are 2 meters or more. In mathematical notation we write in terms of intervals  and
and  .
.
A probability is a real number Pr(E) that we assign to every event E. A probability must satisfy the three following axioms. Before writing them, it is time to recall why we're using these axioms. If you remember, we said that, whatever the interpretation of the probabilities that we make (frequentist or Bayesian), the rules governing the calculus of probability are the same:
-
For every event E,
 : we just say that probability is always positive
: we just say that probability is always positive  , which means that the probability of having any of all the possible events is always 1. Therefore, from axiom 1 and 2, any probability is always between 0 and 1.
, which means that the probability of having any of all the possible events is always 1. Therefore, from axiom 1 and 2, any probability is always between 0 and 1.
-
If you have independent events E1, E2, … then
 .
.
In a computer program, a variable is a name or a label associated to a storage space somewhere in the computer's memory. A program's variable is therefore defined by its location (and in many languages its type) and holds one and only one value. The value can be complex like an array or a data structure. The most important thing is that, at any time, the value is well known and not subject to change unless someone decides to change it. In other words, the value can only change if the algorithm using it changes it.
A random variable is something different: it is a function from a sample space into real numbers. For example, in some experiments, random variables are implicitly used:
When throwing two dices, X is the sum of the numbers is a random variable
When tossing a coin N times, X is the number of heads in N tosses is a random variable
For each possible event, we can associate a probability pi and the set of all those probabilities is the probability distribution of the random variable.
Let's see an example: we consider an experiment in which we toss a coin three times. A sample point (from the sample space) is the result of the three tosses. For example, HHT, two heads and one tail, is a sample point.
Therefore, it is easy to enumerate all the possible outcomes and find that the sample space is:

Let's Hi be the event that the ith toss is a head. So for example:

If we assign a probability of  to each sample point, then using enumeration we see that
to each sample point, then using enumeration we see that  .
.
Under this probability model, the events H1, H2, H3 are mutually independent. To verify, we first write that:

We must also check each pair. For example:

The same applies to the two other pairs. Therefore H1, H2, H3 are mutually independent. In general, we write that the probability of two independent events is the product of their probability:  . And we write that the probability of two disjoint independent events is the sum of their probability:
. And we write that the probability of two disjoint independent events is the sum of their probability: 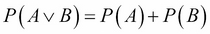 .
.
If we consider a different outcome, we can define another probability distribution. For example, let's consider again the experiment in which a coin is tossed three times. This time we consider the random variable X as the number of heads obtained after three tosses.
A complete enumeration gives the same sample space as before:

But as we consider the number of heads, the random variable X will map the sample space to the following numbers this time:
|
s |
HHH |
HHT |
HTH |
THH |
TTH |
THT |
HTT |
TTT |
|---|---|---|---|---|---|---|---|---|
|
X(s) |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
So the range for the random variable X is now {0,1,2,3}. If we assume the same probability for all points as before, that is  , then we can deduce the probability function on the range of X:
, then we can deduce the probability function on the range of X:
|
x |
0 |
1 |
2 |
3 |
|---|---|---|---|---|
|
P(X=x) |
 |
 |
 |
 |
Let's come back to the first game: 2 heads and a 6 simultaneously, the hard game with a low probability of winning. We can associate to the coin toss experiment a random variable N, which is the number of heads after two tosses. This random variable summarizes our experiment very well and N can take the values 0, 1, or 2. So instead of saying we're interested in the event of having two heads, we can say equivalently that we are interested in the event N=2. This approach allows us to look at other events, such as having only one head (HT or TH) and even having zero heads (TT). We say that the function assigning a probability to each value of N is called a probability distribution. Another random variable is D, the number we obtain when we throw a dice.
When we consider the two experiments together (tossing a coin twice and throwing a dice), we are interested in the probability of obtaining either 0, 1, or 2 heads and at the same time obtaining either 1, 2, 3, 4, 5, or 6 with the dice. The probability distribution of these two random variables considered at the same time is written P(N, D) and it is called a joint probability distribution.
If we keep adding more and more experiments and therefore more and more variables, we can write a very big and complex joint probability distribution. For example, I could be interested in the probability that it will rain tomorrow, that the stock market will rise and that there will be a traffic jam on the highway that I take to go to work. It's a complex one but not unrealistic. I'm almost sure that the stock market and the weather are really not dependent. However, the traffic condition and the weather are seriously connected. I would like to write the distribution P(W, M, T)—weather, market, traffic—but it seems to be overly complex. In fact, it is not and this is what we will see throughout this book.
A probabilistic graphical model is a joint probability distribution. And nothing else.
One last and very important notion regarding joint probability distributions is marginalization. When you have a probability distribution over several random variables, that is a joint probability distribution, you may want to eliminate some of the variables from this distribution to have a distribution on fewer variables. This operation is very important. The marginal distribution p(X) of a joint distribution p(X, Y) is obtained by the following operation:
 where we sum the probabilities over all the possible values of y. By doing so, you can eliminate Y from P(X, Y). As an exercise, I'll let you think about the link between this and the probability of two disjoint events that we saw earlier.
where we sum the probabilities over all the possible values of y. By doing so, you can eliminate Y from P(X, Y). As an exercise, I'll let you think about the link between this and the probability of two disjoint events that we saw earlier.
For the math-orientated readers, when Y is a continuous variable, the marginalization can be written as  .
.
This operation is extremely important and hard to compute for probabilistic graphical models and most if not all the algorithms for PGM try to propose an efficient solution to this problem. Thanks to these algorithms, we can do complex yet efficient models on many variables with real-world data.
Let's continue our exploration of the basic concepts we need to play with probabilistic graphical models. We saw the notion of marginalization, which is important because, when you have a complex model, you may want to extract information about one or a few variables of interest. And this is when marginalization is used.
But the two most important concepts are conditional probability and Bayes' rule.
A conditional probability is the probability of an event conditioned on the knowledge of another event. Obviously, the two events must be somehow dependent otherwise knowing one will not change anything for the other:
What's the probability of rain tomorrow? And what's the probability of a traffic jam in the streets?
Knowing it's going to rain tomorrow, what is now the probability of a traffic jam? Presumably higher than if you knew nothing.
This is a conditional probability. In more formal terms, we can write the following formula:
 and
and 
From these two equations we can easily deduce the Bayes formula:

This formula is the most important and it helps invert probabilistic relationships. This is the chef d'oeuvre of Laplace's career and one of the most important formulas in modern science. Yet it is very simple.
In this formula, we call P(X | Y) the posterior distribution of X given Y. Therefore, we also call P(X) the prior distribution. We also call P(Y | X) the likelihood and finally P(Y) is the normalization factor.
The normalization factor needs a bit of explanation and development here. Recall that  . And also, we saw that
. And also, we saw that  , an operation we called marginalization, whose goal was to eliminate (or marginalize out) a variable from a joint probability distribution.
, an operation we called marginalization, whose goal was to eliminate (or marginalize out) a variable from a joint probability distribution.
So from there, we can write  .
.
Thanks to this magic bit of simple algebra, we can rewrite the Bayes' formula in its general form and also the most convenient one:

The simple beauty of this form is that we only need to specify and use P(Y |X) and P(X), that is, the prior and likelihood. Despite the simple form, the sum in the denominator, as we will see in the rest of this book, can be a hard problem to solve and advanced techniques will be required for advanced problems.
Now that we saw the famous formula with X and Y, two random variables, let me rewrite it with two other variables. After all, the letters are not important but it can shed some light on the intuition behind this formula:

The intuition behind these concepts is the following:
The prior distribution P(θ) is what I believe about X before everything else is known—my initial belief.
The likelihood given a value for θ, what is the data D that I could generate, or in other terms what is the probability of D for all values of θ?
The posterior distribution P(θ | D) is finally the new belief I have about θ given some data D I observed.
This formula also gives the basis of a forward process to update my beliefs about the variable θ. Applying Bayes' rule will calculate the new distribution of θ. And if I receive new information again, I can update my beliefs again, and again.
In this section we will look at our first Bayesian program in R. We will define discrete random variables, that is, random variables that can only take a predefined number of values. Let's say we have a machine that makes light bulbs. You want to know if the machine works as planned or if it's broken. In order to do that you can test each bulb but that would be too many bulbs to test. With only a few samples and Bayes' rule you can estimate if the machine is correctly working or not.
When building a Bayesian model, we need to always set up the two main components:
The prior distribution
The likelihood
In this example, we won't need a specific package; we just need to write a simple function to implement a simple form of the Bayes' rule.
The prior distribution is our initial belief on how the machine is working or not. We identified a first random variable M for the state of the machine. This random variable can have two states {working, broken}. We believe our machine is working well because it's a good machine, so let's say the prior distribution is as follows:

It simply says that our belief that the machine is working is really high, with a probability of 99% and only a 1% chance that it is broken. Here, clearly we're using the Bayesian interpretation of probability because we don't have many machines but just one. We could also ask the machine's vendor about the frequency of working machines he or she is able to produce. And we could use his or her number and, in that case, this probability would have a frequentist interpretation. Nevertheless, the Bayes' rule works in all the cases.
The second random variable is L and it is the light bulb produced by the machine. The light bulb can either be good or bad. So this random variable will have two states again {good, bad}.
Again, we need to give a prior distribution for the light bulb variable L: in the Bayes' formula, it is required that we specify a prior distribution and the likelihood distribution. In this case, the likelihood is P(L | M) and not simply P(L).
Here we need in fact to define two probability distributions: one when the machine works M = working and one when the machine is broken M = broken. And we ask the question twice:
How likely is it to have a good or a bad light bulb when the machine is working?
How likely is it to have a good or a bad light bulb when the machine is not working?
Let's try to give our best guess, either Bayesian or frequentist, because we have some statistics:

Here we believe that, if the machine is working, it will only give one bad light bulb out of 100, which is even higher than what we said before. But in this case, we know that the machine is working so we expect a very high success rate. However, if the machine is broken, we say we expect at least 40% of the light bulbs to be bad. From now on, we have fully specified our model and we can start using it.
Using a Bayesian model is to compute posterior distributions when a new fact is available. In our case, we want to know if the machine is working knowing that we just observed that our latest light bulb was not working. So we want to compute P(M | L). We just specified P(M) and P(L | M), so the last thing we have to do is to use the Bayes' formula to invert the probability distribution.
For example, let's say the last produced light bulb is bad, that is, L = bad. Using the Bayes formula we obtain:


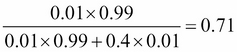
Or if you prefer, a 71% chance that the machine is working. It's lower but follows our intuition that the machine might still work. After all even if we received a bad light bulb, it's only one and maybe the next will still be good.
Let's try to redo the same problem, with equal priors on the state of the machine: a 50% chance the machine is working and 50% the machine is broken. The result is therefore:

It is a 2.4% chance the machine is working! That's very low. Indeed, given the apparent quality of this machine, as modeled in the likelihood, it appears very surprising that the machine can produce a bad light bulb. In this case, we didn't make the assumption that the machine was working as in the previous example, and having a bad light bulb can be seen as an indication that something is wrong.
After seeing this previous example, the first legitimate question one can ask is what we would do if we observed more than one light bulb. Indeed, it seems a bit strange to conclude that the machine needs to be repaired only after seeing one bad light bulb. The Bayesian way to do it is to use the posterior as the new prior and update the posterior distribution in sequence. As it would be a bit onerous to do that by hand, we will write our first Bayesian program in R.
The following code is a function that computes the posterior distribution of a random variable given the prior distribution and the likelihood and a sequence of observed data. This function takes three arguments: the prior distribution, the likelihood, and a sequence of data. The prior and data are a vector and the likelihood a matrix:
prior <- c(working = 0.99, broken = 0.01) likelihood <- rbind( working = c(good=0.99, bad=0.01), broken = c(good=0.6, bad=0.4)) data <- c("bad","bad","bad","bad")
So we defined three variables, the prior with two states working and broken, the likelihood we specified for each condition of the machine (working or broken), and the distribution over the variable L of the light bulb. So that's four values in total and the R matrix is indeed like the conditional distribution we defined in the previous section:
likelihood good bad working 0.99 0.01 broken 0.60 0.40
The data variable contains the sequence of observed light bulbs we will use to test our machine and compute the posterior probabilities. So, now we can define our Bayesian update function as follows:
bayes <- function(prior, likelihood, data) { posterior <- matrix(0, nrow=length(data), ncol=length(prior)) dimnames(posterior) <- list(data, names(prior)) initial_prior <- prior for(i in 1:length(data)) { posterior[i, ] <- prior*likelihood[ , data[i]]/ sum(prior * likelihood[ , data[i]]) prior <- posterior[i , ] } return(rbind(initial_prior,posterior)) }
This function does the following:
It creates a matrix to store the results of the successive computation of the posterior distributions
Then for each data it computes the posterior distribution given the current prior: you can see the Bayes formula in the R code, exactly as we saw it earlier
Finally, the new prior is the current posterior and the same process can be re-iterated
In the end, the function returns a matrix with the initial prior and all subsequent posterior distributions.
Let's do a few runs to understand how it works. We will use the function matplot to draw the evolution of the two distributions, one for the posterior probability that the machine is working (in green) and the other in red, meaning that the machine is broken:
matplot( bayes(prior,likelihood,data), t='b', lty=1, pch=20, col=c(3,2))
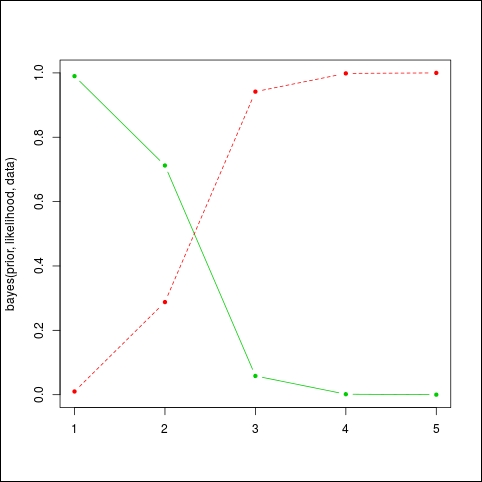
The result can be seen on the following graph: as the bad light bulbs arrive, the probability that the machine will fail quickly falls (the plain or green line). We expected something like 1 bad light bulb out of 100, and not that many. So this machine needs maintenance now. The red or dashed line represents the probability that the machine is broken.
If the prior was different, we would have seen a different evolution. For example, let's say that we have no idea if the machine is broken or not, that is, we give an equal chance to each situation:
prior <- c(working = 0.5, broken = 0.5)
Run the code again:
matplot( bayes(prior,likelihood,data), t='b', lty=1, pch=20, col=c(3,2))
Again we obtain a quick convergence to very high probabilities that the machine is broken, which is not surprising given the long sequence of bad light bulbs:

If we keep playing with the data we might see different behaviors again. For example, let's say we assume the machine is working well, with a 99% probability. And we observe a sequence of 10 light bulbs, among which the first one is bad. In R we have:
prior=c(working=0.99,broken=0.01) data=c("bad","good","good","good","good","good","good","good","good","good") matplot(bayes(prior,likelihood,data),t='b',pch=20,col=c(3,2))
And the result is given in the following graph:

The algorithm hesitates at first because, given such a good machine, it's unlikely to see a bad light bulb, but then it will converge back to high probabilities again, because the sequence of good light bulbs does not indicate any problem.
This concludes our first example of a Bayesian model with R. In the rest of this chapter, we will see how to create real-world models, with more than just two very simple random variables, and how to solve two important problems:
The problem of inference, which is the problem of computing the posterior distribution when we receive new data
The problem of learning, which is the determination of prior probabilities from a dataset
A careful reader should now ask: doesn't this little algorithm we just saw solve the problem of inference? Indeed it does, but only when one has two discrete variables, which is a bit too simple to capture the complexity of the world. We will introduce now the core of this book and the main tool for performing Bayesian inference: probabilistic graphical models.
In the last section of this chapter, we introduce probabilistic graphical models as a generic framework to build and use complex probabilistic models from simple building blocks. Such complex models are often necessary to represent the complexity of the task to solve. Complex doesn't mean complicated and often the simple things are the best and most efficient. Complex means that, in order to represent and solve tasks where we have a lot of inputs, components, or data, we need a model that is not completely trivial but reaches the necessary degree of complexity.
Such complex problems can be decomposed into simpler problems that will interact with each other. Ultimately, the most simple building block will be one variable. This variable will have a random value, or a value subject to uncertainty as we saw in the previous section.
If you remember, we saw that it is possible to represent really advanced concepts using a probability distribution; when we have many random variables, we call this distribution a joint distribution. Sometimes it is not impossible to have hundreds if not thousands or more of those random variables. Representing such a big distribution is extremely hard and in most cases impossible.
For example, in medical diagnoses, each random variable could represent a symptom. We can have dozens of them. Other random variables could represent the age of the patient, the gender of the patient, his or her temperature, blood pressure, and so on. We can use many different variables to represent the health state of a patient. We can also add other information such as recent weather conditions, the age of the patient, and his or her diet.
Then there are two tasks we want to solve with such a complex system:
From a database of patients, we want to assess and discover all the probability distributions and their associated parameters, automatically of course.
We want to put questions to the model, such as, "If I observe a series of symptoms, is my patient healthy or not?" Similarly, "If I change this or that in my patient's diet and give this drug, will my patient recover?"
However, there is something important: in such a model we would like to use another important piece of knowledge, maybe one of the most important: interactions between the various components—in other words, dependencies between the random variables. For example, there are obvious dependencies between symptoms and disease. On the other end, diet and symptoms can have a more distant dependency or can be dependent through another variable such as age or gender.
Finally, all the reasoning that is done with such a model is probabilistic in nature. From the observation of a variable X, we want to infer the posterior distribution of some other variables and have their probability rather than a simple yes or no answer. Having a probability gives us a richer answer than a binary response.
Let's make a simple computation. Imagine we have two binary random variables such as the one we saw in the previous section of this chapter. Let's call them X and Y. The joint probability distribution over these two variables is P(X,Y). They are binary so they can take two values each, which we will call x1,x2 and y1,y2, for the sake of clarity.
How many probability values do we need to specify? Four in total for P(X=x1,Y=y1), P(X=x1,Y=y2), P(X=x2,Y=y1), and P(X=x2,Y=y2).
Let's say we have now not two binary random variables, but ten. It's still a very simple model, isn't it? Let's call the variables X1,X2,X3,X4,X5,X6,X7,X8,X9,X10. In this case, we need to provide 210 = 1024 values to determine our joint probability distribution. And what if we add another 10 variables for a total of 20 variables? It's still a very small model. But we need to specify 220 = 1048576 values. This is more than a million values. So for such a simple model, the task becomes simply impossible!
Probabilistic graphical models is the right framework to describe such models in a compact way and allow their construction and use in a most efficient manner. In fact, it is not unheard of to use probabilistic graphical models with thousands of variables. Of course, the computer model doesn't store billions of values, but in fact uses conditional independence in order to make the model tractable and representable in a computer's memory. Moreover, conditional independence adds structural knowledge to the model, which can make a massive difference.
In a probabilistic graphical model, such knowledge between variables can be represented with a graph. Here is an example from the medical world: how to diagnose a cold. This is just an example and by no means medical advice. It is over-simplified for the sake of simplicity. We have several random variables such as:
Se: The season of the year
N: The nose is blocked
H: The patient has a headache
S: The patient regularly sneezes
C: The patient coughs
Cold: The patient has a cold
Because each of the symptoms can exist in different degrees, it is natural to represent the variables as random variables. For example, if the patient's nose is a bit blocked, we will assign a probability of, say, 60% to this variable, that is P(N=blocked)=0.6 and P(N=not blocked)=0.4.
In this example, the probability distribution P(Se,N,H,S,C,Cold) will require 4 * 25 = 128 values in total (4 seasons and 2 values for each other random variables). It's quite a lot and honestly it's quite hard to determine things such as the probability that the nose is not blocked and that the patient has a headache and sneezes and so on.
However, we can say that a headache is not directly related to a cough or a blocked nose, except when the patient has a cold. Indeed, the patient could have a headache for many other reasons.
Moreover, we can say that the Season has quite a direct effect on Sneezing, Blocked Nose, or Cough but less or none on Headache. In a probabilistic graphical model, we will represent these dependency relationships with a graph, as follows, where each random variable is a node in the graph and each relationship is an arrow between two nodes:

As you can see in the preceding figure, there is a direct relationship between each node and each variable of the probabilistic graphical model and also a direct relationship between arrows and the way we can simplify the joint probability distribution in order to make it tractable.
Using a graph as a model to simplify a complex (and sometimes complicated) distribution presents numerous benefits:
First of all, as we observed in the previous example, and in general when we model a problem, random variables interact directly with only small subsets of other random variables. Therefore, this promotes a more compact and tractable model.
Knowledge and dependencies represented in a graph are easy to understand and communicate.
The graph induces a compact representation of the joint probability distribution and is easy to make computations with.
Algorithms to perform inference and learning can use graph theory and the associated algorithms to improve and facilitate all the inference and learning algorithms: compared to the raw joint probability distribution, using a PGM will speed up computations by several orders of magnitude.
In the previous example on the diagnosis of the common cold, we defined a simple model with a few variables Se, N, H, S, C, and R. We saw that, for such a simple expert system, we needed 128 parameters!
We also saw that we can make a few independence assumptions based only on common sense or common knowledge. Later in this book, we will see how to discover those assumptions from a data set (also called structural learning).
So we can rewrite our joint probability distribution taking into account these assumptions as follows:

In this distribution, we did a factorization; that is, we expressed the original joint distribution as a product of factors. In this case, the factors are simpler probability distributions such as P(C | Cold), the probability of coughing given that one has a cold. And as we considered all the variables to be binary (except Season, which can take of course four values), each small factor (distribution) will need only a few parameters to be determined: 4 + 23 + 23 + 2 +22 + 22 =30. Only 30 easy parameters instead of 128! It's a massive improvement.
I said the parameters are easy, because they're easy to determine, either by hand or from data. For example, we don't know if the patient has a cold or not, so we can assign equal probability to the variable Cold, that is P(Cold = true)=P(Cold = false)=0.5.
Similarly, it's easy to determine P(C | Cold) because, if the patient has a cold (Cold=true), he or she will likely cough. If he or she has no cold, then chances will be low for the patient to cough, but not zero because the cause could be something else.
In general, a directed probabilistic graphical model factorizes a joint distribution over the random variables X1, X2…Xn as follows:

pa(Xi) is the subset of parent variables of the variable Xi as defined in the graph.
The parents are easy to read on a graph: when an arrow goes from A to B, then A is the parent of B. A node can have as many children as needed and a node can have as many parents as needed too.
Directed models are good for representing problems in which causality has to be modeled. It is also a good model for learning from parameters because each local probability distribution is easy to learn.
Several times in this chapter, we mentioned the fact that PGM can be built using simple blocks and assembled to make a bigger model. In the case of directed models, the blocks are the small probability distributions P(Xi | pa(Xi)).
Moreover, if one wants to extend the model by defining new variables and relations, it is as simple as extending the graph. The algorithms designed for directed PGM work for any graph, whatever its size.
Nevertheless, not all probability distributions can be represented by a directed PGM and sometimes it is necessary to relax certain assumptions.
Also it is important to note the graph must be acyclic. It means that you can't have an arrow from node A to node B and from node B to node A as in the following figure:

In fact, this graph does not represent a factorization at all as defined earlier and it would mean something like A is a cause of B while at the same time B is a cause of A. It's paradoxical and has no equivalent mathematical formula.
When the assumption or relationships are not directed, there exists a second form of probabilistic graphical model in which all the edges are undirected. It is called an undirected probabilistic graphical model or a Markov network.
An undirected probabilistic graphical model factorizes a joint distribution over the random variables X1, X2…Xn as follows:

This formula needs a bit of explanation:
The first term on the left-hand side is our now usual joint probability distribution
The constant Z is a normalization constant, ensuring that the right-hand term will sum to 1, because it's a probability distribution
φc is a factor over a subset of variables χc such that each member of this subset is a maximal clique, that is a sub-graph in which all the nodes are connected together:

In the preceding figure, we have four nodes and the φc functions will be defined on the subsets that are maximal cliques—that is {ABC} and {A,D}. So the distribution is not very complex after all. This type of model is used a lot in applications such as computer vision, image processing, finance, and many more applications where the relationships between the variables follow a regular pattern.
It's about time to talk about the applications of probabilistic graphical models. There are so many applications that I would need another hundred pages to describe a subset of them. As we saw, it is a very powerful framework to model complex probabilistic models by making them easy to interpret and tractable.
In this section, we will use our two previous models: the light bulb machine and the cold diagnosis.
We recall that the cold diagnosis model has the following factorization:

The light bulb machine, though, is defined by two variables only: L and M. And the factorization is very simple:

The graph corresponding to this distribution is simply:

In order to represent our probabilistic graphical model, we will use an R package called gRain. To install it:
source("http://bioconductor.org/biocLite.R") biocLite() install.packages("gRain")
Note that the installation can take several minutes because this package depends on many other packages (and especially one we will use often called gRbase) and provides the base functions for manipulating graphs.
When the package is installed, you can load the base package with:
library("gRbase")
First of all, we want to define a simple undirected graph with five variables A, B, C, D and E:
graph <- ug("A:B:E + C:E:D") class(graph)
We define a graph with a clique between A, B, and E, and another clique between C, E, and D. This will form a butterfly graph. The syntax is very simple: in the string each clique is separated by a + and each clique is defined by the name of each variable separated by a colon.
Next we need to install a graph visualization library. We will use the popular Rgraphviz and to install it you can enter:
install.packages("Rgraphviz") plot(graph)
You will obtain your first undirected graph as follows:

Next we want to define a directed graph. Let's say we have again the same {A,B,C,D,E} variables:
dag <- dag("A + B:A + C:B + D:B + E:C:D") dag plot(dag)
The syntax is again very simple: a node without parent comes alone such as A; otherwise parents are specified by the list of nodes separated by colons.
In this library, several syntaxes are available to define graphs, and you can also build them node by node. Throughout the book we will use several notations as well as a very important representation: the matrix notation. Indeed, a graph can be equivalently represented by a squared matrix where each row and each column represents a node and the coefficient in the matrix will be 1 is there is an edge; 0 otherwise. If the graph is undirected, the matrix will be symmetric; otherwise, the matrix can be anything.
Finally, with this second test we obtain the following graph:

Now we want to define a simple graph for the light bulb machine and provide numerical probabilities. Then we will do our computations again and check that the results are the same.
First we define the values for each node:
machine_val <- c("working","broken") light_bulb_val <- c("good","bad")
Then we define the numerical values as percentages for the two random variables:
machine_prob <- c(99,1) light_bulb_prob <- c(99,1,60,40)
The next step is to define the random variables with gRain:
M <- cptable(~machine, values=machine_prob, levels=machine_val) L <- cptable(~light_bulb|machine, values=light_bulb_prob, levels=light_bulb_val)
Here, cptable means conditional probability table: it's a term to designate the memory representation of a probability distribution in the case of a discrete random variable. We will come back to this notion in Chapter 2, Exact Inference.
Finally, we can compile the new graphical model before using it. Again, this notion will make more sense in Chapter 2, Exact Inference. when we look at inference algorithms such as the Junction Tree Algorithm:
plist <- compileCPT(list(M,L)) plist
When printing the network, the result should be as follows:
CPTspec with probabilities: P( machine ) P( light_bulb | machine )
Here, you clearly recognize the probability distributions that we defined earlier in this chapter.
If we print the variables' distribution we will find again what we had before:
plist$machine plist$light_bulb
This will output the following result:
> plist$machine machine working broken 0.99 0.01 > plist$light_bulb machine light_bulb working broken good 0.99 0.6 bad 0.01 0.4
And now we ask the model the posterior probability. The first step is to enter an evidence into the model (that is to say that we observed a bad light bulb) by doing as follows:
net <- grain(plist) net2 <- setEvidence(net, evidence=list(light_bulb="bad")) querygrain(net2, nodes=c("machine"))
The library will compute the result by applying its inference algorithm and will output the following result:
$machine machine working broken 0.7122302 0.2877698
And this result is rigorously the same as we obtained with the Bayes method we defined earlier.
Therefore we are now ready to create more powerful models and explore the different algorithms suitable for solving different problems. This is what we're going to learn in the next chapter on exact inference in graphical models.
In this first chapter we learned the base concepts of probabilities
We saw how and why they are used to represent uncertainty about data and knowledge, while also introducing the Bayes formula. This is the most important formula to compute posterior probabilities—that is, to update our beliefs and knowledge about a fact when new data is available
We saw what a joint probability distribution is and learnt that they can quickly become too complex and intractable to deal with. We learned the basics of probabilistic graphical models as a generic framework to perform tractable, efficient, and easy modeling with probabilistic models. Finally, we introduced the different types of probabilistic graphical model and learned how to use R packages to write our first models
In the next chapter, we will learn the first set of algorithms to do Bayesian inference with probabilistic graphical models—that is, to put questions and queries to our models. We will introduce new features of the R packages and, at the same time, we'll learn how these algorithms work and can be used in an efficient manner.




















 Download code from GitHub
Download code from GitHub

