Setting Up R and QGIS Environments for Geospatial Tasks
This chapter will walk its readers through the different stages of setting up the R and QGIS environments. R and QGIS are both free and open source software that can be used for various geospatial tasks. R benefits from more than 10,000 packages developed by its community, and QGIS also benefits from a number of plugins that are available to QGIS users. QGIS can complement R, and vice versa, for the conduct of many sophisticated geospatial tasks, and many statistical and machine learning algorithms can be very easily applied using R with the help of QGIS.
The first segment of the book starts by discussing how to install R and getting to know its environment. That is followed by data types in R, and different operations in R, and then getting acquainted with writing functions and plotting. The second segment consists of installing QGIS, learning the QGIS environment, and getting help in QGIS.
The following topics are to be covered in this chapter:
- Installing R
- Basic data types and the data structure in R
- Looping, functions, and apply family in R
- Plotting in R
- Installing QGIS
- Getting to know the QGIS environment.
Installing R
R is an open source programming language and software used for statistical computing and graphics, which has benefited greatly from the continuous contributions of its user community. Graphics in R are of very high quality, and, although it was not primarily developed for GIS purposes, with the development of packages such as ggmap, tmap, sf, raster, sp, and so on, R can work as a GIS environment itself. Furthermore, R codes can be written inside QGIS and we can also work on QGIS inside R using the RQGIS package.
We will now install R with the help of snapshots of each of the step-by-step instructions provided. The following steps have been implemented in Microsoft Windows and should also be applicable to Mac or other platforms with a little tweaking. There are no specific requirements for computer configuration, but any modern desktop or laptop will be sufficient to run the examples provided in this book.
Download R software from the following site and click on download R: https://www.r-project.org/.
Now we need to select a CRAN mirror; we will use the first link to download R.
Now we will need to click on Download R for Windows:

Click install R for the first time, as we can see from the following screenshot:

Now we just need to double-click the .exe file that we have downloaded and continue to click to accept all the defaults to complete the download of R. After we have installed R, we need to open it, and it will look similar to the following screenshot. For this installation process, a 64-bit computer is being used, but if you are using a 32-bit computer, your R windows will reflect that:
We are finally ready to rock and roll using R. But before that, we need a little bit more familiarity with R, or perhaps we need a refresher.
Basic data types and data structures in R
Before we start delving deep into R for geospatial analysis, we need to have a good understanding of how R handles and stores different types of data. We also need to know how to undertake different operations on that data.
Basic data types in R
There are three main data types in R, and they are as follows:
- Numerics
- Logical or Boolean
- Character
Numerics are any numbers with decimal values; thus, 21.0 and 21.1 are both numerics. We can use addition, subtraction, multiplication, division, and so on, with these numerics. Interestingly, R also considers integer numbers to be numerics. Logical or Boolean data consists of TRUE and FALSE; they are mainly used for different comparisons. The character variable consists of text, such as the name of something. We write character values in R by putting our character values inside "", or double quotes.
Variable
Just before digging any deeper, we need to know how to assign values to any variable. So, what is a variable? It's like a container, which holds different value(s) of different types (or the same type). When assigning multiple values to any variable, we write the variable name to the left, followed by an <- or = and then the value. So, if we want to assign 2 to a variable x, we can write either of the two:
x <- 2
or
x = 2
Data structures in R
The data structures in R are as follows:
- Vectors
- Matrices
- Arrays
- Data frames
- Lists
- Factors
Vectors
Vectors are used to store single or multiple values of similar data types in a variable and are considered to be one-dimensional arrays. That means that the x variable we just defined is a vector. If we want to create a vector with multiple numeric values, we assign as before with one additional rule: we put all the values inside c() and separate all the values with , except the last value. Let's look at an example:
val = c(1, 2, 3, 4, 5, 6)
What happens if we mix different data types such as both numerics and characters? It works! (A variable's name is arbitrarily named as val, but you can name your variable anything that you feel appropriate, anything!) Except in some cases, such as variable names, shouldn't start with any special character:
x = c(1, 2.0, 3.0, 4, 5, "Hello", "OK")
What we have just learned about storing data of the same types doesn't seem to be true then, right? Well, not exactly. What R does behind the scenes is that it tries to convert all the values mentioned for the x variable to the same type. As it can't convert Hello and OK to numeric types, for conformity it converts all the numeric values 1, 2.0, 3.0, 4, and 5 to character values: that is, "1", "2.0", "3.0", "4", and "5", and adds two more values, "Hello" and "OK", and assigns all these character values to x. We can check the class (data type) of a variable in R with class(variable_name), and let's confirm that x is indeed a character variable:
class(x)
We will see that the R window will show the following output:
[1] "character"
We can also label vectors or give names to different values according to our need. Suppose we want to assign temperature values recorded at different times to a variable with a recorded time as a label. We can do so using this code:
temperature = c(morning = 20, before_noon = 23, after_noon = 25, evening = 22, night = 18)
Basic operations with vector
Suppose the prices of three commodities, namely potatoes, rice, and oil were $10, $20, and $30 respectively in January 2018, denoted by the vector jan_price, and the prices of all these three elements increased by $1, $2, and $3 respectively in March 2018, denoted by the vector increase. Then, we can add two vectors mar_price and increase to get the new price as follows:
jan_price = c(10, 20, 30)
increase = c(1, 2, 3)
mar_price = jan_price + increase
To see the contents of mar_price, we just need to write it and then press Enter:
mar_price
We now see that mar_price is updated as expected:
[1] 11 22 33
Similarly, we can subtract and multiply. Remember that R uses element-wise computation, meaning that if we multiply two vectors which are of the same size, the first element of the first vector will be multiplied by the first element of the second vector, and the second element of the second vector will be multiplied by the second element of the second vector, and as such:
x = c(10, 20, 30)
y = c(1, 2, 3)x * y
The result of this multiplication is this:
[1] 10 40 90
If we multiply a vector with multiple values by a single value, that latter value multiplies every single element of the vector separately. This is demonstrated in the following example:
x * 2
We can see the output of the preceding command as follows:
[1] 20 40 60
As a vector does element-wise computation, if we check for any condition, the condition will be checked for each element. Thus, if we want to know which values in x are greater than 15:
x > 15
As the second and third elements satisfy this condition of being greater than 15, we see TRUE for these positions and FALSE for the first position as follows:
[1] FALSE TRUE TRUE
Indexing in R or the first element of any data type starts with 1; thus, the third or fourth element in R can be accessed with index 3 or 4. We need to access any particular index of a variable with a variable name followed by the index inside []. Thus, the third element of x can be accessed as follows:
x[3]
By pressing Enter after x[3], we see that the third element of x is this:
30
If we want to select all items but the third one, we need to use - in the following way:
x[-3]
We now see that x has all of the elements except the third one:
[1] 10 20
Matrix
Suppose, we also have the prices of these three items for the month of June as follows:
june_price = c(20, 25, 33)
Now if we want to stack all these three months in a single variable, we can't use vectors anymore; we need a new data structure. One of the data structures to rescue in this case is the matrix. A matrix is basically a two-dimensional array of data elements with a number of rows and columns fixed. Like a vector, a matrix can also contain just one type of element; a mix of two types is not allowed. To combine these three vectors with every row corresponding to a particular month's prices of different items and every column corresponding to prices of different items in a particular month, what we can do is first combine these three vectors inside a matrix() command, followed by a comma and nrow = 3, indicating the fact that there are three different items (for example, items are arranged row-wise and months are arranged column-wise).
all_prices = matrix(c(jan_price, mar_price, june_price), nrow= 3)
all_prices
The all_prices data frame will look like the following:
[,1] [,2] [,3]
[1,] 10 11 20
[2,] 20 22 25
[3,] 30 33 33
Now suppose we change our mind and want to arrange this with the items displayed column-wise and the prices displayed row-wise; that is, the first row corresponds to the prices of different items in a particular month and the first column corresponds to the first month's (January's) prices of different items, with that arrangement continuing for every other row and column. We can do so very easily by mentioning byrow = TRUE inside the matrix. byrow = TRUE arranges the values of vectors row-wise. It arranges the matrix by aligning all the elements row-wise allowing for its dimensions:
all_prices2 = matrix(c(jan_price, mar_price, june_price), nrow= 3, byrow = TRUE)
all_prices2
The output will look like the following:
[,1] [,2] [,3]
[1,] 10 20 30
[2,] 11 22 33
[3,] 20 25 33
We can see that here jan_price is considered as the first row, mar_price as the second row, and june_price as the third row in all_prices2.
Array
Arrays are also like matrices, but they allow us to have more than two dimensions. The all_prices2 row has prices of different items for January, March, and June 2018. Now, suppose we also want to record prices for 2017. We can do so by using array() and in this case we want to add two 3x3 matrices where the first one corresponds to 2018 and the latter matrix corresponds to 2017. In array(m, n, p), m and n stand for the dimensions of the matrix and p stands for how many matrices we want to store.
In the following example, we define six vectors for three different months for two different years. Now we create an array by combining six different vectors using c() and by using them inside array() as inputs as follows:
# Create six vectors
jan_2018 = c(10, 11, 20)
mar_2018 = c(20, 22, 25)
june_2018 = c(30, 33, 33)
jan_2017 = c(10, 10, 17)
mar_2017 = c(18, 23, 21)
june_2017 = c(25, 31, 35)
# Now combine these vectors into array
combined = array(c(jan_2018, mar_2018, june_2018, jan_2017, mar_2017, june_2017),dim = c(3,3,2))
combined
We can now see that we have two matrices of 3 x 3 dimensions, as in the output as follows:

Data frames
Data frames are like matrices, except for the one additional advantage that we can now have a mix of different element types in a data frame. For example, we can now store both numeric and character elements in this data structure. Now, we can also put the names of different food items along with their prices in different months to be stored in a data frame. First, define a variable with the names of different food items:
items = c("potato", "rice", "oil")
We can define a data frame using data.frame as follows:
all_prices3 = data.frame(items, jan_price, mar_price, june_price)
all_prices3
The data frame all_prices3 looks like the following:

Accessing elements in a data frame can be done by using either [[]] or $. To select all the values of mar_price or the second column, we can do either of the two methods provided as follows:
all_prices3$mar_price
This gives the values of the mar_price column of the all_prices3 data frame:
[1] 11 22 33
Similarly, there is the following:
all_prices3[["mar_price"]]
We now find the same output as we found by using the $ sign:
[1] 11 22 33
We can also use [] to access a data frame. In this case, we can utilize both the row and column dimensions to access an element (or elements) using the row index indicated by the number before, and the column index indicated by the number after. For example, if we wanted to access the second row and third column of all_prices3, we would write this:
all_prices3[2, 3]
This gives the following output:
[1] 22
Here, for simplicity, we will drop items column from all_prices3 using - and rename the new variable as all_prices4 and we can define this value in a new vector pen as follows:
all_prices4 = all_prices3[-1]
all_prices4
We can now see that the items column is dropped from the all_prices4 data frame:

We can add a row using rbind(). Now we define a new numerical vector that contains the price of the pen vector for January, March, and June, and we can add this row using rbind():
pen = c(3, 4, 3.5)
all_prices4 = rbind(all_prices4, pen)
all_prices4
Now we see from the following output that a new observation is added as a new row:

We can add a column using cbind(). Now, suppose we also have information on the prices of potato, rice, oil, and pen for August as given in the vector aug_price:
aug_price = c(22, 24, 31, 5)
We can now use cbind() to add aug_price as a new column to all_prices4:
all_prices4 = cbind(all_prices4, aug_price)
all_prices4
Now all_prices4 has a new column aug_price added to it:

Lists
Now, items jan_price and mar_price have four elements, whereas june_price has three elements. So, we can't use a data frame in this case to store all of these values in a single variable. Instead, we can use lists. Using lists, we can get almost all the advantages of a data frame in addition to its capacity for storing different sets of elements (columns in the case of data frames) with different lengths:
all_prices_list2 = list(items, jan_price, mar_price, june_price)
all_prices_list2
We can now see that all_prices_list2 has a different structure than that of a data frame:

Accessing list elements can be done by either using [] or [[]] where the former gives back a list and the latter gives back element(s) in its original data type. We can get the values of jan_price in the following way:
all_prices_list2[2]
Using [], we are returned with the second element of all_prices_list2 as a list again:

Note that, by using [], what we get back is another list and we can't use different mathematical operations on it directly.
class(all_prices_list2[2])
We can see, as follows, that the class of all_prices_list2 is a list:

We can get this data in original data types (that is, a numeric vector) by using [[]] instead of []:
all_prices_list2[[2]]
Now, we get the second element of the list as a vector:

We can see that it is numeric and we can check further to confirm that it is numeric:
class(all_prices_list2[[2]])
The following result confirms that it is indeed a numeric vector:

We can also create categorical variables with factor().
Suppose we have a numeric vector x and we want to convert it to a factor, we can do so by following the code as shown as follows:
x = c(1, 2, 3)
x = factor(x)
class(x)
Factor
We now see that the class is a factor, as we can see in the following output:
[1] "factor"
Now, we can also look at the internal structure of this vector x, using str() as follows:
str(x)
We now see that it converts 1, 2, and 3 to factors:
[1] Factor w/ 3 levels "1", "2", "3": 1 2 3
Looping, functions, and apply family in R
Looping allows us to do repetitive task in a couple of lines of code, saving us much effort and time. Functions allow us to write a block of instructions that could be modified to work according to the way they are being called. Combining the power of looping, functions, and apply family in R allows us to loop through the elements of a data type, or similar, and apply a function or use a block of instructions on each of these.
Looping in R
Suppose we want to loop through all the values of the aug_price column inside all_prices4 and square them and return them. We can do so in the following way:
jan = all_prices4$jan_price
for(price in jan){
print(price^2)
}
This prints a square of all the prices in January as follows:

Functions in R
We can also achieve the previous result by using a function. Let's name this function square:
square = function(data){
for(price in data){
print(price^2)
}
}
Now call the function as follows:
square(all_prices4$jan_price)
The following output also shows the squared price of jan_price:

Now suppose we want to have the ability to take elements to any power, not just square. We can attain it by making a little tweak to the function:
power_function = function(data, power){
for(price in data){
print(price^power)
}
}
Now suppose we want to take the power of 4 for the price in June, we can do the following:
power_function(all_prices4$june_price, 4)
We can see that the june_price column is taken to the fourth power as follows:

Apply family – lapply, sapply, apply, tapply
We discuss apply family here, which allows us not to have to write loops and reduces our workload. We will discuss four functions under this family: apply, lapply, sapply, and tapply.
apply
apply works on arrays or matrices and gives us an easier way to compute something row-wise or column-wise. For the apply() function, this row- or column-wise consideration is denoted by a margin. The apply() function takes the following form: apply(data, margin, function). This data has to be an array or a matrix, and the margin can be either 1 or 2, where 1 stands for a row-wise operation and 2 stands for a column-wise operation. We will work with the matrix all_prices, which has the following structure:

Here, we have a record of prices of three different items in three different months (January, March, and June), where a row represents the prices of an item in three different months and a column represents the prices of three different items in any single month. Now, if we want to know which item's price fluctuated most over these three months, we would have to compute a standard deviation row-wise for each row. We can do this very easily using margin = 1 in apply().
apply(all_prices, 1, sd)
We can see the standard deviation for these three items as follows:

Now suppose we want to know the month-wise total cost of all three items. As every column corresponds to different months, we can apply apply() with margin = 2 and a function mean to achieve this:
apply(all_prices, 2, sum)
This gives the sum for all three months in a vector:

We see that the total prices were the highest in June (the third column), totaling 78.
lapply
In the previously mentioned power_function() function, we had to use a for loop to loop through all the values of the june_price column of the all_prices4 data frame. lapply allows us to define a function (or use an already existing function) over all the elements of a list or vector and it returns a list. Let's redefine power_function() to allow for the computation of different powers on elements and then use lapply to loop through each element of a list or vector and take the power of each of these elements on every iteration of the loop. lapply() has the following format:
lapply(data, function, arguments_of_the_function)
power_function2 = function(data, power){
data^power
}
lapply(all_prices4$june_price, power_function2, 4)
As we saw in the last output, all the prices of june_price are taken to the fourth power and are returned as a list:

unlist(lapply(all_prices4$june_price, power_function2, 4))
Now we are returned the fourth power of the june_price column as a vector.

Now we will again work with a combined array, which has the prices of different items in three different months each for 2017 and 2018. Do you remember the structure of it? It looked like this:

Here, the first matrix corresponds to prices for 2017 and the second matrix corresponds to 2018. We will now recreate this array to become a list of matrices in the following way:
combined2 = list(matrix(c(jan_2018, mar_2018, june_2018), nrow = 3),
matrix(c(jan_2017, mar_2017, june_2017), nrow = 3))
combined2
This returns us the following list of matrices:

Now, if we want the prices for March for both 2017 and 2018, we can use lapply() in the following way:
lapply(combined2, "[", 2,)

So, what this has done is selected the second row from each list:

Now we can modify it further to select a column, row, or any element according to our needs.
sapply
What we have got by using unlist(lapply(data, function, arguments_of_the_function)) can be obtained simply by using sapply(data, function, arguments_of_the_function).
sapply(all_prices4$june_price, power_function2, 4)
We are returned with a vector again as follows:

Now let's go back to the example of the all_prices3 data frame. We can see this from the screenshot that follows:

tapply
Now, suppose instead of prices for 2018 only, we have prices for these items for 2017, 2016, and 2015 as well. This new data frame is defined as follows:
all_prices = data.frame(items = rep(c("potato", "rice", "oil"), 4),
jan_price = c(10, 20, 30, 10, 18, 25, 9, 17, 24, 9, 19,27),
mar_price = c(11, 22, 33, 13, 25, 32, 12, 21, 33, 15, 27,39),
june_price = c(20, 25, 33, 21, 24, 40, 17, 22, 27, 13, 18,23)
)
all_prices
The output for the preceding lines of code can be seen as follows:

Now suppose we want to take the mean price of different items for very March in all years. We can do this by using tapply(numerical_variable, categorical_variable, function). So, we will need to convert the items column of the all_prices data frame to a categorical variable to take the mean price.
tapply(all_prices$mar_price, factor(all_prices$items), mean)
This gives us a mean March price for oil, potato, and rice in all years, as follows:

Note the use of factor() to convert the items column to a factor variable.
There are other apply functions, but that's it for now, folks. We will introduce new functions as and when it will be necessary as we proceed to new chapters for geospatial analysis.
To install a new package, we need to write install.packages("package_name"), and to use any package, we need to write load.packages("package_name").
Plotting in R
We can make a simple plot using the plot() function of R. Now we will simulate 50 values from a normal distribution using rnorm() and assign these to x and similarly generate and assign 50 normally distributed values to y. We can plot these values in the following way:
x = rnorm(50)
y = rnorm(50)
# pch = 19 stands for filled dot
plot(x, y, pch = 19, col = 'blue')
This gives us the following scatterplot with blue-colored filled dots as symbols for each data point:
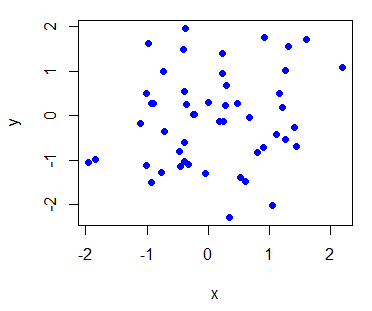
We can also generate a line plot type of graph by using type = "l" inside plot().
Now we will briefly look at a very strong graphical library called ggplot2 developed by Hadley Wickham. Remember, the all_prices data frame? If you don't, let's have another look at that:
str(all_prices)
We see that it has 12 rows and four columns, it has three numeric variables and one factor variable:

We first need to install and then load the ggplot2 package:
install.packages("ggplot2")
library(ggplot2)
Now we need to define the data frame we want to use inside the ggplot() command, and inside this command, after the data frame name, we need to write aes(), which stands for aesthetics. Inside this aes(), we define the x axis variable and the y axis variable. So, if we want to plot the prices of different items in January against these items, we can do the following:
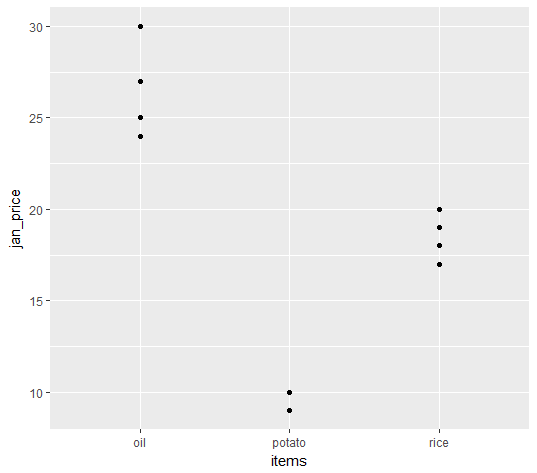
ggplot(all_prices, aes(x = items, y = jan_price)) +
geom_point()
Now we see the plot as follows:
We can also compute and mark the mean price in January of these different items over all the years under consideration using stat = "summary" and fun.y = "mean". We will just need to add another layer, geom_point(), and mention these arguments inside this:
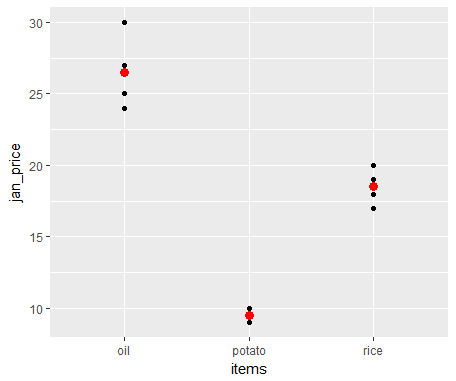
ggplot(all_prices, aes(x = items, y = jan_price)) +
geom_point() +
geom_point(stat = "summary", fun.y = "mean", colour = "red", size = 3)
The following screenshot shows that along with data points, the mean values for each item are marked as red:
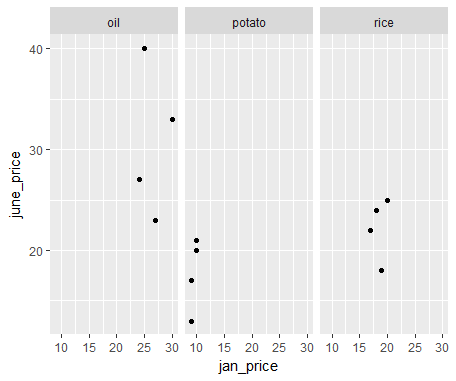
We can also plot the price of January against the price of June and make separate plots for each of the items using facet_grid(. ~ items):
ggplot(all_prices, aes(x = jan_price, y = june_price)) +
geom_point() +
facet_grid(. ~ items)
As a result, we see a scatterplot for three different items as follows:
We can also add a linear model fit using a stat_smooth() layer:
ggplot(all_prices, aes(x = jan_price, y = june_price)) +
geom_point() +
facet_grid(. ~ items) +
# se = TRUE inside stat_smooth() shows confidence interval
stat_smooth(method = "lm", se = TRUE, col = "red")
The preceding code gives a linear model fit and a 95% confidence interval along with the scatterplot:
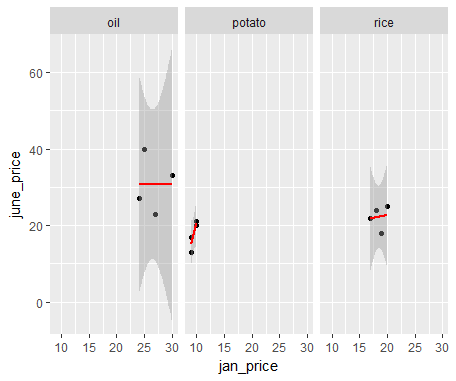
We get this weird-looking confidence interval for the oil price and the rice price, as there are very few points available.
We can do so many more things, and we have so many other things to cover in this book that we will not be covering any more plotting functionalities here. But we will explain many other aspects of plotting as and when appropriate when dealing with spatial data in upcoming chapters. I have also listed books to refer to for a deeper understanding of R in the Further reading section.
Installing QGIS
QGIS is a free and open source geographic information system (GIS) that we can use for various spatial data management and analysis tasks for different fields, such as geography, environmental science, disaster management, urban planning, climate science, and many other fields that use spatial data. The strength of QGIS lies in the fact that it is an open source platform coupled with different plugins available for computing different tasks.
QGIS can be installed in different operating systems such as Windows, Mac, Linux, Android, and so on. QGIS can be installed from the following site:
http://download.osgeo.org/qgis/win64/
After going to the previously mentioned website, we will scroll down and click on QGIS-OSGeo4W-3.2.2-1-Setup-x86_64.exe to download QGIS 3.2.2-1 (or click on the installer relevant to the operating system you are using):

Getting to know the QGIS environment
The QGIS desktop is used to display, analyze, and to do different design formatting with data. The QGIS desktop has four main components: a Menu bar, Tool Bars, Panels, and Map Display. The Menu bar is the top section and appears as follows:

Just under this, we have Tool Bars, which look like this:

We then have the Panels section on the left side, which is composed of these parts: Browser and Layers. The Browser gives us different options for data connection and working with layers. Layers shows all the vector and raster files that we can load to QGIS:
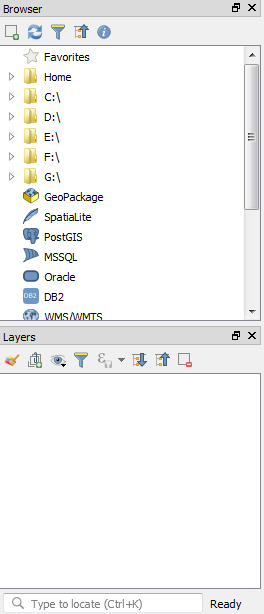
We also have Map Display, which shows us the map outputs:

In the Map Display section, as shown in the preceding screenshot, we see some of the projects the author has been working on; in your case, if you are starting afresh, this section will be blank at first.
Using QGIS, we can complete many geospatial data management and spatial data analysis tasks. The following is a screenshot of some of the useful sections of QGIS:
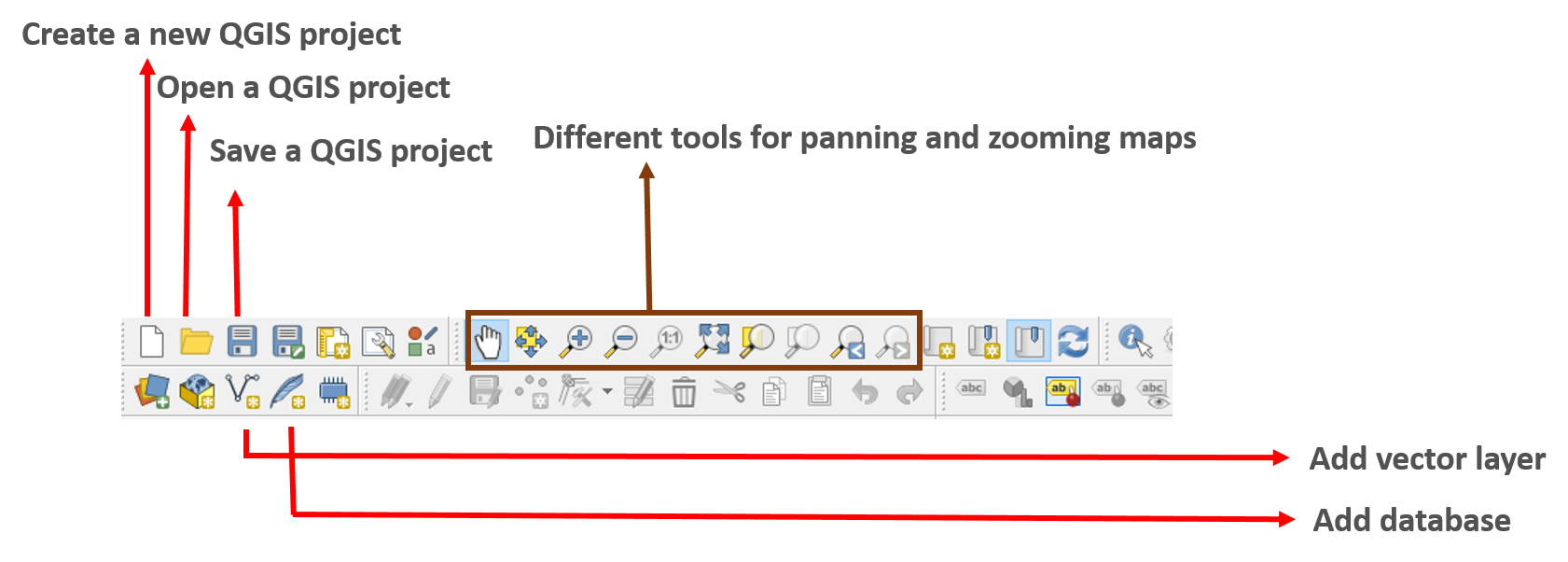
We can add different spatial data such as vector layers, raster layers, and also database layers using the different functionalities provided in QGIS: Layer | Add Layer | ...:
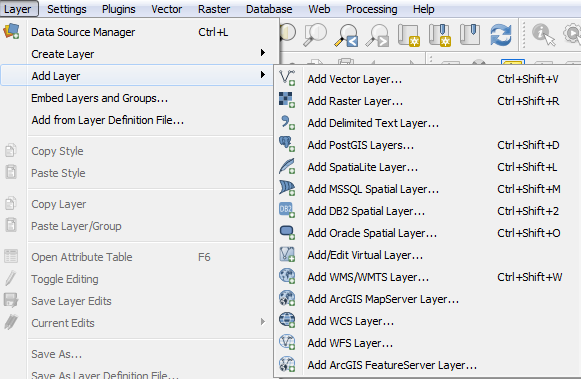
We will now add a vector file (shapefile) in QGIS to illustrate how it is being done in this GIS software. Suppose we want to add the file BGD_adm3.shp to our QGIS environment; we can do this by following these steps:
- Click on Add Vector Layer… under Add Layer, which is under Layer:

- We click on the indicated rectangular shape to browse to the folder where the shapefile we want to add is located (in the Data folder under Chapter 1):
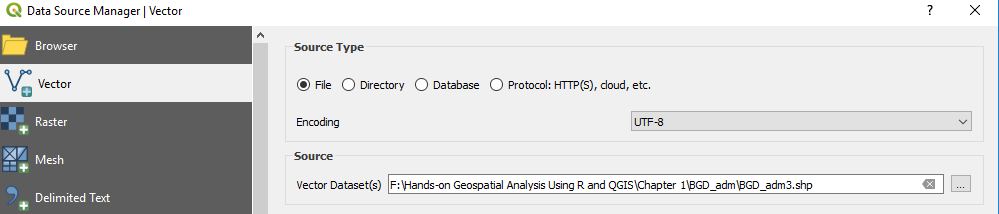
- Now we browse to BGD_adm3.shp under the Data folder of Chapter 1, select it, and then press Close:

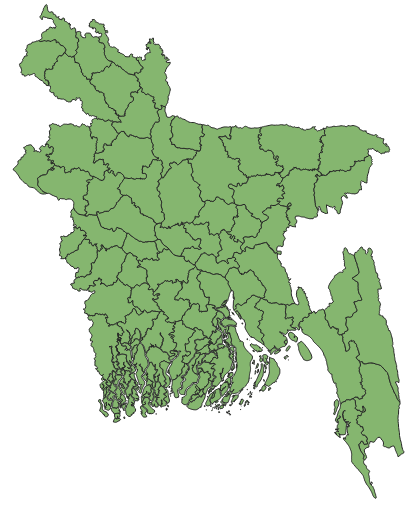
- Now click Add and then click Close. Now, we will see a map of the districts of Bangladesh in the Map Display as follows:
Now we will look at one more important aspect of vector data: its attribute table. An attribute table contains information about the shape of points, lines, and polygon features, or mainly the geometry of features, in addition to any other information associated with those features. This information is recorded in a tabular form, where each row represents a record and each column corresponds to field or a feature. We can access this table by right-clicking on the BGD_adm3 layer in the Layers panel of QGIS and then by left-clicking on Open Attribute Table:
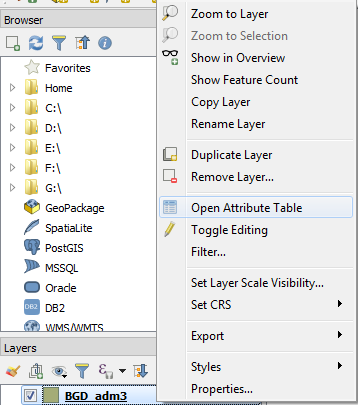
Now we will see the attribute table associated with this shapefile:
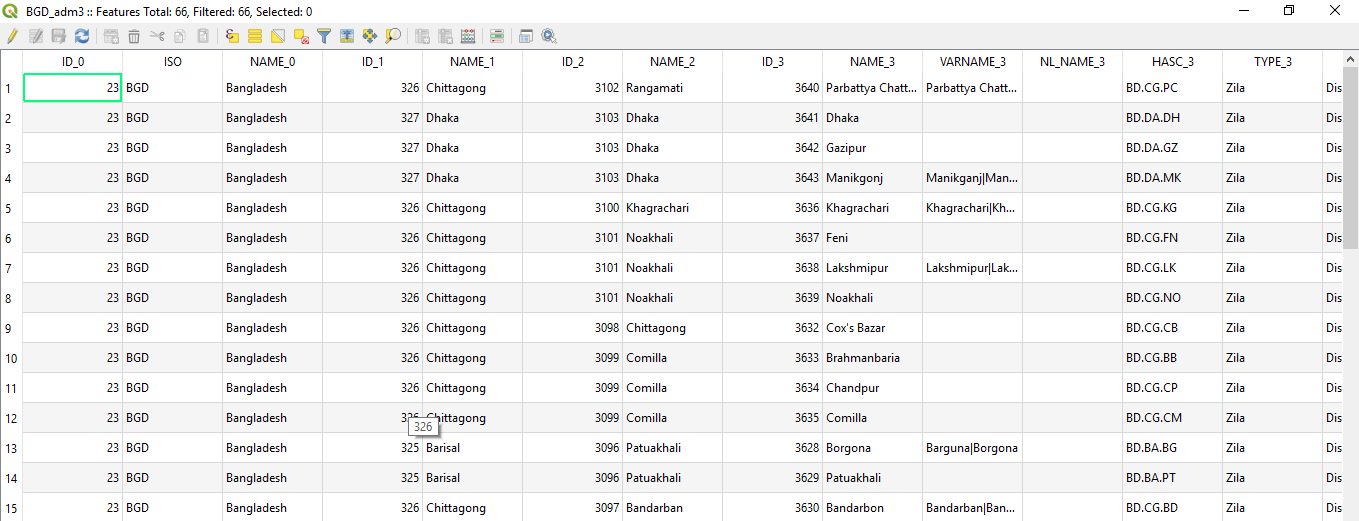
Similar to adding a vector layer, we can add a raster layer (or layers) and other database layer(s) to the QGIS environment, which we will look at more in-depth as we proceed further in this book.
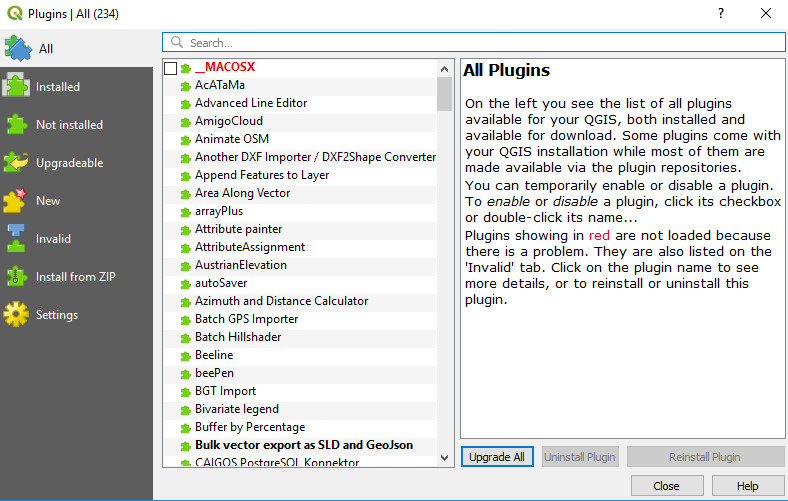
QGIS has a number of plugins that are add-ons that increase the functionality of QGIS. We can click on Plugin in the Menu Bar and then click on Manage and Install Plugins to install new plugins, as shown in this screenshot:

Now we will see a list of available plugins. Select the plugin you want to install, and then click on Install plugin. When the installation is finished, click Close:
In the next chapter, we will look at the basics of GIS and remote sensing (RS) and we will explore further how R and QGIS handle them and how we can use these two software for basic geospatial data loading and visualization.
Summary
In this chapter, we have learned how to download and install R and QGIS. We started with the installation of R, following which we also saw the various data types in R and how to work with these in R. Later in this chapter, we studied the programming aspects of R and also learned to use and apply loops and functions. Additionally, we saw how to visualize data in R using the ggplot2 package. Finally, we also learned about installing QGIS and also plugins, and we briefly studied the QGIS desktop.
We have only just scratched the surface of the many functionalities of R and QGIS. We have yet to touch upon working with spatial data, creating a spatial database, conducting spatial data analysis, and so on, which we will be introducing in Chapter 2, Fundamentals of GIS Using R and QGIS. Working with spatial data in R and QGIS requires us to know about the basics of GIS and how spatial data is being handled by R and QGIS, which we will be discussing in detail in Chapter 2. So, let's jump in!
Questions
If we have followed this chapter closely, by now, we should be able to answer the following questions:
- How do users install R?
- What are the basic data types in R?
- How can users work with these different types of data in R?
- How would users loop through a number of values in R?
- How would users write a function in R?
- What are lapply, sapply, and tapply and how are they used in R?
- How is data plotted in R?
- How do users install QGIS?
- How can users explore an attribute table in QGIS?
- How can users add vector (and raster) data in QGIS?
- How can users install plugins in QGIS?
Further reading
To get a good idea about the various aspects of data management and writing functions in R, please refer to R Cookbook by Paul Teetor and Advanced R by Hadley Wickham. If you are looking for a thorough introduction to QGIS, please refer to the books QGIS2 Cookbook by A Mandel et al and Mastering QGIS by K Menke et al.




















 Download code from GitHub
Download code from GitHub






