As you learned in the previous chapter, there are several entities in RL's view of the world:

• The agent: A thing, or person, that takes an active role. In practice, the agent is some piece of code that implements some policy. Basically, this policy decides what action is needed at every time step, given our observations.
• The environment: Some model of the world that is external to the agent and has the responsibility of providing observations and giving rewards. The environment changes its state based on the agent's actions.

Let's explore how both can be implemented in Python for a simple situation. We will define an environment that will give the agent random rewards for a limited number of steps, regardless of the agent's actions. This scenario is not very useful, but it will allow us to focus on specific methods in both the environment and agent classes. Let's start with the environment:

class Environment:
    def __init__(self):
        self.steps_left = 10

In the preceding code, we allowed the environment to initialize its internal state. In our case, the state is just a counter that limits the number of time steps that the agent is allowed to take to interact with the environment.

    def get_observation(self) -> List[float]:
        return [0.0, 0.0, 0.0]

The get_observation()method is supposed to return the current environment's observation to the agent. It is usually implemented as some function of the internal state of the environment. If you're curious about what is meant by-> List[float], that's an example of Python type annotations, which were introduced in Python 3.5. You can find out more in the documentation at https://docs.python.org/3/library/typing.html. In our example, the observation vector is always zero, as the environment basically has no internal state.

    def get_actions(self) -> List[int]:
        return [0, 1]

The get_actions() method allows the agent to query the set of actions it can execute. Normally, the set of actions that the agent can execute does not change over time, but some actions can become impossible in different states (for example, not every move is possible in any position of the tic-tac-toe game). In our simplistic example, there are only two actions that the agent can carry out, which are encoded with the integers 0 and 1.

    def is_done(self) -> bool:
        return self.steps_left == 0

The preceding method signaled the end of the episode to the agent. As you saw in Chapter 1, What Is Reinforcement Learning?, the series of environment-agent interactions is divided into a sequence of steps called episodes. Episodes can be finite, like in a game of chess, or infinite, like the Voyager 2 mission (a famous space probe that was launched over 40 years ago and has traveled beyond our solar system). To cover both scenarios, the environment provides us with a way to detect when an episode is over and there is no way to communicate with it anymore.

    def action(self, action: int) -> float:
        if self.is_done():
            raise Exception("Game is over")
        self.steps_left -= 1
        return random.random()

The action() method is the central piece in the environment's functionality. It does two things – handles an agent's action and returns the reward for this action. In our example, the reward is random and its action is discarded. Additionally, we update the count of steps and refuse to continue the episodes that are over.

Now when looking at the agent's part, it is much simpler and includes only two methods: the constructor and the method that performs one step in the environment:

class Agent:
    def __init__(self):
        self.total_reward = 0.0

In the constructor, we initialize the counter that will keep the total reward accumulated by the agent during the episode.

    def step(self, env: Environment):
        current_obs = env.get_observation()
        actions = env.get_actions()
        reward = env.action(random.choice(actions))
        self.total_reward += reward

The step function accepts the environment instance as an argument and allows the agent to perform the following actions:

• Observe the environment
• Make a decision about the action to take based on the observations
• Submit the action to the environment
• Get the reward for the current step

For our example, the agent is dull and ignores the observations obtained during the decision-making process about which action to take. Instead, every action is selected randomly. The final piece is the glue code, which creates both classes and runs one episode:

if __name__ == "__main__":
    env = Environment()
    agent = Agent()
    while not env.is_done():
        agent.step(env)
    print("Total reward got: %.4f" % agent.total_reward)

You can find the preceding code in this book's GitHub repository at https://github.com/PacktPublishing/Deep-Reinforcement-Learning-Hands-On-Second-Edition in the Chapter02/01_agent_anatomy.py file. It has no external dependencies and should work with any more-or-less modern Python version. By running it several times, you'll get different amounts of reward gathered by the agent.

The simplicity of the preceding code illustrates the important basic concepts that come from the RL model. The environment could be an extremely complicated physics model, and an agent could easily be a large neural network (NN) that implements the latest RL algorithm, but the basic pattern will stay the same – on every step, the agent will take some observations from the environment, do its calculations, and select the action to take. The result of this action will be a reward and a new observation.

You may ask, if the pattern is the same, why do we need to write it from scratch? What if it is already implemented by somebody and could be used as a library? Of course, such frameworks exist, but before we spend some time discussing them, let's prepare your development environment.

The examples in this book were implemented and tested using Python version 3.7. I assume that you're already familiar with the language and common concepts such as virtual environments, so I won't cover in detail how to install the package and how to do this in an isolated way. The examples will use the previously mentioned Python type annotations, which will allow us to provide type signatures for functions and class methods.

The external libraries that we will use in this book are open source software, and they include the following:

• NumPy: This is a library for scientific computing, and implementing matrix operations and common functions.
• OpenCV Python bindings: This is a computer vision library and provides many functions for image processing.
• Gym: This is an RL framework that has various environments that can be communicated with in a unified way.
• PyTorch: This is a flexible and expressive deep learning (DL) library. A short crash course on it will be given in Chapter 3, Deep Learning with PyTorch.
• PyTorch Ignite: This is a set of high-level tools on top of PyTorch used to reduce boilerplate code. It will be covered briefly in Chapter 3. The full documentation is available here: https://pytorch.org/ignite/.
• PTAN (https://github.com/Shmuma/ptan): This is an open source extension to Gym that I created to support the modern deep RL methods and building blocks. All classes used will be described in detail together with the source code.

Other libraries will be used for specific chapters; for example, we will use Microsoft TextWorld for solving text-based games, PyBullet for robotic simulations, OpenAI Universe for browser-based automation problems, and so on. Those specialized chapters will include installation instructions for those libraries.

A significant portion of this book (parts two, three, and four) is focused on the modern deep RL methods that have been developed over the past few years. The word "deep" in this context means that DL is heavily used. You may be aware that DL methods are computationally hungry. One modern graphics processing unit (GPU) can be 10 to 100 times faster than even the fastest multiple central processing unit (CPU) systems. In practice, this means that the same code that takes one hour to train on a system with a GPU could take from half a day to one week even on the fastest CPU system. It doesn't mean that you can't try the examples from this book without having access to a GPU, but it will take longer. To experiment with the code on your own (the most useful way to learn anything), it is better to get access to a machine with a GPU. This can be done in various ways:

• Buying a modern GPU suitable for CUDA
• Using cloud instances. Both Amazon Web Services and Google Cloud can provide you with GPU-powered instances
• Google Colab offers free GPU access to its Jupyter notebooks

The instructions on how to set up the system are beyond the scope of this book, but there are plenty of manuals available on the Internet. In terms of an operating system (OS), you should use Linux or macOS. Windows is supported by PyTorch and Gym, but the examples in the book were not fully tested under Windows OS.

To give you the exact versions of the external dependencies that we will use throughout the book, here is an output of the pip freeze command (it may be useful for the potential troubleshooting of examples in the book, as open source software and DL toolkits are evolving extremely quickly):

atari-py==0.2.6
gym==0.15.3
numpy==1.17.2
opencv-python==4.1.1.26
tensorboard==2.0.1
torch==1.3.0
torchvision==0.4.1
pytorch-ignite==0.2.1
tensorboardX==1.9
tensorflow==2.0.0
ptan==0.6

All the examples in the book were written and tested with PyTorch 1.3, which can be installed by following the instructions on the http://pytorch.org website (normally, that's just the conda install pytorch torchvision -c pytorch command).

Now, let's go into the details of the OpenAI Gym API, which provides us with tons of environments, from trivial to challenging ones.

The Python library called Gym was developed and has been maintained by OpenAI (www.openai.com). The main goal of Gym is to provide a rich collection of environments for RL experiments using a unified interface. So, it is not surprising that the central class in the library is an environment, which is called Env. Instances of this class expose several methods and fields that provide the required information about its capabilities. At a high level, every environment provides these pieces of information and functionality:

• A set of actions that is allowed to be executed in the environment. Gym supports both discrete and continuous actions, as well as their combination
• The shape and boundaries of the observations that the environment provides the agent with
• A method called step to execute an action, which returns the current observation, the reward, and the indication that the episode is over
• A method called reset, which returns the environment to its initial state and obtains the first observation

Let's now talk about these components of the environment in detail.

The action space

As mentioned, the actions that an agent can execute can be discrete, continuous, or a combination of the two. Discrete actions are a fixed set of things that an agent can do, for example, directions in a grid like left, right, up, or down. Another example is a push button, which could be either pressed or released. Both states are mutually exclusive, because a main characteristic of a discrete action space is that only one action from a finite set of actions is possible.

A continuous action has a value attached to it, for example, a steering wheel, which can be turned at a specific angle, or an accelerator pedal, which can be pressed with different levels of force. A description of a continuous action includes the boundaries of the value that the action could have. In the case of a steering wheel, it could be from −720 degrees to 720 degrees. For an accelerator pedal, it's usually from 0 to 1.

Of course, we are not limited to a single action; the environment could take multiple actions, such as pushing multiple buttons simultaneously or steering the wheel and pressing two pedals (the brake and the accelerator). To support such cases, Gym defines a special container class that allows the nesting of several action spaces into one unified action.

The observation space

As mentioned in Chapter 1, What Is Reinforcement Learning?, observations are pieces of information that an environment provides the agent with, on every timestamp, besides the reward. Observations can be as simple as a bunch of numbers or as complex as several multidimensional tensors containing color images from several cameras. An observation can even be discrete, much like action spaces. An example of a discrete observation space is a lightbulb, which could be in two states – on or off, given to us as a Boolean value.

So, you can see the similarity between actions and observations, and how they have found their representation in Gym's classes. Let's look at a class diagram:

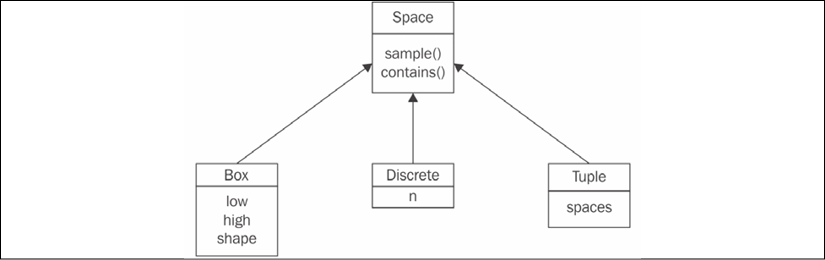
Figure 2.1: The hierarchy of the Space class in Gym

The basic abstract class Space includes two methods that are relevant to us:

• sample(): This returns a random sample from the space
• contains(x): This checks whether the argument, x, belongs to the space's domain

Both of these methods are abstract and reimplemented in each of the Space subclasses:

• The Discrete class represents a mutually exclusive set of items, numbered from 0 to n – 1. Its only field, n, is a count of the items it describes. For example, Discrete(n=4) can be used for an action space of four directions to move in [left, right, up, or down].
• The Box class represents an n-dimensional tensor of rational numbers with intervals [low, high]. For instance, this could be an accelerator pedal with one single value between 0.0 and 1.0, which could be encoded by Box(low=0.0, high=1.0, shape=(1,), dtype=np.float32)(the shape argument is assigned a tuple of length 1 with a single value of 1, which gives us a one-dimensional tensor with a single value). The dtype parameter specifies the space's value type and here we specify it as a NumPy 32-bit float. Another example of Box could be an Atari screen observation (we will cover lots of Atari environments later), which is an RGB (red, green, and blue) image of size 210×160: Box(low=0, high=255, shape=(210, 160, 3), dtype=np.uint8). In this case, the shape argument is a tuple of three elements: the first dimension is the height of the image, the second is the width, and the third equals 3, which all correspond to three color planes for red, green, and blue, respectively. So, in total, every observation is a three-dimensional tensor with 100,800 bytes.
• The final child of Space is a Tuple class, which allows us to combine several Space class instances together. This enables us to create action and observation spaces of any complexity that we want. For example, imagine we want to create an action space specification for a car. The car has several controls that can be changed at every timestamp, including the steering wheel angle, brake pedal position, and accelerator pedal position. These three controls can be specified by three float values in one single Box instance. Besides these essential controls, the car has extra discrete controls, like a turn signal (which could be off, right, or left) or horn (on or off). To combine all of this into one action space specification class, we can create Tuple(spaces=(Box(low=-1.0, high=1.0, shape=(3,), dtype=np.float32), Discrete(n=3),Discrete(n=2))). This flexibility is rarely used; for example, in this book, you will see only the Box and Discrete actions and observation spaces, but the Tuple class can be useful in some cases.

There are other Space subclasses defined in Gym, but the preceding three are the most useful ones. All subclasses implement the sample() and contains() methods. The sample() function performs a random sample corresponding to the Space class and parameters. This is mostly useful for action spaces, when we need to choose the random action. The contains() method verifies that the given arguments comply with the Space parameters, and it is used in the internals of Gym to check an agent's actions for sanity. For example, Discrete.sample() returns a random element from a discrete range, and Box.sample() will be a random tensor with proper dimensions and values lying inside the given range.

Every environment has two members of type Space: the action_space and observation_space. This allows us to create generic code that could work with any environment. Of course, dealing with the pixels of the screen is different from handling discrete observations (as in the former case, we may want to preprocess images with convolutional layers or with other methods from the computer vision toolbox); so, most of the time, this means optimizing the code for a particular environment or group of environments, but Gym doesn't prevent us from writing generic code.

The environment

The environment is represented in Gym by the Env class, as mentioned earlier, which has the following members:

• action_space: This is the field of the Space class and provides a specification for allowed actions in the environment.
• observation_space: This field has the same Space class, but specifies the observations provided by the environment.
• reset(): This resets the environment to its initial state, returning the initial observation vector.
• step(): This method allows the agent to take the action and returns information about the outcome of the action – the next observation, the local reward, and the end-of-episode flag. This method is a bit complicated and we we will look at it in detail later in this section.

There are extra utility methods in the Env class, such as render(), which allows us to obtain the observation in a human-friendly form, but we won't use them. You can find the full list in Gym's documentation, but let's focus on the core Env methods: reset() and step().

So far, you have seen how our code can get information about the environment's actions and observations, so now you need to get familiar with actioning itself. Communications with the environment are performed via step and reset.

As reset is much simpler, we will start with it. The reset() method has no arguments; it instructs an environment to reset into its initial state and obtain the initial observation. Note that you have to call reset() after the creation of the environment. As you may remember from Chapter 1, What Is Reinforcement Learning?, the agent's communication with the environment may have an end (like a "Game Over" screen). Such sessions are called episodes, and after the end of the episode, an agent needs to start over. The value returned by this method is the first observation of the environment.

The step() method is the central piece in the environment's functionality. It does several things in one call, which are as follows:

• Telling the environment which action we will execute on the next step
• Getting the new observation from the environment after this action
• Getting the reward the agent gained with this step
• Getting the indication that the episode is over

The first item (action) is passed as the only argument to this method, and the rest are returned by the step() method. Precisely, this is a tuple (Python tuple and not the Tuple class we discussed in the previous section) of four elements (observation, reward, done, and info). They have these types and meanings:

• observation: This is a NumPy vector or a matrix with observation data.
• reward: This is the float value of the reward.
• done: This is a Boolean indicator, which is True when the episode is over.
• info: This could be anything environment-specific with extra information about the environment. The usual practice is to ignore this value in general RL methods (not taking into account the specific details of the particular environment).

You may have already got the idea of environment usage in an agent's code – in a loop, we call the step() method with an action to perform until this method's done flag becomes True. Then we can call reset() to start over. There is only one piece missing – how we create Env objects in the first place.

Creating an environment

Every environment has a unique name of the EnvironmentName-vN form, where N is the number used to distinguish between different versions of the same environment (when, for example, some bugs get fixed or some other major changes are made). To create an environment, the gym package provides the make(env_name) function, whose only argument is the environment's name in string form.

At the time of writing, Gym version 0.13.1 contains 859 environments with different names. Of course, all of those are not unique environments, as this list includes all versions of an environment. Additionally, the same environment can have different variations in the settings and observations spaces. For example, the Atari game Breakout has these environment names:

• Breakout-v0, Breakout-v4: The original Breakout with a random initial position and direction of the ball
• BreakoutDeterministic-v0, BreakoutDeterministic-v4: Breakout with the same initial placement and speed vector of the ball
• BreakoutNoFrameskip-v0, BreakoutNoFrameskip-v4: Breakout with every frame displayed to the agent
• Breakout-ram-v0, Breakout-ram-v4: Breakout with the observation of the full Atari emulation memory (128 bytes) instead of screen pixels
• Breakout-ramDeterministic-v0, Breakout-ramDeterministic-v4
• Breakout-ramNoFrameskip-v0, Breakout-ramNoFrameskip-v4

In total, there are 12 environments for good old Breakout. In case you've never seen it before, here is a screenshot of its gameplay:

Figure 2.2: The gameplay of Breakout

Even after the removal of such duplicates, Gym 0.13.1 comes with an impressive list of 154 unique environments, which can be divided into several groups:

• Classic control problems: These are toy tasks that are used in optimal control theory and RL papers as benchmarks or demonstrations. They are usually simple, with low-dimension observation and action spaces, but they are useful as quick checks when implementing algorithms. Think about them as the "MNIST for RL" (MNIST is a handwriting digit recognition dataset from Yann LeCun, which you can find at http://yann.lecun.com/exdb/mnist/).
• Atari 2600: These are games from the classic game platform from the 1970s. There are 63 unique games.
• Algorithmic: These are problems that aim to perform small computation tasks, such as copying the observed sequence or adding numbers.
• Board games: These are the games of Go and Hex.
• Box2D: These are environments that use the Box2D physics simulator to learn walking or car control.
• MuJoCo: This is another physics simulator used for several continuous control problems.
• Parameter tuning: This is RL being used to optimize NN parameters.
• Toy text: These are simple grid world text environments.
• PyGame: These are several environments implemented using the PyGame engine.
• Doom: These are nine mini-games implemented on top of ViZDoom.

The full list of environments can be found at https://gym.openai.com/envs or on the wiki page in the project's GitHub repository. An even larger set of environments is available in OpenAI Universe (currently discontinued by OpenAI), which provides general connectors to virtual machines while running Flash and native games, web browsers, and other real-world applications. OpenAI Universe extends the Gym API, but it follows the same design principles and paradigm. You can check it out at https://github.com/openai/universe. We will deal with Universe more closely in Chapter 13, Asynchronous Advantage Actor-Critic, in terms of MiniWoB and browser automation.

Enough theory! Let's now look at a Python session working with one of Gym's environments.

The CartPole session

Let's apply our knowledge and explore one of the simplest RL environments that Gym provides.

$ python
Python 3.7.5 |Anaconda, Inc.| (default, Mar 29 2018, 18:21:58)
[GCC 7.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import gym
>>> e = gym.make('CartPole-v0')

Here, we have imported the gym package and created an environment called CartPole. This environment is from the classic control group and its gist is to control the platform with a stick attached by its bottom part (see the following figure).

The trickiness is that this stick tends to fall right or left and you need to balance it by moving the platform to the right or left on every step.

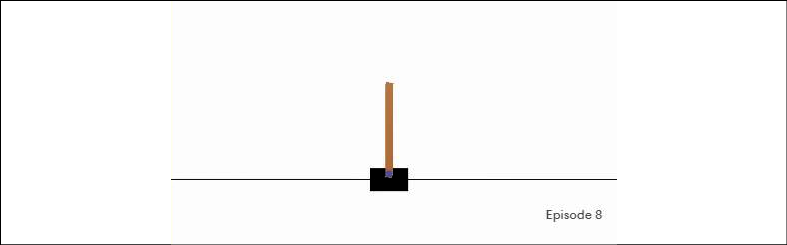
Figure 2.3: The CartPole environment

The observation of this environment is four floating-point numbers containing information about the x coordinate of the stick's center of mass, its speed, its angle to the platform, and its angular speed. Of course, by applying some math and physics knowledge, it won't be complicated to convert these numbers into actions when we need to balance the stick, but our problem is this – how do we learn to balance this system without knowing the exact meaning of the observed numbers and only by getting the reward? The reward in this environment is 1, and it is given on every time step. The episode continues until the stick falls, so to get a more accumulated reward, we need to balance the platform in a way to avoid the stick falling.

This problem may look difficult, but in just two chapters, we will write the algorithm that will easily solve CartPole in minutes, without any idea about what the observed numbers mean. We will do it only by trial and error and using a bit of RL magic.

Let's continue with our session.

>>> obs = e.reset()
>>> obs
array([-0.04937814, -0.0266909 , -0.03681807, -0.00468688])

Here, we reset the environment and obtained the first observation (we always need to reset the newly created environment). As I said, the observation is four numbers, so let's check how we can know this in advance.

>>> e.action_space
Discrete(2)
>>> e.observation_space
Box(4,)

The action_space field is of the Discrete type, so our actions will be just 0 or 1, where 0 means pushing the platform to the left and 1 means to the right. The observation space is of Box(4,), which means a vector of size 4 with values inside the [−inf, inf] interval.

>>> e.step(0)
(array([-0.04991196, -0.22126602, -0.03691181, 0.27615592]), 1.0,
False, {})

Here, we pushed our platform to the left by executing the action 0 and got the tuple of four elements:

• A new observation, which is a new vector of four numbers
• A reward of 1.0
• The done flag with value False, which means that the episode is not over yet and we are more or less okay
• Extra information about the environment, which is an empty dictionary

Next, we will use the sample() method of the Space class on the action_space and observation_space.

>>> e.action_space.sample()
0
>>> e.action_space.sample()
1
>>> e.observation_space.sample()
array([2.06581792e+00, 6.99371255e+37, 3.76012475e-02,
-5.19578481e+37])
>>> e.observation_space.sample()
array([4.6860966e-01, 1.4645028e+38, 8.6090848e-02, 3.0545910e+37])

This method returned a random sample from the underlying space, which in the case of our Discrete action space means a random number of 0 or 1, and for the observation space means a random vector of four numbers. The random sample of the observation space may not look useful, and this is true, but the sample from the action space could be used when we are not sure how to perform an action. This feature is especially handy because you don't know any RL methods yet, but we still want to play around with the Gym environment. Now that you know enough to implement your first randomly behaving agent for CartPole, let's do it.

Although the environment is much more complex than our first example in The anatomy of the agent section, the code of the agent is much shorter. This is the power of reusability, abstractions, and third-party libraries!

So, here is the code (you can find it in Chapter02/02_cartpole_random.py).

import gym
if __name__ == "__main__":
    env = gym.make("CartPole-v0")
    total_reward = 0.0
    total_steps = 0
    obs = env.reset()

Here, we created the environment and initialized the counter of steps and the reward accumulator. On the last line, we reset the environment to obtain the first observation (which we will not use, as our agent is stochastic).

    while True:
        action = env.action_space.sample()
        obs, reward, done, _ = env.step(action)
        total_reward += reward
        total_steps += 1
        if done:
            break
    print("Episode done in %d steps, total reward %.2f" % (
        total_steps, total_reward))

In this loop, we sampled a random action, then asked the environment to execute it and return to us the next observation (obs), the reward, and the done flag. If the episode is over, we stop the loop and show how many steps we have taken and how much reward has been accumulated. If you start this example, you will see something like this (not exactly, though, due to the agent's randomness):

rl_book_samples/Chapter02$ python 02_cartpole_random.py
Episode done in 12 steps, total reward 12.00

As with the interactive session, the warning is not related to our code, but to Gym's internals. On average, our random agent takes 12 to 15 steps before the pole falls and the episode ends. Most of the environments in Gym have a "reward boundary," which is the average reward that the agent should gain during 100 consecutive episodes to "solve" the environment. For CartPole, this boundary is 195, which means that, on average, the agent must hold the stick for 195 time steps or longer. Using this perspective, our random agent's performance looks poor. However, don't be disappointed; we are just at the beginning, and soon you will solve CartPole and many other much more interesting and challenging environments.

What we have discussed so far covers two-thirds of the Gym core API and the essential functions required to start writing agents. The rest of the API you can live without, but it will make your life easier and your code cleaner. So, let's briefly cover the rest of the API.

Wrappers

Very frequently, you will want to extend the environment's functionality in some generic way. For example, imagine an environment gives you some observations, but you want to accumulate them in some buffer and provide to the agent the N last observations. This is a common scenario for dynamic computer games, when one single frame is just not enough to get the full information about the game state. Another example is when you want to be able to crop or preprocess an image's pixels to make it more convenient for the agent to digest, or if you want to normalize reward scores somehow. There are many such situations that have the same structure – you want to "wrap" the existing environment and add some extra logic for doing something. Gym provides a convenient framework for these situations – the Wrapper class.

The class structure is shown in the following diagram.

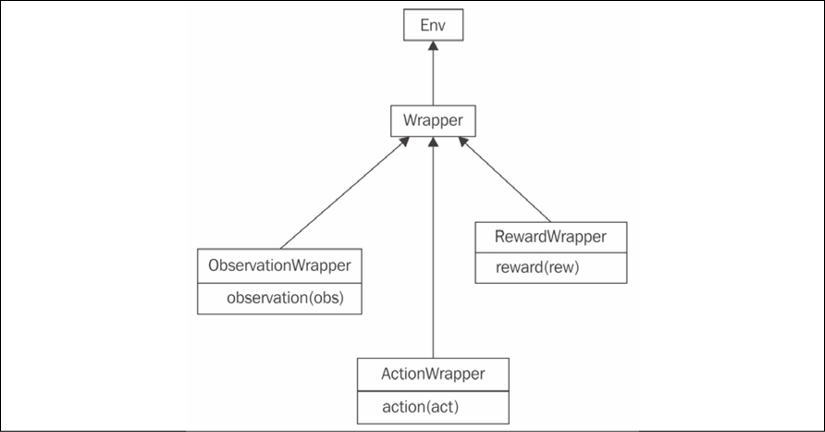
Figure 2.4: The hierarchy of Wrapper classes in Gym

The Wrapper class inherits the Env class. Its constructor accepts the only argument – the instance of the Env class to be "wrapped." To add extra functionality, you need to redefine the methods you want to extend, such as step() or reset(). The only requirement is to call the original method of the superclass.

To handle more specific requirements, such as a Wrapper class that wants to process only observations from the environment, or only actions, there are subclasses of Wrapper that allow the filtering of only a specific portion of information. They are as follows:

• ObservationWrapper: You need to redefine the observation (obs) method of the parent. The obs argument is an observation from the wrapped environment, and this method should return the observation that will be given to the agent.
• RewardWrapper: This exposes the reward (rew) method, which can modify the reward value given to the agent.
• ActionWrapper: You need to override the action (act) method, which can tweak the action passed to the wrapped environment by the agent.

To make it slightly more practical, let's imagine a situation where we want to intervene in the stream of actions sent by the agent and, with a probability of 10%, replace the current action with a random one. It might look like an unwise thing to do, but this simple trick is one of the most practical and powerful methods for solving the exploration/exploitation problem that I mentioned briefly in Chapter 1, What Is Reinforcement Learning?. By issuing the random actions, we make our agent explore the environment and from time to time drift away from the beaten track of its policy. This is an easy thing to do using the ActionWrapper class (a full example is in Chapter02/03_random_action_wrapper.py).

import gym
from typing import TypeVar
import random
Action = TypeVar('Action')
class RandomActionWrapper(gym.ActionWrapper):
    def __init__(self, env, epsilon=0.1):
        super(RandomActionWrapper, self).__init__(env)
        self.epsilon = epsilon

Here, we initialized our wrapper by calling a parent's __init__ method and saving epsilon (the probability of a random action).

    def action(self, action: Action) -> Action:
        if random.random() < self.epsilon:
            print("Random!")
            return self.env.action_space.sample()
        return action

This is a method that we need to override from a parent's class to tweak the agent's actions. Every time we roll the die, and with the probability of epsilon, we sample a random action from the action space and return it instead of the action the agent has sent to us. Note that using action_space and wrapper abstractions, we were able to write abstract code, which will work with any environment from Gym. Additionally, we must print the message every time we replace the action, just to verify that our wrapper is working. In the production code, of course, this won't be necessary.

if __name__ == "__main__":
    env = RandomActionWrapper(gym.make("CartPole-v0"))

Now it's time to apply our wrapper. We will create a normal CartPole environment and pass it to our Wrapper constructor. From here on, we will use our wrapper as a normal Env instance, instead of the original CartPole. As the Wrapper class inherits the Env class and exposes the same interface, we can nest our wrappers in any combination we want. This is a powerful, elegant, and generic solution.

    obs = env.reset()
    total_reward = 0.0
    while True:
        obs, reward, done, _ = env.step(0)
        total_reward += reward
        if done:
            break
    print("Reward got: %.2f" % total_reward)

Here is almost the same code, except that every time we issue the same action, 0, our agent is dull and does the same thing. By running the code, you should see that the wrapper is indeed working.

rl_book_samples/Chapter02$ python 03_random_actionwrapper.py
Random!
Random!
Random!
Random!
Reward got: 12.00

If you want, you can play with the epsilon parameter on the wrapper's creation and verify that randomness improves the agent's score on average.

We should move on now and look at another interesting gem that is hidden inside Gym: Monitor.

Monitor

Another class that you should be aware of is Monitor. It is implemented like Wrapper and can write information about your agent's performance in a file, with an optional video recording of your agent in action. Some time ago, it was possible to upload the result of the Monitor class' recording to the https://gym.openai.com website and see your agent's position in comparison to other people's results (see the following screenshot), but, unfortunately, at the end of August 2017, OpenAI decided to shut down this upload functionality and froze all the results. There are several alternatives to the original website, but they are not ready yet. I hope this situation will be resolved soon, but at the time of writing, it is not possible to check your results against those of others.

Just to give you an idea of how the Gym web interface looked, here is the CartPole environment leaderboard:

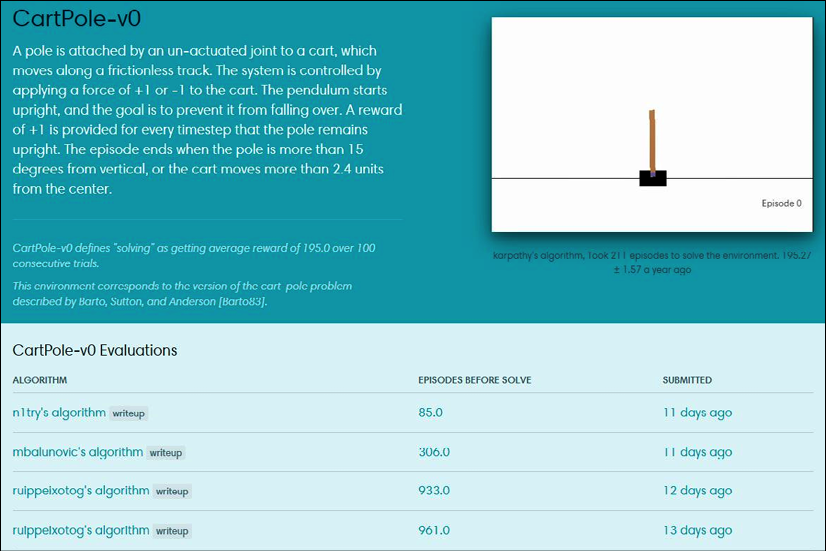
Figure 2.5: The Gym web interface with CartPole submissions

Every submission in the web interface had details about training dynamics. For example, the following is my solution for one of Doom's mini-games:

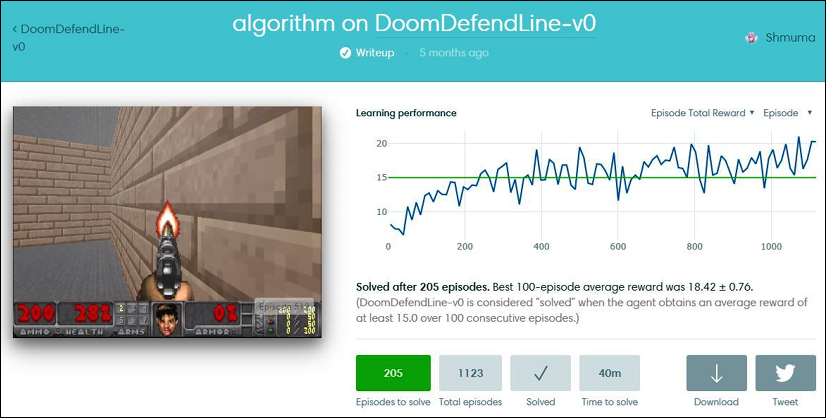
Figure 2.6: Submission dynamics for the DoomDefendLine environment

Despite this, Monitor is still useful, as you can take a look at your agent's life inside the environment. So, here is how we add Monitor to our random CartPole agent, which is the only difference (the entire code is in Chapter02/04_cartpole_random_monitor.py).

if __name__ == "__main__":
    env = gym.make("CartPole-v0")
    env = gym.wrappers.Monitor(env, "recording")

The second argument that we pass to Monitor is the name of the directory that it will write the results to. This directory shouldn't exist, otherwise your program will fail with an exception (to overcome this, you could either remove the existing directory or pass the force=True argument to the Monitor class' constructor).

The Monitor class requires the FFmpeg utility to be present on the system, which is used to convert captured observations into an output video file. This utility must be available, otherwise Monitor will raise an exception. The easiest way to install FFmpeg is using your system's package manager, which is OS distribution-specific.

To start this example, one of these three extra prerequisites should be met:

• The code should be run in an X11 session with the OpenGL extension (GLX)
• The code should be started in an Xvfb virtual display
• You can use X11 forwarding in an SSH connection

The reason for this is video recording, which is done by taking screenshots of the window drawn by the environment. Some of the environment uses OpenGL to draw its picture, so the graphical mode with OpenGL needs to be present. This could be a problem for a virtual machine in the cloud, which physically doesn't have a monitor and graphical interface running. To overcome this, there is a special "virtual" graphical display, called Xvfb (X11 virtual framebuffer), which basically starts a virtual graphical display on the server and forces the program to draw inside it. This would be enough to make Monitor happily create the desired videos.

To start your program in the Xvfb environment, you need to have it installed on your machine (this usually requires installing the xvfb package) and run the special script, xvfb-run:

$ xvfb-run -s "-screen 0 640x480x24" python 04_cartpole_random_monitor.py [2017-09-22 12:22:23,446] Making new env: CartPole-v0
[2017-09-22 12:22:23,451] Creating monitor directory recording
[2017-09-22 12:22:23,570] Starting new video recorder writing to recording/openaigym.video.0.31179.video000000.mp4
Episode done in 14 steps, total reward 14.00
[2017-09-22 12:22:26,290] Finished writing results. You can upload them to the scoreboard via gym.upload('recording')

As you may see from the preceding log, the video has been written successfully, so you can peek inside one of your agent's sections by playing it.

Another way to record your agent's actions is to use SSH X11 forwarding, which uses the SSH ability to tunnel X11 communications between the X11 client (Python code that wants to display some graphical information) and X11 server (software that knows how to display this information and has access to your physical display).

In X11 architecture, the client and the server are separated and can work on different machines. To use this approach, you need the following:

1. An X11 server running on your local machine. Linux comes with an X11 server as a standard component (all desktop environments use X11). On a Windows machine, you can set up third-party X11 implementations, such as open source VcXsrv (available in https://sourceforge.net/projects/vcxsrv/).
2. The ability to log into your remote machine via SSH, passing the –X command-line option: ssh –X servername. This enables X11 tunneling and allows all processes started in this session to use your local display for graphics output.

Then, you can start a program that uses the Monitor class and it will display the agent's actions, capturing the images in a video file.