Deep Neural Networks
In this chapter, we'll be examining deep neural networks. These networks have shown excellent performance in terms of the accuracy of their classification on more challenging datasets like ImageNet, CIFAR10 (https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf), and CIFAR100. For conciseness, we'll only be focusing on two networks: ResNet [2][4] and DenseNet [5]. While we will go into much more detail, it's important to take a minute to introduce these networks.
ResNet introduced the concept of residual learning, which enabled it to build very deep networks by addressing the vanishing gradient problem (discussed in section 2) in deep convolutional networks.
DenseNet improved ResNet further by allowing every convolution to have direct access to inputs, and lower layer feature maps. It's also managed to keep the number of parameters low in deep networks by utilizing both the Bottleneck and Transition layers...
1. Functional API
In the Sequential model API that we first introduced in Chapter 1, Introducing Advanced Deep Learning with Keras, a layer is stacked on top of another layer. Generally, the model will be accessed through its input and output layers. We also learned that there is no simple mechanism if we find ourselves wanting to add an auxiliary input at the middle of the network, or even to extract an auxiliary output before the last layer.
That model also had its downsides; for example, it doesn't support graph-like models or models that behave like Python functions. In addition, it's also difficult to share layers between the two models. Such limitations are addressed by the Functional API and are the reason why it's a vital tool for anyone wanting to work with deep learning models.
The Functional API is guided by the following two concepts:
2. Deep Residual Network (ResNet)
One key advantage of deep networks is that they have a great ability to learn different levels of representation from both inputs and feature maps. In classification, segmentation, detection, and a number of other computer vision problems, learning different feature maps generally leads to a better performance.
However, you'll find that it's not easy to train deep networks because the gradient may vanish (or explode) with depth in the shallow layers during backpropagation. Figure 2.2.1 illustrates the problem of vanishing gradient. The network parameters are updated by backpropagation from the output layer to all previous layers. Since backpropagation is based on the chain rule, there is a tendency for the gradient to diminish as it reaches the shallow layers. This is due to the multiplication of small numbers, especially for small loss functions and parameter values.
The number of multiplication operations will be proportional to...
3. ResNet v2
The improvements for ResNet v2 are mainly found in the arrangement of layers in the residual block as shown in Figure 2.3.1.
The prominent changes in ResNet v2 are:
- The use of a stack of 1 x 1 – 3 x 3 – 1 × 1
BN-ReLU-Conv2D - Batch normalization and ReLU activation come before two dimensional convolution

Figure 2.3.1: A comparison of residual blocks between ResNet v1 and ResNet v2
ResNet v2 is also implemented in the same code as resnet-cifar10-2.2.1.py, as can be seen in Listing 2.2.1:
Listing 2.2.1: resnet-cifar10-2.2.1.py
def resnet_v2(input_shape, depth, num_classes=10):
"""ResNet Version 2 Model builder [b]
Stacks of (1 x 1)-(3 x 3)-(1 x 1) BN-ReLU-Conv2D or
also known as bottleneck layer.
First shortcut connection per layer is 1 x 1 Conv2D.
Second and onwards shortcut connection is identity.
At the beginning of each stage,
the feature map size...4. Densely Connected Convolutional Network (DenseNet)
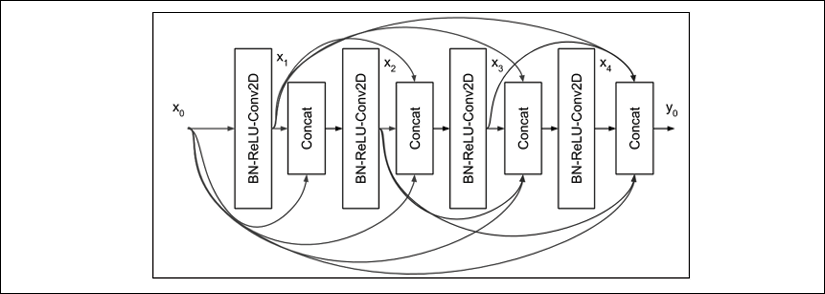
Figure 2.4.1: A 4-layer Dense block in DenseNet.The input to each layer is made of all the previous feature maps.
DenseNet attacks the problem of vanishing gradient using a different approach. Instead of using shortcut connections, all the previous feature maps will become the input of the next layer. The preceding figure shows an example of a Dense interconnection in one Dense block.
For simplicity, in this figure, we'll only show four layers. Notice that the input to layer l is the concatenation of all previous feature maps. If we let BN-ReLU-Conv2D be represented by the operation H(x), then the output of layer l is:
xl = H (x0,x1,x2, ,xl-1) (Equation 2.4.1)
Conv2D uses a kernel of size 3. The number of feature maps generated per layer is called the growth rate, k. Normally, k = 12, but k = 24 is also used in the paper Densely Connected Convolutional Networks by Huang et al. (2017) [5]. Therefore...
5. Conclusion
In this chapter, we've presented the Functional API as an advanced method for building complex deep neural network models using tf.keras. We also demonstrated how the Functional API could be used to build the multi-input-single-output Y-Network. This network, when compared to a single branch CNN network, achieves better accuracy. For the rest of the book, we'll find the Functional API indispensable in building more complex and advanced models. For example, in the next chapter, the Functional API will enable us to build a modular encoder, decoder, and autoencoder.
We also spent a significant amount of time exploring two important deep networks, ResNet and DenseNet. Both of these networks have been used not only in classification but also in other areas, such as segmentation, detection, tracking, generation, and visual semantic understanding. In Chapter 11, Object Detection, and Chapter 12, Semantic Segmentation, we will use ResNet for object detection and...
6. References
- Kaiming He et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. Proceedings of the IEEE international conference on computer vision, 2015 (https://www.cv-foundation.org/openaccess/content_iccv_2015/papers/He_Delving_Deep_into_ICCV_2015_paper.pdfspm=5176.100239.blogcont55892.28.pm8zm1&file=He_Delving_Deep_into_ICCV_2015_paper.pdf).
- Kaiming He et al. Deep Residual Learning for Image Recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016a (http://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf).
- Karen Simonyan and Andrew Zisserman. Very Deep Convolutional Networks for Large-Scale Image Recognition. ICLR, 2015 (https://arxiv.org/pdf/1409.1556/).
- Kaiming He et al. Identity Mappings in Deep Residual Networks. European Conference on Computer Vision. Springer International Publishing, 2016b (https://arxiv.org/pdf/1603...




















 Download code from GitHub
Download code from GitHub






